Навигация
Навести приклад наближеної моделі об’єкту дослідження на мікрорівні
7. Навести приклад наближеної моделі об’єкту дослідження на мікрорівні
Точне рішення крайових задач вдається одержати лише для деяких окремих випадків. Тому загальний спосіб їхнього рішення полягає у використанні різних наближених моделей. В даний час найбільш широке поширення одержали моделі на основі інтегральних рівнянь і моделі на основі методу сіток.
Основна ідея побудови моделі на основі інтегральних рівнянь полягає в переході від вихідного диференціального рівняння в часткових похідних до еквівалентного інтегрального рівняння, що підлягає подальшим перетворенням.
Сутність методу сіток складається в апроксимації шуканої безперервної функції сукупністю наближених значень, розрахованих у деяких точках області - вузлах. Сукупність вузлів, з'єднаних певним чином, утворить сітку. Сітка, у свою чергу, є дискретною моделлю області визначення шуканої функції.
Застосування методу сіток дозволяє звести диференціальну крайову задачу до системи нелінійних у загальному випадку алгебраїчних рівнянь щодо невідомих вузлових значень функцій.
У загальному випадку алгоритм методу сіток складається з трьох етапів.
Етап 1. Побудова сітки в заданій області (дискретизація задачі).
Етап 2. Одержання системи алгебраїчних рівнянь щодо вузлових значень (алгебраізація задачі).
Етап 3. Рішення отриманої системи алгебраїчних рівнянь.
Найбільше часто використовуються два методи сіток: 1) метод кінцевих елементів (МКЕ); 2) метод кінцевих різностей (МКР). Ці методи відрізняються один від одного на етапах 1 і 2 алгоритму. На етапі 3 методи практично ідентичні.
8. Розглянути аналогії топологічних рівнянь
Складання топологічної матриціДля формування рівнянь слід скласти топологічну матрицю F, яка називається матрицею "контур-вітка". Ця матриця відображає структуру так званих особливих контурів. Особливий контур утворюється, якщо до дерева додати тільки один зв’язок. При цьому в отриманому контурі напрямок цього зв’зку вказує позитивний напрямок для цього особливого контура. Якщо при обході контура за цим позитивним напрямком вітка співпадає, то вона дає в стрічку матриці позитивну одиницю. Якщо напрямок вітки протилежний позитивному напрямку в контурі, то в стрічці повинна бути записана від’ємна одиниця. Якщо вітка не входить до особливого контура, то в матриці цьому елементу відповідає нульовий елемент, при цьому нулі можна не вписувати в матрицю, залишаючи ці клітки матриці пустими. Стрічки топологічної матриці відповідають зв’язкам, а стовпці відображають вітки графа електричної системи. Тому кількість стрічок у топологічній матриці повинна дорівнювати кількості зв’язків, а кількість стовпців - кількості віток. Рекомендується розташовувати стовпці й стрічки топологічної матриці відповідно до порядку E-C-R-L-J, що приймається при виборі дерева, і відповідні назви ребер елементів надписувати над кожним стовпцем і зліва біля кожної стрічки.
Топологічні рівняння у матричній форміТопологічні рівняння електричної системи складають у матричній формі за рівняннями Кірхгофа. Для цього слід скласти чотири вектори (матриці-стовпці) для струмів і напруг віток та зв’язків:
Vв -вектор напруг на вітках графа;
Vс -вектор напруг на зв’язках;
Iв -вектор струмів на вітках графа;
Iс -вектор струмів на зв’язках.
Тепер система топологічних рівнянь в матричній формі може бути подана у вигляді таких рівнянь:
Vс = -FVв ;
Iв = FтIс .
Перше рівняння відображає контурні рівняння для напруг, що складаються для системи особливих контурів. Друге рівняння відображає рівняння для струмів для системи особливих розрізів. Під розрізом розуміють сукупність ребер, при розриві яких граф розпадається на дві окремі частини, однією з яких може бути навіть окремий вузол - в цьому разі такий розріз називається канонічним. Рівняння для струмів канонічного розрізу співпадають із загальновідомим формулюванням першого закону Кірхгофа, а більш загальною формою цих рівнянь є рівняння для струмів будь-якого розрізу, навіть неканонічного (в теоретичній електротехніці можна зустріти поняття узагальненого вузла, який, по суті, уособлює поняття розрізу).
Матриця Fт в другому рівнянні являє собою транспоновану топологічну матрицю. Щоб отримати транспоновану топологічну матрицю, необхідно стрічки топологічної матриці записати у вигляді стовпців.
6. Топологічні рівняння у скалярній форміДля отримання топологічних рівнянь у скалярній формі достатньо здійснити матричні операції множення. Ця операція здійснюється за правилом "стрічка на стовпець", згідно з яким треба обрати в лівій матриці стрічку, а в правій - стовпець, а далі кожний елемент стрічки помножити на відповідний елемент стовпця, а отримані добутки слід скласти. Одержаний результат дорівнює елементу матриці-результату, номер стрічки якого дорівнює номеру стрічки лівої матриці, а номер стовпця - номеру стовпця правої матриці.
Кількість рівнянь, отриманих від першого матричного рівняння, визначається кількістю зв’язків в орієнтованому графі системи, а кількість рівнянь від другого матричного рівняння ‑ кількістю віток у дереві орієнтованого графа системи. Таким чином, загальна кількість топологічних рівнянь дорівнює кількості ребер орграфа електричної системи. Однак ці рівняння не дають можливості отримати однозначні результати розв’язання, оскільки кількість невідомих змінних, що міститься навіть в цій системі, перевищує кількість рівнянь. Дійсно, для кожного резистора, конденсатора і котушки індуктивності маємо дві невідомі змінні, а для кожного джерела електричної енергії існує лише одна невідома змінна. Загальна кількість невідомих змінніх дорівнює подвійні кількості пасивних елементів (резисторів, конденсаторів, котушок індуктивностей), збільшена на кількість джерел енергії. Таким чином, для знаходження всіх невідомих змінних не вистачає рівнянь, кількість яких дорівнює кількості пасивних елементів. Ці рівняння можуть бути записані як так звані компонентні рівняння.
Математична модель №7
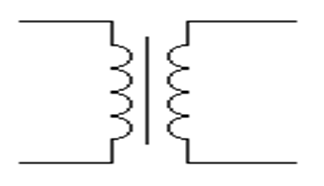
Скласти диференціальне рівняння трансформатора щодо напруги
U1 і U2 . Електричні параметри трансформатора наведені на малюнку де r1 , L1, i1 – опір, індуктивність і тік первинної обмотки; r1 , L1, i1 – те ж для вторинної обмотки; R – опір навантаження; U1 і U2 - вхідна напруги трансформатори; Ь – кофіцієнт взаємоіндукції обмоток.
Список літератури
1. Перхач В.С. Математичні задачі електроенергетики. Львів: Вища школа, 1989.- 464 с.
2. Электрические системы: Математические задачи электроэнергетики: Учебник /Под ред. В.А.Веникова.- М:, Высш. шк., 1981. -288 с.
3. Лудченко А.А., Лудченко Я.А., Примак Т.А.Основы научных исследований: Учеб. пособие / Под ред. А.А. Лудченко. — 2-е изд., стер. — К.: О-во "Знания", КОО, 2001. — 113 с.
4. http://psystat.at.ua/publ/3-1-0-13
5. Румшинский Л.З. Математическая обработка результатов эксперимента. — М.: Наука, 1971. — 192 с.
6. Сиденко В.М., Грушко ИМ. Основы научных исследований. — Харьков: Вища шк., 1979. — 200 с.
7. Чкалова О.Н. Основы научных исследований. — К.: Вища шк., 1978. — 120 с.
Похожие работы
... группы; 5) используется общее лабораторное оборудование и техника; 6) коллективная ответственность, т.е. за конечный итог отвечают все участники исследовательской работы. 3. Этапы теоретического исследования 3.1 Постановка проблемы Проблема (преграда, трудность - в переводе с древнегреческого) в научном познании является выражением несоответствия между достигнутым уровнем и объемом ...
... . Конкретные экономические дисциплины вырабатывают систему правил, необходимых для практической деятельности, а потому относятся не к области общей теории, а искусства в хозяйственной практике. Важнейшая задача теоретической экономики – быть “несущей конструкцией” не только всей системы экономических наук, но и учебных дисциплин, что является основой всей высшей экономической школы. Взаимосвязь ...
... социологического воображения и навыка его применения в социальной жизни является абсолютно необходимым в образовании социологов, как тех, кто планирует заниматься академической наукой, так и тех, кто выбирает профессии, ориентированные на практику. Социологическое воображение и теоретические ресурсы Развитие социологического воображения почти то же самое, что овладение социологической теорией ...
... , концепций, учений, в которых экономические и политические знания процессов обосновываются посредством соответствующих методов, законов, категорий и понятий. Прикладной уровень дисциплины «Исследование социально-экономических и политических процессов» – это анализ соответствующих частных методов практического решения тех или иных проблем, исходя из реальных практических целей и определенных ...



0 комментариев