Навигация
Расчетные схемы и способы расчета
3.2.2 Расчетные схемы и способы расчета
В расчетах используется гипотеза академика Н.Н.Павловского о независимости фильтрации в теле плотины и ее основании: Q = qтела + qосн.
При использовании гипотезы делается ряд допущений:
¾ рассматривается плоская схема фильтрации;
¾ водоупор принимается плоским, горизонтальным и абсолютно водонепроницаемым;
¾ грунт тела плотины и основания считается однородным и изотропным;
¾ слой воды в нижнем бьефе считается равным нулю;
¾ положение кривой депрессии не зависит от вида и фильтрационных свойств грунта тела плотины. Определяется оно положением уровней воды в бьефах и геометрическими размерами тела плотины.
Осуществляем выбор расчетной схемы. Для этого проводим ряд операций:
¾ разбиваем продольный профиль плотины на 3 части: одну русловую и две пойменные;
¾ в каждой из частей проводим сечение. Сечение I проводится в самой глубокой точки русловой части. В каждом сечении должен быть уровень воды в верхнем бьефе;
¾ составляем расчетную схему.
При расчете рассматриваем наполнение водохранилища до НПУ.
3.2.3 Депрессионная поверхность фильтрационного потока
Координаты кривой депрессии рассчитываются по формуле:
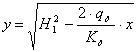 (18)
(18)
Для расчета координат депрессионной кривой необходимо иметь следующие исходные данные:
Сечение I-I
¾ высота плотины в сечении:
Нпл = ÑГП – ÑДна = 221,2–108,0 =13,2 м;
¾ глубина воды в верхнем бьефе:
Н1 = ÑНПУ – ÑДна = 218,1– 208,0 = 10,1 м;
d = Hпл – H1 = 13,2 – 10,1 = 3,1 м;
¾ горизонтальная проекция депрессионной кривой:
L = d∙m1 + B + Hпл∙m2 – Sдр = 3,1∙3 + 10 + 13,2∙2 – 7,18 = 38,52 м;
Lр = ∆l + L = 4,34 + 38,52 = 42,86 м,
где ∆l = β ∙ H1 = 0,43∙10,1 = 4,34 м,
где ![]() ;
;
¾ коэффициент фильтрации через тело плотины: Кф = 0,001 м/сут;
¾ координаты кривой депрессии, рассчитанные по формуле (18):
| x | 4,34 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 42,86 |
| y | 9,57 | 9,49 | 8,83 | 8,13 | 7,35 | 6,48 | 5,48 | 4,24 | 2,45 | 0 |
Сечение II-II
¾ высота плотины в сечении:
Нпл = ÑГП – ÑДна = 221,2 – 215,2 = 6 м;
¾ глубина воды в верхнем бьефе:
Н1 = ÑНПУ – ÑДна = 218,1– 215,2 = 2,9 м;
d = Hпл – H1 = 6 – 2,9 = 3,1 м;
¾ горизонтальная проекция депрессионной кривой:
L = d∙m1 + B + Hпл∙m2 – Sдр = 3,1∙3 + 10 + 6∙2 – 9,5 = 21,8 м;
Lр = ∆l + L = 1,25 + 21,8 = 23,05 м,
где ∆l = β ∙ H1 = 0,43∙2,9 = 1,25 м,
где ![]() ;
;
¾ коэффициент фильтрации через тело плотины: Кф = 0,001 м/сут.
¾ координаты кривой депрессии, рассчитанные по формуле (18):
| x | 1,25 | 5 | 10 | 15 | 20 | 21,8 |
| y | 2,85 | 2,57 | 2,19 | 1,74 | 1,10 | 0 |
Сечение III-III
¾ высота плотины в сечении:
Нпл = ÑГП – ÑДна = 221,2 – 216,9 = 4,3 м;
¾ глубина воды в верхнем бьефе:
Н1 = ÑНПУ – ÑДна = 218,1– 216,9 = 1,2 м;
d = Hпл – H1 = 4,3 – 1,2 = 3,1 м;
¾ горизонтальная проекция депрессионной кривой:
L = d∙m1 + B + Hпл∙m2 – Sдр = 3,1∙3 + 10 + 4,3∙2 – 9,5 = 18,4 м;
Lр = ∆l + L = 0,52 + 18,4 = 18,92 м,
где ∆l = β ∙ H1 = 0,43∙1,2 = 0,52 м,
где ![]() ;
;
¾ коэффициент фильтрации через тело плотины: Кф = 0,001 м/сут.
¾ координаты кривой депрессии, рассчитанные по формуле (18):
| x | 0,52 | 1 | 5 | 10 | 15 | 18,4 |
| y | 1,18 | 1,17 | 1,02 | 0,80 | 0,49 | 0 |
0 комментариев