Навигация
0 Sn10
_ 1
задавшись асортиментним вектором У2 = 0, отримаємо
:
0
0 S12
_ 1 S22 _
х = S: =: = S2
0 Sn2
Аналогічно, валовий випуск х, необхідний для виробництва одиниці кінцевого продукту к-й галузі, складе
0 S1k
_: S2k _
х = S 1 =: = Sk (9)
: Snk
0
тобто к-й стовпець матриці S.
З рівності (9) витікає наступне:
Щоб випустити тільки одиницю кінцевого продукту к-й галузі, необхідно в 1-ій галузі випустити х1=S1k, в 2-ій х2=S2k і так далі, в i-й галузі випустити xi=Sik і, нарешті, в n-й галузі випустити xn=Snk одиниць продукції.
Так при цьому виді кінцевого продукту виробництва тільки одиниця к-го продукту, то величини S1k, S2k., Sik., Snk, є коефіцієнти повних витрат продукції 1-й, 2-й і так далі, n-й галузей вказаної одиниці к-го продукту, що йде на виготовлення. Ми вже ввели раннє коефіцієнти прямих витрат a1k, a2k., aik., ank на одиницю продукції к-й галузі, які враховували лише ту частину продукції кожної галузі, яка споживається безпосередньо к-й галуззю. Але, очевидно, необхідно забезпечити замкнутий виробничий цикл. Якби продукція i-й галузі поступала б тільки в к-ю галузь в кількості aik, те виробництво к-й галузі все одно не було б забезпечено, бо було потрібно ще продукти 1-ої галузі (a1k), 2-ій галузі (a2k) і так далі А вони у свою чергу не зможуть працювати, якщо не отримуватимуть продукцію тієї ж i-й галузі (ai1, ai2. і так далі). Проілюструємо сказане на прикладі табл. 2
Хай нас не цікавить випуск для зовнішнього споживання продукції 2-ої галузі (k=2) і ми хочемо визначити витрати продукції 1-ої галузі на одиницю цієї продукції. З табл. 2 знаходимо, що на кожну одиницю продукції 2-ої галузі (х2=1) витрачається: продукції 1-ої галузі a12=0.4 і 2-ій галузі a22=0.1.
Такі будуть прямі витрати. Хай потрібно виготовити у2=100. Чи можна для цього планувати випуск 1-ої галузі х1=0.4100=40? Звичайно, не можна, оскільки необхідно враховувати, що 1-а галузь частина своєї продукції споживає сама (а11=0.2), і тому сумарний її випуск слід скоректувати: х1=40+0.240=48. Проте і ця цифра невірна, оскільки тепер уже слід виходити з нового об'єму продукції 1-ої галузі – х1=48 'і так далі Але справа не тільки в цьому. Згідно табл. 2 продукція 2-ої галузі також необхідна для виробництва і 1-ої і 2-ої галузей і тому потрібно буде випускати більше, ніж у2=100. Але тоді зростуть потреби в продукції 1-ої галузі. Тоді досить звернутися до складеної систем рівнянь, поклавши у1=0 і у2=1 (см п. 2):
0.8х1 – 0.4х2 = 0
-0.55х1 + 0.9х2 = 1
Вирішивши цю систему, отримаємо х1=0.8 і х2=1.5. Отже, для того, щоб виготовити одиницю кінцевого продукту 2-ої галузі, необхідно в 1-ій галузі випустити продукції х1=0.8. Цю величину називають коефіцієнтом повних витрат і позначають її через S12. Таким чином, якщо а12=0.4 характеризує витрати продукції 1-ої галузі на виробництво одиниці продукції 2-ої галузі, використовувані безпосередньо в 2-ій галузі (чому вони і були названі прямі витрати), то S12 враховують сукупні витрати продукції 1-ої галузі як прямі (а12), так і непрямі витрати, що реалізовуються через інші (в даному випадку через 1-у ж) галузі, але кінець кінцем необхідні для забезпечення випуску одиниці кінцевого продукту 2-ої галузі. Ці непрямі витрати складають S12-a12=0.8–0.4=0.4
Якщо коефіцієнт прямих витрат обчислюється на одиницю валового випуску, наприклад а12=0.4 при х2=1, то коефіцієнт повних витрат розраховується на одиницю кінцевого продукту.
Отже, величина Sik характеризує повні витрати продукції i-й галузі для виробництва одиниці кінцевого продукту к-й галузі, що включають як прямі (aik), так і непрямі (Sik – aik) витрати.
Очевидно, що завжди Sik > aik.
Якщо необхідно випустити уk одиниць к-го кінцевого продукту, то відповідний валовий випуск кожної галузі складе на підставі системи (8):
x1 = S1kyk·, x2 = S2kyk., xn = Snkyk
що можна записати коротше у вигляді:
x = Skyk· (10)
Нарешті, якщо потрібно випустити набір кінцевого продукту, заданий ассортиментным вектором У =:, то валовий випуск к-й галузі xk, необхідний для його забезпечення, визначиться на підставі рівності (10) як скалярний твір стовпця Sk на вектор У, тобто
xk = Sk1y1 + Sk2y2 +. + Sknyn = Sky (·11)·
а весь вектор-план х знайдеться з формули (7) як твір матриці S на вектор У.
Таким чином, підрахувавши матрицю повних витрат S, можна по формулах (7) – (11) розрахувати валовий випуск кожної галузі і сукупний валовий випуск всіх галузей при будь-якому заданому асортиментному векторі У.
Можна також визначити, яка зміна у вектор-плане Dх = (Dх1, Dх2., Dхn) викличе задану зміну асортиментного продукту У = (у1, у2., уn) по формулі:
Dх = SУ (·D12)
Приведемо приклад розрахунку коефіцієнтів повних витрат для балансової табл. 2. Ми маємо матрицю коефіцієнтів прямих витрат:
0.2 0.4
А =
0.55 0.1
Отже
1 -0.2 -0.4 0.8 -0.4
Е – А = =
-0.55 1 -0.1 -0.55 0.9
Визначник цієї матриці
0.8 -0.4
D [E – A] = = 0.5
-0.55 0.9
Побудуємо приєднану матрицю (Е – А)*. Маємо:
0.9 0.4
(Е – А)* =,
0.55 0.8
звідки зворотна матриця, що є таблицею коефіцієнтів повних витрат, буде наступною:
1 0.9 0.4 1.8 0.8
S = (Е – А)-1 = – =
0.5 0.55 0.8 1.1 1.6
З цієї матриці укладаємо, що повні витрати продукції 1-ої і 2-ої галузі, одиниці кінцевого продукту 1-ої галузі, що йдуть на виробництво, складає S11=0.8 і S21=1.5. Порівнюючи з прямими витратами а11=0.2 і а21=0.55, встановлюємо, непрямі витрати в цьому випадку складуть 1.8–0.2=1.6 і 1.1–0.55=0.55.
Аналогічно, повні витрати 1-ої і 2-ої галузі на виробництво одиниці кінцевого продукту 2-ої галузі рівні S12=0.8 і S22=1.5, звідки непрямі витрати складуть 0.8–0.4=0.4 і 1.6–0.1=1.5.
Хай потрібно виготовити 480 одиниць продукції 1-ою і 170 одиниць 2-ої галузей.
Тоді необхідний валовий випуск х = х1 знайдеться з рівності (7):
_ _ 1.8 0.8 480 1000
х = SУ = · =
1.1 1.6 170 800.
Повні витрати праці капіталовкладень
Розширимо табл. 1, включивши в неї, окрім продуктивних витрат xik, витрати праці, капіталовкладень і так далі по кожній галузі. Ці нові джерела витрат впишуться в таблицю як нові n+1-я, n+2-я і так далі додаткові рядки.
Позначимо витрати праці в к-ю галузь через xn+1, k, і витрати капіталовкладень – через xn+2, k (де до = 1, 2., n). Подібно до того як вводилися прямі витрати aik
xn+1, k
введемо в розгляд коефіцієнти прямих витрат праці an+1, k = –, і
xk
xn+2, k
капіталовкладень an+2, k = –, що є витратою відповідного
xk
ресурсу на одиницю продукції, що випускається к-й галуззю. Включивши ці коефіцієнти в структурну матрицю (тобто дописавши їх у вигляді додаткових рядків), отримаємо прямокутну матрицю коефіцієнтів прямих витрат.
При вирішення балансових рівнянь як і раніше використовується лише основна частина матриці (структурна матриця А). Проте при розрахунку на планований період витрат праці або капіталовкладень, необхідних для випуску даного кінцевого продукту, беруть участь додаткові рядки.
Так, хай, наприклад, проводиться одиниця продукту 1-ої галузі, тобто
_ 1
У = 0
:
0.
Для цього потрібний валовий випуск продукції
S11
_ _ S21
x = S1 =:
Sn1
Підрахуємо необхідні при цьому витрати праці Sn+1,1. Очевидно, виходячи з сенсу коефіцієнтів an+1, k прямих витрат праці як витрат на одиницю продукції к-й галузі і величин S11, S12., S1n, що характеризують скільки одиниць продукції необхідно випустити в кожній галузі, отримаємо витрати праці безпосередньо в 1-у галузь як an+1,1S11, в 2-у – an+1,2S21 і так далі, нарешті в n-ю галузь an+1, nSn1. Сумарні витрати праці, пов'язані з виробництвом одиниці кінцевого продукту 1-ої галузі, складуть:
Sn+1,1 = an+1,1S11 + an+1,2S21 +. + an+1, nSn1 = an+1S1
тобто рівні скалярному твору (n+1) – го рядка розширеної матриці А, 'яку позначимо an+1, на 1-й стовпець матриці S.
Сумарні витрати праці, необхідні для виробництва кінцевого продукту к-й галузі, складуть:
_ _
Sn+1, k = an+1Sk (13)
Назвемо ці величини коефіцієнтами повних витрат праці. Повторивши всі приведені міркування при розрахунку необхідних капіталовкладень, прийдемо аналогічно попередньому до коефіцієнтів повних витрат капіталовкладень:
Sn+2, k = an+2Sk (14)
Тепер можна доповнити матриць S рядками, що складаються з елементів Sn+1, k і Sn+2, k, утворити розширену матрицю коефіцієнтів повних витрат.
Користуючись цією матрицею можна розрахувати при будь-якому заданому асортиментному векторі У не тільки необхідний валовий випуск продукції х (для чого використовується матриця S), але і необхідні сумарні витрати праці xn+1, капіталовкладень xn+2 і так далі, що забезпечують випуск даної кінцевої продукції У.
Очевидно
xn+1 = Sn+1,1y1 + Sn+1,2y2 +. + Sn+1, nyn (16)
xn+2 = Sn+2,1y1 + Sn+2,2y2 +. + Sn+2, nyn
тобто сумарна кількість праці і капіталовкладень, необхідних для забезпечення асортиментного вектора кінцевої продукції У, рівні скалярним творам відповідних додаткових рядків матриці S 'вектор У.
Нарешті, об'єднуючи формулу (7) з формулами (16), приходимо до наступної компактної форми:
x1
x2
_: _
x = xn = SУ ('17)'
xn+1
xn+2
Хай додатково до даним, поміщеним в табл. 2, відомі за підсумками виконання балансу фактичні витрати праці xn+1, k (у тис. людино-годин) і капіталовкладень xn+2, k (у тис. крб.), які записані в табл. 3
Переходячи до коефіцієнтів прямих витрат aik, отримаємо розширену матрицю:
0.2 0.4
А' = 0.55 0.1
0.5 0.2
1.5 2.0
Зворотна матриця S = (E – A)-1 була вже підрахована в попередньому пункті.
На підставі (13) розрахуємо коефіцієнти повних витрат праці (Sn+1, k=S3, k):
S31 = a3S1· = 0.5 · 1.8 + 0.2 1.1 = 1.12;
S32 = a3S2· = 0.5 · 0.8 + 0.2 1.6 = 0.72
і капіталовкладень Sn+2, k = S4, k:
S41 = a4S1· = 1.5 · 1.8 + 2.0 1.1 = 4.9;
S42 = a4S2· = 1.5 · 0.8 + 2.0 1.6 = 4.4.
Таким чином, розширена матриця S 'коефіцієнтів повних витрат прийме вигляд:
1.8 0.8
S' = 1.1 1.6
1.12 0.72
4.9 4.4
Якщо задатися на планований період колишнім асортиментним вектором
У = 240, то розрахувавши по формулах (16) сумарні витрати праці xn+1 і 85 капіталовкладень xn+2, отримали б xn+1 = x3 = 1,12 · 240 + 0.72 · 85 = 268.8 + 61.2 = 330 тис. чіл.-ч. і xn+2 = xn = 4.9 240 + 4.4 85 = 1176 + 374 = 1550 тис. руб., що співпадає з початковими даними табл. 3.
Проте на відміну від табл. 3, де ці сумарні витрати групуються по галузях
(250 і 80 або 750 і 800), тут вони розподілені по видах кінцевої продукції: на продукцію 1-ої галузі 268.8 і на продукцію 2-ої галузі 61.2; відповідно витрати капіталовкладень складають 1176 і 374.
При будь-якому новому значенні асортиментного вектора У всі показники плану, такі, як валова продукція кожної галузі і сумарні витрати трудових ресурсів і капіталовкладень знайдемо з формули (17).
Так, хай заданий асортиментний вектор У = 480. Тоді
_ х1 1.8 0.8 1000
х = х2 = 1.1 1.6 480 = 800
х3 1.12 0.72 170 600
х4 4.9 4.4 3100
Звідси укладаємо, що запланований випуск кінцевого продукту У може бути досягнутий при валовому випуску 1-ої і 2-ої галузей: х1=1000 і х2=800, при сумарних витратах праці х3=660 тис. чіл.-ч. і при витратах капіталовкладень х4=3100 тыс. руб.
Розглянуті теоретичні питання і приклади розрахунку, звичайно, далеко не вичерпують важливу для практики область балансових досліджень. Тут проілюстрований тільки одне напрям додатку лінійної алгебри в економічних дослідженнях.
Завдання
У таблиці вказані витратні норми двох видів сировини і палива на одиницю продукції відповідного цеху, трудомісткість продукції в людино-годинах на одиницю продукції, вартість одиниці відповідного матеріалу і оплата за 1 чіл.-ч.
Визначити:
а) сумарна витрата сировини, палива і трудових ресурсів на виконання виробничої програми;
б) коефіцієнти прямих витрат сировини, палива і праці на одиницю кінцевої продукції кожного цеху;
в) витрата сировини, палива і трудових ресурсів по цехах;
г) виробничі витрати по цехах (у крб.) і на всю виробничу програму заводу;
д) виробничі витрати на одиницю кінцевої продукції.
Рішення:
а) Сумарна витрата сировини I можна отримати, помноживши відповідний 1-й рядок другої таблиці на вектор х, тобто
а4х = (1.4; 2.4; 0.8) 186 = 1088
Аналогічно можна отримати витрату сировини II і так далі
Все це зручно записати у вигляді твору:
1.4 2.4 0.8 235 1088 Сировина I
0 0.6 1.6 186 = 746 Сировина II
2.0 1.8 2.2 397 1678 Паливо
0.1 0.2 0.2 1409 Людино-годин.
б) Витрата сировини I на одиницю кінцевої продукції 1-го цеху (у1=1) знайдемо з виразу 1.4S11 + 2.4S21 + 0.8S31. Отже, відповідні коефіцієнти повних витрат сировини, палива і праці на кожну одиницю кінцевого продукту отримаємо з твору матриці:
I II III
1.4 2.4 0.8 1.04 0.21 0.02 1.97 2.92 1.36 Сировина I
0 0.6 1.6 0.21 1.05 0.13 = 0.17 0.84 2.09 Сировина II
2.0 1.8 2.2 0.03 0.13 1.26 2.53 2.60 5.23 Паливо
10 20 20 15.2 24.8 28.0 Праця
Таким чином, наприклад, для виготовлення у1=1 необхідно витратити 1.97 одиниць сировини I, 0.17 одиниць сировини II, 2.53 одиниць палива і 15.2 чіл.-ч.
в) Витрата сировини, палива і так далі по кожному з цехів отримаємо з множення їх витратних норм на відповідні валові випуски по цехах. В результаті отримаємо матрицю повних витрат:
I II III
Сировина I 330 440 318
Сировина II 0 111 635
Паливо 470 335 873
Праця 2350 3720 7940
г) Виробничі витрати по цехах можемо отримати шляхом множення зліва рядка вартостей (5; 12; 2; 1.2) на останню матрицю:
330 440 318
0 111 635 I II III
(5; 12; 2; 1.2) 470 335 873 = (5410; 8666; 20484)
2350 3720 7940
д) Нарешті, виробничі витрати на одиницю кінцевої продукції, необхідні для визначення собівартості продукції, можемо знайти шляхом множення зліва матриці повних витрат, знайденої в п.б., на рядок цін:
1.97 2.92 1.36
0.17 0.84 2.09 I II III
(5; 12; 2; 1.2) 2.53 2.60 5.23 = (35.3; 59.6; 75.7)
15.2 24.8 28.0
Таким чином, внутрішньовиробничі витрати на одиницю товарної продукції I, II і III цехів відповідно складають: 35.3 крб., 59.6 крб., 75.7 крб.
Похожие работы
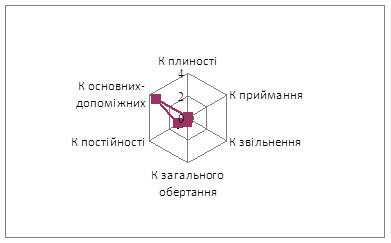
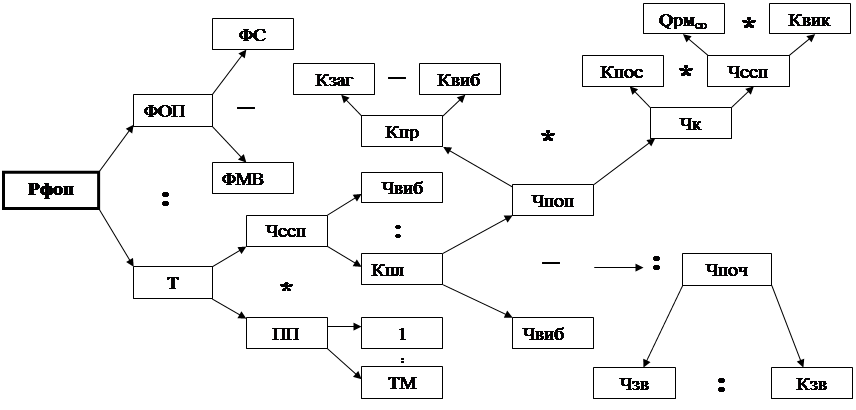
... ефективно , і, хоча, має великий потенціал, показники які виступають передумовою подальшого розвитку потенціалу підприємства не на належному рівні. По-четверте було проведено аналіз впливу факторів на підвищення ефективності використання трудового потенціалу підприємства, для цього було обрано два показника – рівень фонду оплати праці та продуктивність праці. Аналіз показав , що на збільшення рі ...
... тільки не значимою масою і річною програмою випуску визначаємо за формулою Nпр = Тшт.к 60/ + tшт.к Де Тшт.к – трудомісткість річного приведеного випуску деталей T шт. к – трудоємкість виготовлення деталі в хв. Nпр = 91000 60/29.77 = 183406.11 шт Приймаємо Nпр = 183406 шт Кількість верстатів вхідних в нормативну зону обслуговування визначаємо по формулі Но = ( Тмв/Тз + 1 )Кдз ...

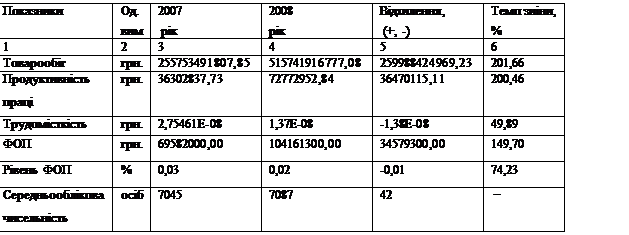

0 комментариев