Математическая модель и решение задачи оптимального управления

2. Математическая модель и решение задачи оптимального управления

 

Результатом статистического анализа показателей, характеризующих экономический процесс, являются оценки функций регрессии случайных величин (показателей) на одну величину или систему случайных величин. Совокупность всех этих зависимостей является математическим описанием системы и законов перехода ее из одного состояния в другое. Принцип оптимального управления состоит в выборе таких значений показателей, при которых система начинает функционировать наилучшим образом.

Прежде всего, необходимо выбрать критерий оптимальности, т.е. функцию, значение которой должно достичь наибольшего (или наименьшего) из всех возможных в данной ситуации значений. С точки зрения статистического анализа это – один из результативных признаков. Управляемые переменные этой задачи оптимизации – факторные признаки, оказывающие воздействие на результативный признак. Факторные признаки также связаны между собой. Эта связь описывается оценкой функции регрессии одного из факторных признаков на другой факторный признак, полученной в результате регрессионного анализа статистических данных. Выбор таких связанных пар факторных признаков начинается с корреляционного анализа, где отправной точкой является достаточно большой коэффициент парной корреляции. При выборе управляемых переменных задачи следует учесть, что из тесно связанных факторных признаков, особенно с коэффициентом парной корреляции большем 0.5, только один воздействует на результативный признак самостоятельно, а воздействие другого является опосредствованным. Поэтому при выборе математической модели критерия оптимальности учитывается только один из них, а воздействие другого заложено в оценке функции его регрессии на первый фактор.

Оценки функций регрессии факторных признаков (управляемых переменных) друг на друга накладывают ограничения на их возможные значения. Но это не единственные ограничения. Необходимо учесть, что каждый из факторных признаков может принимать значения только в строго ограниченных пределах, которые вытекают из сути самого показателя.

В общем случае математическая модель задачи оптимального управления экономическим процессом, составленная в результате многомерного статистического анализа показателей, содержит:

– целевую функцию

y = f (x₁,x₂,…,x_k) –

функцию регрессии результативного признака Y на факторные признаки X₁,X₂,…,X_k ;

– ограничения, определяющие область допустимых решений :

x_j = φ_i (x_i) , ( i, j = 1,2,…,k) –

функции регрессии факторного признака X_j на факторный признак X_i (i≠J);

 , ( i = 1,2,…,k),

где  и  – нижняя и верхняя границы значений X_i .

Задача оптимизации формулируется следующим образом:

Найти такие значения управляемых переменных, удовлетворяющие всем ограничениям задачи, при которых целевая функция достигает искомого экстремального значения.

В общем случае задача является задачей нелинейного программирования, так как хотя бы одна из функций f (x₁,x₂,…,x_k) или φ_i (x_i) (i = 1,2,…,k) нелинейна относительно управляемых переменных.

Для рассмотренного примера математическая модель имеет вид:

 

Y2 =247,9641 – 930,3571*X4 + 73,538*X8 + 1009,39*X4^2 –

–4,44689*X8^2 – 140,1884*X4*X8 ––> max

X5 = 2,4605*X7^3 – 10,061*X7^2+13,815*X7–5,6226

X6 = 18,481*X4^3– 15,579*X4^2+2,8223*X4+0,3562

X8 = -86,539*X7^4+518,28*X7^3-1141,3*X7^2+1098,8*X7-390,07

0,2<=X4<=0,5 0,6<=X5<=0,9

0 <=X6<=0,7 1 <=X7<= 2 0 <=X8<= 4

Для решения задачи нелинейной оптимизации следует воспользоваться надстройкой Excel Поиск решения. Алгоритм необходимых действий для приведенной математической модели :

1.  На рабочем листе Excel расположить исходные данные (см.рис.14).

2.  В ячейки A1–E1 записать имена управляемых переменных, в ячейку G1 – имя целевой функции.

3.  В ячейки A2 и E2 ввести значения 1, как значения переменных, вошедших в целевую функцию ( при решении нелинейных задач не рекомендуется задавать начальные нулевые значения), значения остальных переменных можно оставлять нулевыми .После окончания поиска решения в ячейках A1–E1 появятся оптимальные значения управляемых переменных, а в ячейке G2 –оптимальное значение целевой функции.

	A	B	C	D	E	F	G	H
1	X4	X5	X6	X7	X8		Y2
2	0,2	0,722559	0,445348	1,2115	1,161317	Искомые	149,1756	ЦФ
3	0,2	0,6	0	1	0	Нижняя гр.
4	0,5	0,9	0,7	2	4	Верхняя гр.
5		0,722559	0,445348		1,161316	Зависимости
6		X5=F(X7)	X6=F(X4)		X8=F(X7)
7

Рис.14.Данные для Поиска решения.

 

4.  В ячейки A3–E3 ввести нижние допустимые значения управляемых переменных , в ячейки A4-E4 – верхние.

5.  В ячейки B5, C5 , E5 ввести формулы зависимостей, накладывающих ограничения на значения управляемых переменных, в соответствии с математической моделью и адресами (№ ячеек) переменных (рис.15).

6.  В ячейку G2 ввести формулу зависимости целевой функции от управляемых переменных (рис.15).

	A	B	C	D
1	X4	X5	X6	X7
2	0,2	0,722575104348201	0,445348	1,21149967733427
3	0,2	0,6	0	1
4	0,5	0,9	0,7	2
5		=2,4605*D2^3-10,061*D2^2+13,815*D2-5,6226	=18,481*A2^3-15,579*A2^2+2,8223*A2+0,3562

	E
1	X8
2	1,16131678195123
3	0
4	4
5	=-86,539*D2^4+518,28*D2^3-1141,3*D2^2+1098,8*D2-390,07

	G
1	Y2
2	=247,9641-930,036*A2+73,538*E2+1009,39*A2^2-4,44689*E2^2-140,*A2*E2

7.  Вызвать Сервис – Поиск решения .

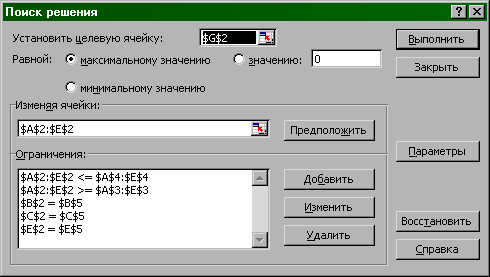
Рис.16. Компьютерная модель задачи.

8.  В диалоговом окне ввести необходимые данные (см. рис.16). Для ввода Ограничений щелкнуть по кнопке Добавить и в появившемся диалоговом окне ввести необходимые ссылки и знаки неравенств, как указано на рис.16.

9. Выполнить.

10. Проанализировать полученные результаты и выработать рекомендации по обеспечению оптимального управления.

Как видно из рис.14, оптимальное решение при данных ограничениях и зависимостях свелось к таким результатам.

Максимальное значение индекса снижения себестоимости продукции (Y2 = 149,1756 ) достигается при таких значениях признаков:

трудоемкость единицы продукции X4 = 0,5 ;

удельный вес рабочих в составе ППП X5 = 0,7226 ;

удельный вес покупных изделий X6 = 0,4453 ;

коэффициент сменности оборудования X7 = 1,2114 ;

премии и вознаграждения на одного работника X8 = 1,1613 .

Литература

 

1.  Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 1997. – 248 с.

2.  Дубров А.М. , Мхитарян В.С. , Трошин Л.И. Многомерные статистические методы : Учебник. – М.: Финансы и статистика, 2000. – 352 с.

3.  Колемаев В.А. и др. Теория вероятностей и математическая статистика: Учеб. пособие для экон. спец. вузов / В.А.Колемаев, О.В.Староверов, В.Б.Турундаевский ; Под ред. В.А.Колемаева . – М.: Высш. шк. , !991. – 400 с.

4.  Исследование операций в экономике : Учебн. пособие для вузов / Н.Ш.Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман ; Под ред. Н.Ш.Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 407 с.

5.  Сивец С.А. Статистические методы в оценке недвижимости и бизнесе. Учебно-практическое пособие по статистике для оценщиков. – Запорожье, 2001. – 320 с.

6.  Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере / Под ред. Фигурнова В.Э. – М.: ИНФРА , 1998. – 528 с.

7.  Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. – М.: Высш. шк. , 1986. – 319 с.

8.  Савицкая Г.В. Анализ хозяйственной деятельности предприятия. – Минск: ООО «Новое знание», 2000. – 668 с.

9.  Ларсен, Рональд У. Инженерные расчеты в Excel.: Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 544 с.

10.  Гурман В.Е. Теория вероятностей и математическая статистика. Учеб. Пособие для втузов. М., « Высш. школа», 1977. – 479 с.

11.  Математическая статистика: Учебник / Иванова В.М., Калинина В.Н., Нешумова Л.А. и др. – М.: Высш. школа, 1981. –371 с.

12.  Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV – Санки-Петербург, 1997. – 384 с.

Приложение

 

Показатели производственно-хозяйственной деятельности предприятий

 

В таблице приведены следующие показатели производственно-хозяйственной деятельности предприятий

- производительность труда (среднегодовая выработка продукции на одного работника), тыс. грн.;

 - индекс снижения себестоимости продукции;

Y₃ - рентабельность, %;

X₄ - трудоемкость единицы продукции;

- удельный вес рабочих в составе промышленно-

 производственного персонала (ППП);

- удельный вес покупных изделий;

- коэффициент сменности оборудования;

- премии и вознаграждения на одного работника, %;

- удельный вес потерь от брака, %;

- фондоотдача, грн;

- среднегодовая численность ППП, чел.;

- среднегодовая стоимость основных производственных фондов (ОПФ), тыс. грн.;

- среднегодовой фонд заработной платы ППП, тыс. грн.;

- фондовооруженность труда, грн.;

- оборачиваемость нормируемых оборотных средств, дни;

- оборачиваемость ненормируемых оборотных средств, дни;

- непроизводственные расходы, %.