Переход к обычной энергетической шкале с использованием подста-новок (3.74б и 3.74в) дает

3.5.9. Переход к обычной энергетической шкале с использованием подста-новок (3.74б и 3.74в) дает

 . (3.92)

Согласно формуле (3.92), уровни гармонического осциллятора эквидис-тантны, и интервал между.ними равен .

 

3.5.10. Продолжая исследование лесенки уровней, учтем, что сверху она неограничена, но нижняя граница определена уровнем основного состояния Ψ₀, ниже которого не существует состояний системы. Поэтому попытка подействовать оператором понижения  на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора:

(3.93)

Здесь целесообразно вернуться к переменной х. С учетом выражения для (3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для :

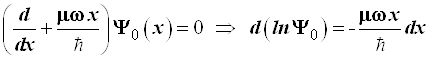, (3.94)

при интегрировании которого получим волновую функцию основного состояния:

. (3.95)

Далее находим нормировочный множитель А₀:

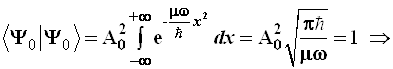 (3.96)

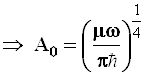.  (3.97)

При раскрытии выражения (3.96) использован интеграл Пуассона:

.

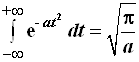3.5.11. Волновая функция  является собственной функцией гамильто-ниана. Поэтому для расчета основного уровня достаточно подействовать по-следним на и определить собственное значение

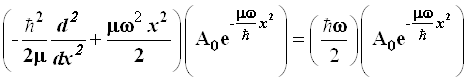(3.98)

Энергия искомого основного уровня равна 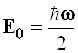. (3.99)

Последовательными сдвигами на  вверх, согласно уравнению (3.92), получается вся лесенка энергетических уровней, и схема квантования энергии осциллятора передается формулой:

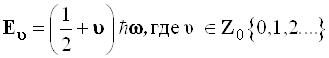(3.100)

 

3.5.12. Оператор повышения  позволяет получить весь спектр волновых функций из . Если υ раз подействовать оператором  на , то получится с точностью до постоянного множителя. Иными словами, генератор волновой функции υ-го состояния – это оператор повышения, возведенный в степень υ:

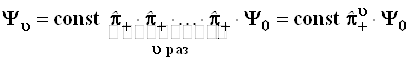 . (3.101)

Напомним, что любое преобразование волновой функции, в общем случае, порождает необходимость новой нормировки.

3.5.13. Обсудим вид волновых функций осциллятора. Для этого удобно произвести еще одно упрощение за счет замены переменной путем подстановки:

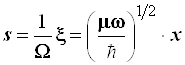,  (3.102)

благодаря чему  и оператор повышения , необходимый для полу-чения , примут вид:

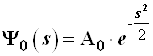,  (3.103)

. (3.104)

Постоянный коэффициент в выражении (3.104) ие играет роли, так как к функции Ψ_υ , генерируемой по формуле (3.105), он добавляет лишь множитель , который далее автоматически входит в состав нормировочного множителя А_υ, и поэтому Ψ_υ передается формулой:

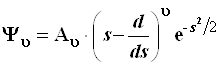 (3.105)

Оператор 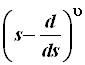 представляет собой бином, составленный из степеней переменной s и оператора дифференцирования , который в свою очередь извлекает из гауссовой экспоненты  степенные множители, в результате выражение (3.105) преобразуется к виду:

 , (3.106)

где  – многочлен степени υ, называемый полиномом Эрмита. Нетрудно убедиться, что эти полиномы можно представить выражением, которое легко запоминается, благодаря своей симметричности:

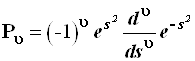.  (3.107)

Последовательно придавая υ значения 0, 1, 2, 3 …, читатель легко может вывести формулы полиномов Эрмита разных порядков. Для того, чтобы читатель смог проверить свои расчеты, приведем в табл.2 несколько первых полиномов Эрмита вместе с их корнями и графиками. В табл.2 также изображены графики ненормированных волновых функций

 =.

 У волновых функций имеется один и тот же множитель – экспонента ; эта быстро спадающая к нулю функция при удалении от начала координат “прижимает” к оси абсцисс расходящиеся было ветви полиномов. В результате получается картина, очень напоминающая поведение волновых функции “ящика”.

Табл.2.

Полиномы Эрмита и волновые функции гармонияеского

осциллятора

υ		Корни полиномов	Графики полиномов	Графики волновых функций .
0	1	-
1	2s	0
2	4s2 - 2	±1/√2
3	8s3 - 12 s	0; ±3/2
4	16s4-48s2+12	±0,525; ±1,651

Читатель может сам получить формулу для нормировочных коэффициентов или взять их готовое выражение:

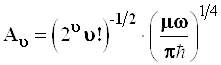. (3.108)

 

3.5.14. Прямыми вычислениями нетрудно еще раз проверить свойство ортогональности волновых функций. Интегрирование по всей области возможных значений переменной х дает:

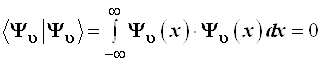,  (3.109)

что наглядно видно из графиков табл. 2

Напомним, что свойство ортогональности – это общее свойство собствен-ных функций любого эрмитова оператора, к числу которых относится и гамильтониан.

 

3.5.15. Все полиномы Эрмита и порождаемые ими волновые функции делятся на два класса – четные и нечетные. Ранее подобное свойство наблюдалось у волновых функций “ящика” и “ротатора”. Анализ четности волновых функций и их произведений оказывается очень полезным при оценке различных характеристик системы. Рассмотрим это на примерах.

Покажем, что среднее отклонение колеблющейся системы от положения равновесия равно нулю. Следуя 5-му постулату, запишем для υ=0:

. (3.110)

Подинтегральное выражение нечетное, так как образовано в виде произве-дения по правилу (чет × нечет × чет). Интеграл, взятый в симметричных пределах от нечетной функций, тождественно равен нулю, так что . Это же имеет место и для других состояний.

3.5.16. Иначе обстоит дело со среднеквадратичным отклонением , на-зываемым среднеквадратичной амплитудой осциллятора. Произведем соответ-ствующие расчеты; вновь обращаясь к 5-му постулату:

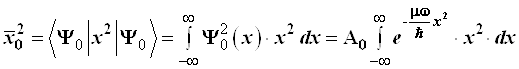, (3.111)

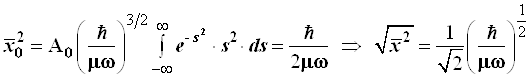 (3.112)

В преобразовании (3.112) использован табличный интеграл

.  (3.113)

 

3.5.17. Сравним среднеквадратичное отклонение  с квадратом ампли-туды, предсказываемой на основе формулы, связывающей классическое и квантово-механическое выражение для полной энергии:

,  (3.114)

откуда 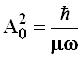  и 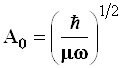 . (3.115)

Формулы (3.112) и (3.115) практически дают один и тот же результат, поскольку классическая амплитуда А₀ – это максимальное отклонение осциллятора от положения равновесия, тогда как квадратичная “амплитуда” усреднена по всем положениям осциллятора, а понятие точной траектории и предельного отклонения не имеет смысла в квантовой механике.

Можно показать, что соответствие классической амплитуды и квантово-механического среднеквадратичного отклонения сохраняется и в других состояниях осциллятора, а именно:

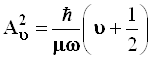и 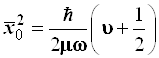(3.120)

 (в квазиклассическом подходе) (в квантовомеханическом подходе)

 

3.5.18. Среднеквадратичные амплитуды играют важную роль в экспериментах, связанных с определением равновесных положений ядер в молекулах, например, в электронографии или в рентгеноструктурном анализе. Они также позволяют на основе опытных колебательных спектров (инфракрасного поглощения и комбинационного рассеяния) определить пределы изменения молекулярных “размеров” за счет колебательных деформаций ядерного остова молекулы.

  3.6. Сравнение свойств “ящика”, “ротатора” и осциллятора.

3.6.1. Три рассмотренные модели простейших одномерных движений в ограниченном пространстве позволяют проследить некоторые общие качественные закономерности, касающиеся состояний и уровней квантово-механических систем. Они наглядно проявляются при сопоставлении энергетических диаграмм и графиков волновых функций “частицы в ящике”, “гармонического осциллятора” и “плоского ротатора”.

 

3.6.2. В первом случае потенциальная энергия нулевая на выделенном интервале, и, как говорят, потенциальная “яма” имеет прямоугольную форму. Во втором случае потенциальная энергия изменяется квадратично при отклонении от равновесия и говорят о параболической форме потенциальной “ямы”. Наконец, ротатор отсутствием потенциальной энергии напоминает “ящик”. Отсюда, хотя способы нумераций уровней и отличаются, схемы квантования энергии у этих систем одинаковы – уровни расходятся с возрастанием квантового числа.

У гармонического осциллятора квантование энергии уникально – уровни эквидистантны. Благодаря этому при взаимодействии с квантами света частота поглощаемого излучения совпадает с собственной частотой молекулярного осциллятора, например, колеблющихся атомов, связанных химической связью.

Таким образом, квантование полной энергии системы определяется потенциальной функцией.

3.6.3. В разделе 3.2.5. мы связали вырождение уровней ротатора с равноправием двух направлений вращения вокруг оси. Можно высказать еще и более общее утверждение, связывающее наличие вырождения с порядком вращательной оси системы. Плоский ротатор – это система с осью вращения бесконечного порядка. Далее будет показано, что вырожденные уровни появляются у систем, имеющих ось третьего порядка и выше.

В целом же, нам удалось приобрести некоторые необходимые навыки в решении простейших задач квантовой механики.