Обчислюється надлишковий попит, який дорівнює

4. Обчислюється надлишковий попит, який дорівнює

Якщо  з точністю до  дорівнює 0, тоді процес обчислення цін припиняється та вважається, що сформовано рівноважну систему цін, яка задовольняє і фірму й споживача.

5. Якщо  з точністю до  не дорівнює 0, то аукціонником за наступними формулами здійснюється регуляція цін

, ,

,

де  й  – додатні коефіцієнти корекції.

3. Задача визначення рівноважного випуску продукції

Складемо алгоритм, який визначає на основі міжгалузевого аналізу величину випуску за допомогою моделі Леонтьєва при відомій матриці коефіцієнтів прямих витрат  і векторів кінцевого попиту .

Для розв’язання даної задачі використовуємо обчислювальну схему Гаусса-Зейделя.

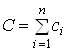Визначимо перелік змінних: – кількість секторів економіки;  – матриця коефіцієнтів прямих витрат;  – кінцевий попит на -й продукт; – ітераційний розв’язок -го порядку; – значення критерію збіжності;  – загальна сума абсолютних відхилень;  – лічильник ітерацій; – загальний кінцевий попит;  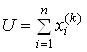– загальний випуск.

Під час використання методу Гаусса-Зейделя як основні рівняння виступають такі:

,

,

………………………………………

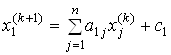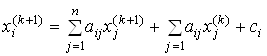, (7)

………………………………………

,

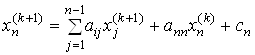Де ,  

Якщо розбити матрицю коефіцієнтів прямих витрат по діагоналях на дві частини: ,

Де

,

,

то систему (7) можна записати у вигляді

.

Зауважимо, що – кількість секторів економіки,  – коефіцієнти матриці коефіцієнтів прямих витрат,  – коефіцієнти вектора кінцевого попиту. Вважається, що

.

Ітераційний процес триває доти, доки

.

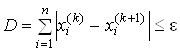4. Оптимізаційні задачі в моделі Леонтьєва

 

Сформулюємо наступну екстремальну задачу. Нехай вектор трудових ресурсів дорівнює , де  – витрати трудових ресурсів -ї галузі. Суму 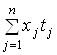 назвемо обсягом витрат ресурсів, необхідних для виробництва валового продукту . Позначимо через  загальний об’єм трудових ресурсів, . Тоді має місце нерівність 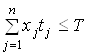. Розв’язок системи рівнянь  при 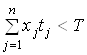 існує, але не при будь-якому невід’ємному векторі . Нехай вектор  задає не кінцевий попит, а лише структуру кінцевого попиту, тобто можна вважати, що . Необхідно максимізувати  – кіль-кість комплектів товарів, що випускають, тобто

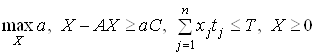. (8)

Суть задачі (3.13) полягає в раціональному розподілі трудових ресурсів під час виробництва номенклатури товарів.

Якщо матриця  продуктивна, то задача (8) припустима й має розв’язок. Справді, якщо , то існує додатне  таке, що

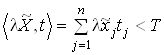
Значення  є припустимим для задачі (8). Очевидно, що множина всіх припустимих значень є обмеженою, отже, задача (8) має розв’язок.

Розглянемо узагальнену модель Леонтьева (УМЛ), в якій передбачається, що кожна галузь має не один технологічний спосіб для виробництва свого продукту. Нехай у виробничій системі є  типів товарів і  технологічних процесів , кожен з яких випускає один товар.

Позначимо кількість ресурсу -го типу й об'єму роботи, необхідних для виробництва одиниці продукції виду  в галузі  за допомогою технології , відповідно як

 

 

тоді узагальнену матрицю коефіцієнтів прямих витрат (узагальнену матрицю Леонтьєва) і вектор коефіцієнтів трудових витрат можна визначити як

.

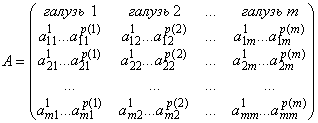
Матриця коефіцієнтів випуску виходить із одиничної матриці шляхом такого розширення:

.

Виразимо вектор обсягу випуску, що описує режим роботи всіх технологічних способів узагальненої моделі Леонтьєва, як

.

Вектор кінцевого попиту

.

Кожна галузь вибирає з кількості доступних їй технологій одну певну технологію. Якщо припустити, що вибір технологій здійснюється з урахуванням задоволення кінцевого попиту , який пропонують кожній з галузей, так, щоб мінімізувати об'єм витрат „живої" роботи в суспільстві в цілому, то задача технологічного вибору може бути наведена у вигляді задачі лінійного програмування

. (9)

Для сформульованої узагальненої моделі Леонтьєва існує так називана теорія заміщення: якщо в УМЛ припустити можливість виробництва додатного вектора попиту , то, як би не змінювався кінцевий попит, оптимальний базис  залишатиметься незмінним. Цей базис є матрицею розміру . Оскільки будь-яка галузь має виробляти певну кількість продукції, причому це можливо за допомогою різних виробничих технологій, кожною галуззю буде обраний один технологічний процес.

В моделі (9) в явному вигляді присутній лише один з обмежених ресурсів – робота. Однак більш реалістично вважати, що рівень діяльності обмежений не тільки роботою, але в залежності від вибору тривалості періоду виробництва також й основними фондами, головними складеними елементами яких є виробничі будинки й верстати, а також землею й багатьма іншими ресурсами. Обмеження ресурсів можна виразити у вигляді системи нерівностей. Якщо позначити обсяг ресурсу , необхідний для випуску в галузі , як  де  а обсяг ресурсу , що насправді є в наявності, як  де тоді реально досяжний обсяг випуску має відповідати такій умові:

,

де ,

.

Якщо ввести умови обмеженості ресурсів в задачу (9), то можна записати її в більш загальному вигляді:

 (10)

Вектор обмежень ресурсів можна вважати невід’ємним, тому очевидно, що задача (10) аналогічна задачі лінійного програмування. Якщо вважати задачу (10) вихідною й навести її у вигляді

 (11)

то двоїста їй задача записується так:

 (12)

де  – вектор цін на продукцію,  – вектор цін на ресурси.

Розв’язок задачі (12), тобто оптимальна система цін , збігається з симплексним мультиплікатором, який відповідає оптимальному базису задачі (11). Через те, що константи системи обмежень ресурсів не додатні, елементи симплексного мультиплікатора для ресурсів є невід’ємними. Якщо матрицю діяльності, що утворює оптимальний базис, і відповідний їй вектор коефіцієнтів трудових витрат навести як

то синтез оптимальних цін можна записати так:

або інакше

. (13)

Формула (3.18) означає, що ціна продукції дорівнює сумі витрат продуктів виробництва, обмежених ресурсів і роботи. Всі витрати виражаються у вартісному вигляді. Якщо як обмежений ресурс розглядати тільки роботу, то (13) прийме такий вигляд:

. (14)

Симплексний критерій

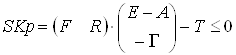 (15)

інтерпретують як критерій прибутковості технологічного процесу . Співвідношення (15) означає, що технологія, яка не відповідає критерію прибутковості, – це застаріла технологія й її вибрано не буде. Крім того, симплексний критерій для задачі (13) означає, що ресурс , який існує в кількості, що перевищує оптимально використовуваний об’єм, став ресурсом свободним, а його ціна перетворюється на нуль.