Навигация
Анализ и прогнозирование экономических показателей на основе регрессионных моделей
5. Анализ и прогнозирование экономических показателей на основе регрессионных моделей
Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.
Прогнозируемое значение переменной ![]() получается при подстановке в уравнение регрессии
получается при подстановке в уравнение регрессии
![]() (5.1)
(5.1)
ожидаемой величины фактора ![]() . Данный прогноз называется точечным. Значение независимой переменной
. Данный прогноз называется точечным. Значение независимой переменной ![]() не должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.
не должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.
Вероятность реализации точечного прогноза теоретически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.
доверительные интервалы, зависят от стандартной ошибки , удаления ![]() от своего среднего значения
от своего среднего значения ![]() , количества наблюдений n и уровня значимости прогноза α. В частности, для прогноза будущие значения
, количества наблюдений n и уровня значимости прогноза α. В частности, для прогноза будущие значения ![]() с вероятностью (1 - α) попадут в интервал
с вероятностью (1 - α) попадут в интервал
![]()
![]()
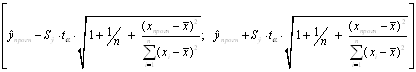 .
.
6. Измерение связей неколичественных переменных
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.
Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.
Оценить тесноту связи между признаками можно с помощью коэффициентов взаимной сопряженности и коэффициентов контингенции или ассоциации.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.
При ранжировании каждой единице совокупности присваивается ранг, т. е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (р) и Кендэлла (X). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
Сущность метода Спирмена (Spearman) состоит в следующем:
1) располагают варианты факторного признака по возрастанию — ранжируют единицы по значению признака X;
2) для каждой единицы совокупности указывают ранг с точки зрения результативного признака У.
Если связь между признаками прямая, то с увеличением ранга признака X ранг признака У также будет возрастать; при тесной связи ранги признаков X и У в основном совпадут. При обратной связи возрастанию рангов признака X будет, как правило, соответствовать убывание рангов признака У. В случае отсутствия связи последовательность рангов признака У не будет обнаруживать никакого порядка возрастания или убывания.
Теснота связи между признаками оценивается ранговым коэффициентом корреляции Спирмена ( в случае, когда нет связанных рангов):
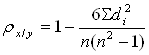
![]() - квадрат разности рангов;
- квадрат разности рангов;
n – число наблюдений ( число пар рангов).
Коэффициент корреляции Спирмена принимает значение в интервале (-1,+1). Чем ближе он к единице, тем более тесня связь между признаками. Знак коэффициента показывает направление связи.
Литература
1. Гусаров В.М., «Теория статистики», – М.: Аудит, ЮНИТИ, 2002;
2. Громыко Г.Л. Теория статистики: учеб. – М., Изд-во Инфра-М, 2000.
3. Ефимова М.П., Петрова Е.В., Румянцев В.Н., «Общая теория статистики», - М.: “Инфра - М”, 2003;
4. «Практикум по статистике: Учеб. пособие для вузов» / Под ред. В. М. Симчеры / ВЗФЭИ. – М.: ЗАО «Финстатинформ», 2000; Симчера В.М. Практикум по статистике: учеб. пособ. – М. Изд-во Финстатинформ, 1999.
5. Шмойлва Р.А. Практикум по теории статистики: учеб. пособ. – М., Изд-во Финансы и статистика, 2002.
Похожие работы
... тот специфический для данной науки круг вопросов, которые подлежат исследованию при изучении наукой своего объекта познания. Принципы, методы и приемы изучения предмета науки образуют методологию этой науки. Объектом изучения социально-экономической статистики является общество во всем многообразии его форм и проявлений. Это связывает социально-экономическую статистику со всеми другими науками, ...
... усиливает актуальность этого вопроса. 5. Преодоление существующей несопоставимости показателей социальной статистики и показателей, представленных в других отраслевых статистиках. 6. Моделирование социально-экономических связей с целью обнаружения механизмов взаимодействия в общественной системе. На макроуровне представлен ряд объективно существующих ограничительных факторов, ...
... уравнения для оценки неизвестных значении зависимой переменной. Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей. Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается ...
... агрегатный индекс производительности труда – Уt= . Наиболее типичным общим индексом количественных показателей является индекс физического объема, который записывается в виде формулы: Уq= . В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие показатели качественных характеристик, как средняя цена, средняя себестоимость, средняя производительность труда и другие. ...

0 комментариев