Саратовский государственный технический университет
Кафедра «Системотехника»
Расчетно-графическая работа
по математической логике
на тему: «Моделирование машины Тьюринга»
Выполнил:
студент группы АСУ-21
Мустафин Ш. Р.
Проверил:
преподаватель
Минаев С.В.
Саратов 2010
Цель
Изучение принципов работы машины Тьюринга, приобретение практических навыков программирования машины Тьюринга.
Задание
Изучить правила написания алгоритмов на эмуляторе машины Тьюринга;
Получить у преподавателя вариант задания для реализации алгоритма;
Разработать алгоритм в соответствии с полученным заданием;
Отладить написанный алгоритм на эмуляторе машины Тьюринга.
Задача
Сложение нескольких чисел в двоичной системе.
Описание метода решения
Для более удобной реализации алгоритма на эмуляторе, сложение будет выполняться поэтапно. Сначала будем складывать два первых слагаемых, затем результат этого сложения с третьим и так далее, пока не дойдем до знака «=». Первым шагом ищется самый младший, неиспользованный разряд первого слагаемого. В зависимости от его значения переходим в следующие соответствующие состояния. Далее ищем самый младший, неиспользованный разряд второго слагаемого и записываем на его место результат сложения этих двух разрядов. Затем снова возвращаемся на первый шаг. Этот цикл осуществляется до тех пор, пока у одного из слагаемых не кончатся разряды. Записываем оставшиеся старшие разряды к результату, с учетом переноса, если он есть. Стираем лишние символы, находящиеся до старших разрядов результата. Проверяем какой знак стоит после результата. Если «+», то возвращаемся к первому шагу, если «=», то конец подсчетам.
Описание программы
Для удобства в программе все 1 и 0 заменяются на I и O соотвественно. Далее состояние q5 доходит до + и переходит в состояние q6, в зависимости от того, какой символ стоит перед + q6 переходит в q16 – i, q15 – o. q16, q7, q9 – это состояния которые несут единицу во второе слагаемое без переноса, и в зависимости от значения, записывают в самый младший, неиспользованный разряд результат сложения. Если переноса нет, то переходим в состояние q11, есть – q10. Q11,q13 – бегут к первому слагаемому и анализируют самый младший, неиспользованный разряд и в зависимости от значения переходят в состояния q16 и q15, если разрядов нету, то в q14. Q14 и q17 затирают ненужные символы и переходят в состояние q6. Q15, q37,q39 - это состояния которые несут ноль во второе слагаемое без переноса, и в зависимости от значения, записывают в самый младший, неиспользованный разряд результат сложения и переходят в состояние q11. Q10,q23 – бегут с переносом к первому слагаемому и анализируют самый младший, неиспользованный разряд и в зависимости от значения переходят в состояния q16 и q26, если разрядов нету, то в q24. Q26 аналог q15, только несет значение 0 с переносом. Q24 аналог q14, но с учетом переноса. Программа останавливается, когда одно из состояний, преобразую частичную сумму, после младшего разряда находит символ «=».
Алгоритм решения
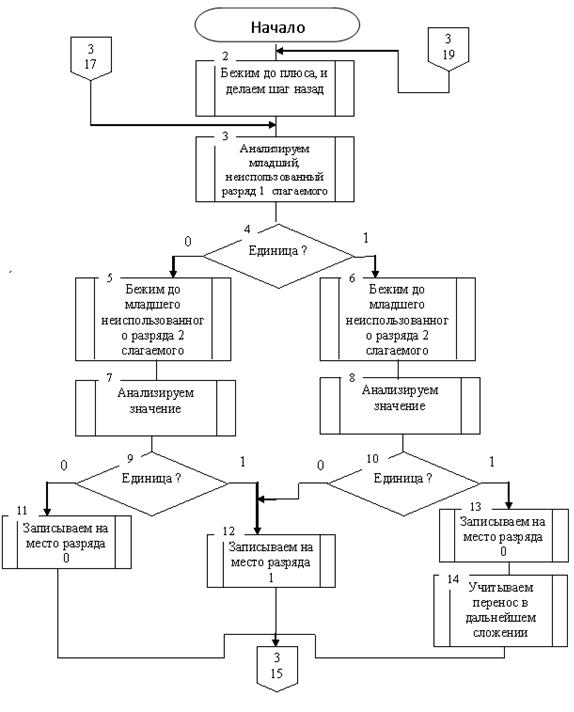
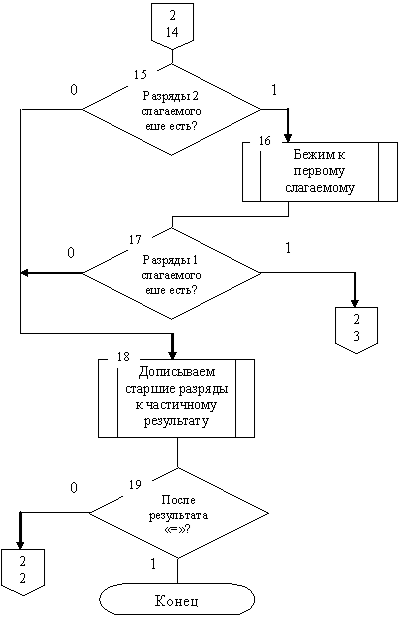
Код программы
[MoT Data]
1110111+111111+10101010101010101010+…++11=
q1s q1s dR
q1s1q1sidR
q1s0q1sodR
q1s+q1s+dR
q1s=q2s=dL
q2siq2sidL
q2soq2sodL
q2s+q2s+dL
q2s q5s dR
q5s q5s dR
q5siq5sidR
q5soq5sodR
q5s+q6s+dL
q5s=q100s=dE
q6siq16s*dR (если цифра первого слагаемого 1 без переноса)
q6soq15s*dR ( если цифра первого слагаемого 0 без переноса)
q16s+q16s+dR
q16s*q16s*dR
q16siq7sidR
q16soq7sodR(проход по звездочкам и + до еденичек или и и о)
q16s1q40s1dL
q16s0q40s0dL
q40s+q12s1dL(q12 когда разряды кончились во втором слагаемом)
q7siq7sidR
q7soq7sodR
q7s+q9s+dL(q7 и q9 - несу 1 без переноса )
q7s1q9s1dL
q7s0q9s0dL
q7s=q9s=dL
q9siq10s0dL (q10 - c переносом единичкой)
q9soq11s1dL (q11 без переноса )
q9s+q12s1dE (q12 когда разряды кончились во втором слагаемом без переноса)
q11siq11sidL
q11soq11sodL(бежит назад без переноса )
q11s+q11s+dL
q11s*q13s*dL
q13s*q13s*dL
q13siq16s*dR
q13soq15s*dR
q13s q14s dR( q14 если разряды закончились в первом слагаемом без переноса )
q14s q14s dR
q14s*q14s dR (восстановления числа в i и o )
q14s+q14s dR
q14siq14sidR
q14soq14sodR
q14s1q17s1dE
q14s0q17s0dE
q17s1q17sidR
q17s0q17sodR(вернуться в q6 после воосстановления)
q17s+q6s+dL
q17s=q100s=dE
q12s*q12s*dL(записать число без переноса )
q12s q21s dR
q12siq18s*dR
q12soq19s*dR
q18s*q18s*dR(нести единицу к цифрам через + и *)
q18s+q18s+dR
q18s1q20s1dL
q18s0q20s0dL
q20s+q12s1dL
q20s*q12s1dL
q19s*q19s*dR
q19s+q19s+dR (нести 0)
q19s1q22s1dL
q19s0q22s0dL
q22s+q12s0dL
q22s*q12s0dL
q21s q21s dR
q21s*q21s dR (q21 - шагает вправо стирает * и делает 1 и 0 - i и o до + или =)
q21siq21sidR
q21soq21sodR
q21s1q21sidR
q21s0q21sodR
q21s+q6s+dL
q21s=q100s=dE
q10siq10sidL (бежит назад с переносом )
q10soq10sodL
q10s+q10s+dL
q10s*q23s*dL
q23s*q23s*dL (бежит назад c переносом )
q23siq26s*dR
q23soq16s*dE
q23s q24s dR
q26s+q26s+dR проход по звездочкам и + до еденичек или и и о)
q26s*q26s*dR
q26siq25sidR
q26soq25sodR
q26s1q43s1dL
q26s0q43s0dL
q43s+q27s0dL
q25siq25sidR (q25 несу с переносом )
q25soq25sodR
q25s+q28s+dL
q25s1q28s1dL
q25s0q28s0dL
q25s=q28s=dL
q28siq10s1dL(q10 - c переносом единичкой)
q28soq10s0dL
q28s+q27s0dL
q24s*q24s dR
q24s+q24s dR ( q24 если разряды закончились в первом слагаемом с переносом)
q24siq24sidR
q24soq24sodR (восстановления числа в i и o )
q24s1q29s1dL
q24s0q29s0dL
q29siq29s0dL
q29soq30sodE
q29s q30s dE
q30soq17s1dE
q30s q17s1dE
q27s*q27s*dL (q27? когда разряды кончились во втором слагаемом с переносом)
q27s q31s dR
q27siq32s*dR
q27soq33s*dR
q32s*q32s*dR(нести единицу к цифрам через + и *)
q32s+q32s+dR
q32s1q34s1dL
q32s0q34s0dL
q34s+q27s0dL
q34s*q27s0dL
q33s*q33s*dR (нести 0)
q33s+q33s+dR
q33s1q35s1dL
q33s0q35s0dL
q35s+q12s1dL
q35s*q12s1dL
q31s*q31s*dR(q31 - шагает вправо стирает * и делает 1 и 0 - i и o до + или = надо дорисовать 1)
q31s0q36s0dL
q31s1q36s1dL
q36s*q21s1dL
q15s+q15s+dR
q15s*q15s*dR
q15siq37sidR
q15soq37sodR
q15s1q42s1dL
q15s0q42s0dL
q42s+q12s0dL
q37s*q37s*dR
q37siq37sidR
q37soq37sodR
q37s+q39s+dL
q37s1q39s1dL
q37s0q39s0dL
q37s=q39s=dL
q39siq11s1dL
q39soq11s0dL
q39s+q12s0dL
q100s=q100s=dL
q100siq100s1dL
q100soq100s0dL
q100s qz
Вывод
Входе выполнения задания были изучены принципы работы машины Тьюринга, приобретены практические навыки программирования машины Тьюринга.
Похожие работы
... обучения, yi и yj –выходные сигналы i-го и j-го нейронов. В настоящее время существует множество разнообразных обучающих правил (алгоритмов обучения). Глава IV Может ли компьютер мыслить? 4.1 Реально ли компьютерное мышление? Наконец я подошел к заключительной главе своей работы. В предыдущих главах была изложена сущность построения систем искусственного интеллекта, было рассказано о ...
... компьютационным состояниям автомата. Однако, условием возможности соответствий последнего рода является (по мнению Блока и Фодора) исчисляемость психологических состояний организма. 3. «Машинное» решение проблемы языка мысли Как возможен частный язык мысли? Если допустить, что аргумент от бесконечного регресса, опирающийся на положение, что все языки, которыми мы владеем, приобретены нами ...
... смысле, когда имеется в виду не только понимание в диалоге, но и понимание, осознание целей и результатов интеллектуальной деятельности. Отсюда следует и практическая трудность в моделировании творческих процессов (эвристической деятельности и психических функций), заключающаяся в необходимости отыскания и формализации тех элементов творческого процесса, которые свободно и неосознанно ...
... более сложных систем с целью познания происходящих в них процессов - воспроизводства жизни, обучения и так далее. Наиболее известно техническое значение кибернетики - создание на основе кибернетических принципов ЭВМ, роботов, ПЭВМ, породившее тенденцию кибернетизации и информатизации не только научного познания, но и ...

0 комментариев