Команда: fsolve ( )

3. Команда: fsolve ( )

По умолчанию Maple пытается найти аналитическое выражение для корней уравнения. Если это не удается, то, как отмечалось выше, в области вывода ничего не печатается. В подобных случаях (если корни действительно существуют) можно воспользоваться командой fsolve(), которая находит численное решение уравнения или системы уравнений. Формат команды отличается от формата команды solve() наличием третьего параметра опция:

fsolve (уравнения, переменные, опция);

Задание первых двух параметров соответствует заданию аналогичных параметров в команде solve(), а параметр опция может принимать значения из таблицы 1.

Таблица 1. Значения параметра опцuя команды fsolve ( )

Значение	Смысл
complex	Разыскиваются комплексные корни (только для полиномов)
Fulldigits	Используется арифметика с максимальной мантиссой
Maxsols=n	Разыскивается n решений (только для полиномов)
а.. b или x=a..b	Задан промежуток [а, b], на котором разыскивается решение (во второй форме задания этой опции х обозначает имя неизвестной переменной в уравнении)

Для произвольного уравнения по умолчанию эта функция находит одно решение, но для полиномов определяются все действительные корни. Для нахождения всех корней полинома, включая комплексные, следует задать опцию complex. В примере 4 показано использование команды численного решения уравнений.

Пример 4. Численное решение уравнений.

> eq:=x^4+2*x^2-2=0;

> s:=fsolve(eq,x);

> s:=fsolve(eq,x,complex);

> fsolve(ln(sin(x))=0,x);

> fsolve(ln(sin(x))=0,x,x=2..infinity);

> fsolve(ln(sin(x))=0,x,x=15..infinity);

Здесь также показано, как можно последовательно находить корни произвольного уравнения, задавая интервал изменения неизвестной величины с учетом полученного решения на предыдущем шаге нахождения корня (последние три команды).

4. Другие команды решения уравнений

Кроме универсальных команд solve () и fsolve () решения уравнений и систем уравнений, система Maple содержит специализированные команды, предназначенные либо для решения определенного класса уравнений, либо нахождения решений в заданном числовом поле. Здесь эти команды описаны предельно кратко для того, чтобы читатель знал об их существовании. Более подробно об этих командах можно узнать в справочной системе Maple, выполнив команду ?имя_команды, где вместо параметра имя_команды следует подставить ее действительное имя.

Команда isolve () ищет все целые решения уравнений. Если в уравнении задано несколько неизвестных, то строится решение относительно всех заданных неизвестных.

Пример 5. Целочисленное решение уравнений.

> isolve({(x+1)*(x-1/2)*(x-2)=0});

> isolve({5*x+6*y=1});

В решении последнего уравнения примера 5 использована целочисленная переменная _Z1 сгенерированная Maple.

Команда msolve () также ищет целочисленные решения уравнения, но только по модулю, заданному вторым параметром.

Пример 6. Целочисленное решение уравнений по заданному целому модулю.

> solve({3*x-4*y=1,7*x+y=2});

> msolve({3*x-4*y=1,7*x+y=2},11);

> msolve({3^n=4},11);

Команда rsolve () строит общее решение рекуррентного уравнения, используя начальные значения, если они заданы, или через их символьные обозначения, если они не заданы.

Пример 7. Решение рекуррентных уравнений.

> rsolve({F(n+2)=F(n+1)+F(n)},F(n)); # Без начальных условий

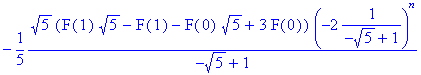
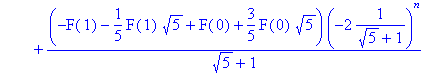
> rsolve({F(n+2)=F(n+1)+F(n),F(0)=1,F(1)=1},{F(n)});

 # Используя заданные начальные условия

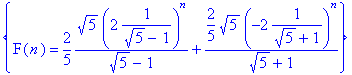
5. Решение неравенств

Команда solve () используется для решения неравенств и систем неравенств в области вещественных чисел точно так же, как и для решения уравнений и систем уравнений. Ответ выражается либо в виде множества неравенств, либо через функции RealRange () и Open (). Первая определяет замкнутый отрезок действительных чисел, а вторая используется для указания того, что граничная точка не входит в построенное решение. Для задания решения в виде множества, следует задать в виде множества либо само неравенство, либо неизвестную, относительно которой ищется решение. Если этого не сделать, то ответ будет получен с использованием указанных функций определения действительных отрезков.

Пример 8. Решение неравенств.

> solve((x+3)/(4-x)>4,x);

> solve((x+3)/(4-x)>4,{x});

> solve(log[1/2](log[2](x^2-8))>=-1);

> solve({log[1/2](log[2](x^2-8))>=-1});

В примере 8 решены два неравенства, для каждого из которых построено решение в виде множества и в форме действительных интервалов.

Литература

1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. – М.: Мир, 1997. – 208 с.

2. Дьяконов В.П. Математическая система Maple V. – М.: Издательство “Солон”,1998.

3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.

4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.:БХВ - Петербург, 2001.– 528 с.

5. Манзон Б.М. Maple V Power Edition – М.: Информационно-издательский дом “Филинъ”,1998г.