Схемы шифрования AES, RC4, RC5, RC6, Twofish, Mars

Федеральное агентство по образованию

Пензенский Государственный Университет

Кафедра «Информационная безопасность систем и технологий»

Реферат

на тему: «Схемы шифрования AES, RC4, RC5, RC6, Twofish, Mars»

Дисциплина: КМЗИ

Группа:

Выполнил:Принял:

Пенза 2006

Содержание

1. Алгоритм шифрования AES

2. Алгоритм шифрования MARS

3. Алгоритм шифрования RC4

4. Алгоритм шифрования RC5

5. Алгоритм шифрования RC6

6. Алгоритм шифрования Twofish

Список использованных источников

1. Алгоритм шифрования AES

Алгоритм DES (Data Encryption Standard), разработанный корпорацией IBM и являвшийся с 1977 федеральным стандартом шифрования данных США, использовался для шифрования не только правительством США, но и получил широкое распространение по всему миру среди частных пользователей. С ростом вычислительной мощности компьютеров стали возникать вопросы о криптостойкости DES'a перед вскрытием методом "грубой силы", но стандарт успешно проходил повторные сертификации, проводившиеся в 1983, 1988 и 1993. Хотя к середине 90х годов стало очевидным несоответствие общепринятого стандарта шифрования DES (Data Encryption Standard) современным требованиям. В первую очередь из-за недостаточной длины ключа всего в 56 бит. По данным Брюса Шнайера уже в 1993 году существовали устройства способные вскрыть DES за приемлемое время.

Процесс разработки нового федерального информационного стандарта (FIPS) для шифрования данных Advanced Encryption Standard (AES) был инициирован Национальным Институтом стандартов и технологий (NIST).

В начале января 1997 года NIST объявил о начале разработки AES, выпустив документ "Announcing development of a federal information processing standard for advanced encryption standard", содержащий первичные требования к алгоритму. [2]

Алгоритм шифрования AES должен быть открыто опубликован.

Алгоритм должен быть симметричным блочным шифром.

AES должен предусматривать возможность увеличения длины ключа.

AES должен быть легко реализуем и аппаратной и программно.

AES должен распространяться бесплатно или быть общедоступным в рамках патентов ANSI.

В сентябре 1997 года вышел уточняющий документ "Call for AES Candidate Algorithms", объявлявший о проведении конкурса на AES и содержащий официальные требования к кандидатам. В частности алгоритм должен поддерживать следующие комбинации длин блока и ключа 128-128, 128-192 и 128-256 битов. К 15 июню 1998 году был заявлен 21 криптографический алгоритм, но только 15 из которых удовлетворяли первоначальным требованиям. [3]

Страна происхождения	Алгоритм	Авторы
Australia	LOKI97	Lawrie Brown, Josef Pieprzyk, Jennifer Seberry
Belgium	RIJNDAEL	Joan Daemen, Vincent Rijmen
Canada	CAST-256	Entrust Technologies, Inc
	DEAL	Richard Outerbridge, Lars Knudsen
Costa Rica	FROG	TecApro Internacional S.A.
France	DFC	Centre National pour la Recherche Scientifique
Germany	MAGENTA	Deutsche Telekom AG
Japan	E2	Nippon Telegraph and Telephone Corporation
Korea	CRYPTON	Future Systems, Inc
USA	HPC	Rich Schroeppel
	MARS	IBM
	RC6	RSA Laboratories
	SAFER+	Cylink Corporation
	TWOFISH	Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall, Niels Ferguson
UK, Israel, Norway	SERPENT	Ross Anderson, Eli Biham, Lars Knudsen

В конце августа 1998 года в Калифорнии состоялась конференция, посвященная отбору кандидатов на AES, получившая название AES1. На конференции давались краткие описания алгоритмов шифрования, и были даны ответы на накопленные вопросы.

В качестве основных критериев оценки алгоритмов были [3]:

- Криптостойкость. Проводилось сравнение алгоритмов на степень независимости выходного блока от случайной перестановки битов входного блока, подверженность известным криптоатакам. Каждый кандидат должен был представить оценочную криптостойкость алгоритма.

-Стоимость. Кандидат предоставлял информацию о лицензионных соглашениях и патентах на алгоритм. Также учитывалась производительность алгоритма (скорость шифрования), необходимый для шифрования размер памяти.

-Особенности алгоритма и его реализации. Гибкость, аппаратное и программное удобство реализации.

В апреле 1999 года в Риме состоялась конференция AES2, в рамках которой проводились сравнение производительности программных реализаций алгоритмов с оптимизациями под языки С и Java. Наибольшую скорость шифрования/дешифрования показал алгоритм Crypton (40 Мбайт/с), наименьшую Magenta и НРС (2Мбайт/с). Хотя при проведении тестов на разных платформах и с различными компиляторами, полученные результаты довольно сильно различались. Все блочные алгоритмы можно разбить на две основные группы:

использующие сети Фейстеля

сети перестановок-подстановок (SP-сети) основанные на последовательных перестановках и подстановках, зависящих от ключа.

Среди алгоритмов-претендентов к первым относятся CAST-256, DEAL, DFC, E2, LOKI97, MAGENTA, MARS, RC6, TWOFISH, ко вторым CRYPTON, Rijndael, SAFER+ и SERPENT. Алгоритмы FROG и НРС не подпадали ни под одну из категорий, но входе обсуждения кандидатов не выявлено каких-либо выдающихся качеств данных алгоритмов.

В результате первичного обсуждения была выявлена слабая криптостойкость алгоритма MAGENTA, вскоре появились данные по криптоанализу алгоритмов FROG, LOKI, показывающие слабости алгоритмов относительно других алгоритмов. Также часть алгоритмов имели низкие шансы на успех из-за крайне малой скорости шифрования/дешифрования.

Отбор финалистов по названным критериям продолжался до начала августа 1999г.

9августа NIST выпустила пресс-релиз "Announces AES Finalists", в котором объявлялось о пяти финалистах: MARS, RC6, Rijndael, Serpent, TwoFish.

Rijndael

Формат блоков данных и число раундов

RIJNDAEL - это симметричный блочный шифр, оперирующий блоками данных размером 128 и длиной ключа 128, 192 или 256 бит - название стандарта соответственно "AES-128", "AES-192", и "AES-256".

Введем следующие обозначения:

Nb — число 32-битных слов содержащихся во входном блоке, Nb - 4;

Nk - число 32-битных слов содержащихся в ключе шифрования, Nk = 4,6,8;

Nr - число раундов шифрования, как функция от Nb и Nk, Nr = 10,12,14.

Входные (input), промежуточные (state) и выходные (output) результаты преобразований, выполняемых в рамках криптоалгоритма, называются состояниями (State). Состояние можно представить в виде матрицы 4 х Nb, элементами которой являются байты (четыре строки по Nb байт) в порядке S00,S10,S20,S30,Sm,Sn,S21,S31,---. Рисунок 1.1 демонстрирует такое представление, носящее название архитектуры «Квадрат».

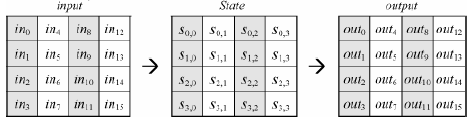
Рисунок 1.1 «Пример представления блока в виде матрицы 4xNb».

На старте процессов шифрования и дешифрования массив входных данных то, щ, ..., щ 5 преобразуется в массив State по правилу s[r,c] = in[r + 4c], где 0<г<4 и 0 < с < Nb. В конце действия алгоритма выполняется обратное преобразование out[r + 4c] = s[r,c], где 0<г<4 и 0<c<Nb - выходные данные получаются из байтов состояния в том же порядке.

Четыре байта в каждом столбце состояния представляют собой 32-битное слово, если г - номер строки в состоянии, то одновременно он является индексом каждого байта в этом слове. Следовательно состояние можно представить как одномерный массив 32-битных слов wo,...,wN , где номер столбца состояния с есть индекс в этом массиве. Тогда состояние можно представить так:

Ключ шифрования также как и массив State представляется в виде прямоугольного массива с четырьмя строками. Число столбцов этого массива равно Nk.

Для алгоритма AES число раундов Nr определяется на старте в зависимости от значения Ж (Таблица 1.1):

	Nk	Nb	Nr
AES-128	4	4	10
AES-192	6	4	12
AES - 256	8	4	14

Таблица 1.1 «Зависимость значения Nr от Nk и Nb »

Функция зашифрования

Введем следующие обозначения:

SubBytes() - замена байтов- побайтовая нелинейная подстановка в State-блоках (S-Вох) с использованием фиксированной таблицы замен размерностью 8x256 (affain map table);

ShiftRows() - сдвиг строк - циклический сдвиг строк массива State на различное количество байт;

MixColumns() - перемешивание столбцов - умножение столбцов состояния, рассматриваемых как многочлены над GF(28);

AddRoundKey() - сложение с раундовым ключом - поразрядное XOR содержимого State с текущим фрагментом развернутого ключа.

На псевдокоде операция зашифрования выглядит следующим образом:

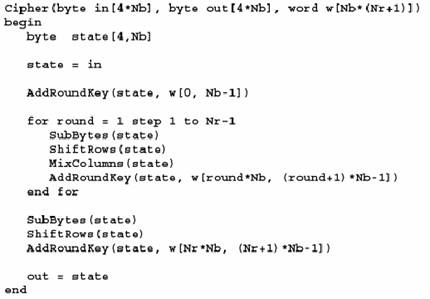
Рисунок 1.2 «Операция зашифрования, реализованная на псевдокоде»

После заполнения массива State элементами входных данных к нему применяется преобразование AddRoundKeyQ, далее, в зависимости от величины Nk, массив State подвергается трансформации раундовой 10, 12 или 14 раз, причем в финальный раунд является несколько укороченным - в нем отсутствует преобразование MixColumnsQ. Выходными данными описанной последовательности операций является шифротекст - результат действия функции зашифрования AES.

Функции расшифрования

В спецификации алгоритма AES предлагаются два вида реализаций функции расшифрования отличающихся друг от друга последовательностью приложения преобразований обратных преобразованиям функции зашифрования и последовательностью планирования ключей (см. ниже).

Введем следующие обозначения:

InvSubBytes() — обратная SubBytes() замена байтов- побайтовая нелинейная подстановка в SWe-блоках с использованием фиксированной таблицы замен размерностью 8x256 (inverse affain map);

InvShiftRows() — обратный сдвиг строк ShiftRows()— циклический сдвиг строк массива State на различное количество байт;

InvMixColumns() - восстановление значений столбцов - умножение столбцов состояния, рассматриваемых как многочлены над GF(28);

Функция обратного расшифрования

Если вместо SubBytes{), ShiftRows{ ), MixColumns{) и AddRoundKey{) в обратной последовательности выполнить инверсные им преобразования, можно построить функцию обратного расшифрования. При этом порядок использования раундовых ключей является обратным по отношению к тому, который используется при зашифровании. На псевдокоде она выглядит так:

Рисунок 1.3 «Операция обратного расшифрования реализованная на псевдокоде»

Функция прямого расшифрования

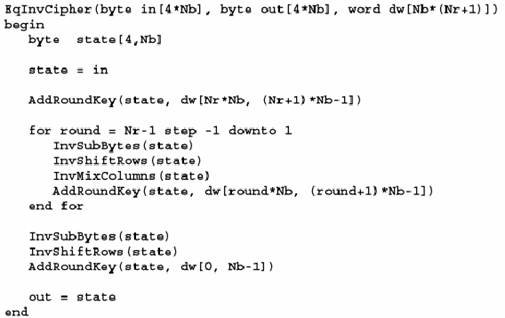
Рисунок 1.4 «Операция прямого расшифрования реализованная на псевдокоде»

Алгоритм обратного расшифрования, описанный выше имеет порядок приложения операций-функций обратный порядку операций в алгоритме прямого зашифрования, но использует те же параметры развёрнутого ключа. Изменив определенным образом после- довательность планирования ключа можно построить еще один алгоритм - алгоритм прямого расшифрования (Рисунок 3.4).

Два следующих свойства позволяют сделать это:

Порядок приложения функций SubBytes() и ShiftRows() не играет роли. То же са мое верно и для операций InvSubBytes() и InvShiftRows(). Это происходит потому, что функции SubBytes() и InvSubBytes() работают с байтами , а операции ShiftRows() и InvShiftRows() сдвигают целые байты, не затрагивая их значений.

Операция MixColumns() является линейной относительно входных данных, что означает InvMixColumns(State XOR RoundKey) = = InvMixColumns(State) XOR InvMixColumns(RoundKey)

Эти свойства функций алгоритма шифрования позволяют изменить порядок применения функций InvSubBytes() и InvShiftRows(). Функции AddRounKey() и InvMixCol-umns() также могут быть применены в обратном порядке, но при условии, что столбцы (32-битные слова) развёрнутого ключа расшифрования предварительно пропущены через функцию InvMixColumns().

Таким образом, можно реализовать более эффективный способ расшифрования с тем же порядком приложения функций как и в алгоритме зашифрования.

Алгоритм выработки ключей (Key Schedule)

Введем следующие обозначения: Rconf] - массив 32-битных раундовых констант;

RotWord() — операция циклической перестановки входного 4-байтного слова в выходное по следующему правилу [а0, ai, а2, а3 ] —> [ах, а2, а3, а0 ];

SubWord() - операция замены в 4-байтном слове с помощью S-Box каждого байта;

Å - операция исключающего или XOR.

Рисунок 1.5 «Операция планирования (расширения) ключа реализованная на псевдокоде»

Раундовые ключи получаются из ключа шифрования посредством алгоритма выработки ключей. Он содержит два компонента: расширение ключа (Key Expansion) и выбор раундового ключа (Round Key Selection). Основополагающие принципы алгоритма выглядят следующим образом:

общее число битов раундовых ключей равно длине блока, умноженной на число раундов, плюс 1;

ключ шифрования расширяется в расширенный ключ (Expanded Key);

раундовые ключи берутся из расширенного ключа следующим образом: первый раундовый ключ содержит первые Nb слов, второй - следующие Nb слов и т. д.

Расширение (планирование) ключа

Расширенный ключ (Рисунок 3.6) представляет собой линейный массив w[i] состоящий из A(Nr +1) 4-байтовых слов, i = О,4(Nr +1).

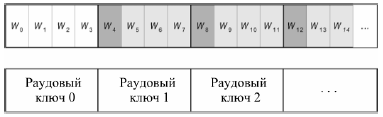
Рисунок 1.6 «Процедуры расширения и выборки раундового ключа для Nk = 4».

Светло-серым цветом выделены слова расширенного ключа, которые формируются без использования функций SubWord() и RotWord().

Темно-серым цветом ,выделены слова расширенного ключа, при вычислении которых используются преобразования SubWord() и RotWord())»

Первые Nk слов содержат ключ шифрования. Каждое последующее слово w[i] получается посредством XOR предыдущего слова w[i-1] и слова на Nk позиций ранее:

w[i- Nk]: w[i]= w[i-1] Å w[i- Nk].

Для слов, позиция которых кратна Nk, перед XOR применяется преобразование к w[i-1], а затем еще прибавляется раундовая константа Rcon[i] . Преобразование реализуется с помощью двух дополнительных функций: RotWord() и SubWord().

Значение Rcon[j] равно 2j-1 . Значение w[i] в этом случае определяется выражением: w[i] = SubWord(RotWord(w[i-1]) Å Rcon[i/Nk] Å M[i-Nk].

Выбор раундового ключа i-тый раундовый ключ выбирается из слов массива расширенного ключа в промежутке от W[Nb * i] до W[Nb * (i+1)].

Для функции зашифрования расширенный ключ генерируется алгоритмом Рисунок 1.5. Для функции обратного расшифрования используется этот же ключ, но в обратной последовательности начиная с последнего раундового подключа зашифрования.

Для функции прямого расшифрования используется несколько модифицированный алгоритм планирования ключа. При формировании развёрнутого ключа в процедуру планирования необходимо добавить в конце дополнительное преобразование (Рисунок 3.7), причем расширенный ключ используется при прямом расшифровании в той же последовательности, что и при зашифровании.

Рисунок 1.7 «Дополнительное преобразование расширенного ключа для функции прямого расшифрования»

Раундовое преобразование

Раундовое преобразование состоит из последовательного применения к массиву State ряда трансформаций.. Сейчас обсудим детали его реализации.

Нелинейная замена байтов массива состояния посредством трансформации SubBytesQ имеет вид:

Многократное вычисление в процессе зашифрования данного выражения оказывало бы неоправданную вычислительную нагрузку на исполняющую систему, поэтому для практической реализации наиболее приемлемым решением является использование предварительно вычисленной таблицы замены S-Box. Логика работы S-Box при преобразовании байта {ху} отражена в шестнадцатеричном виде на Рисунке 1.8:

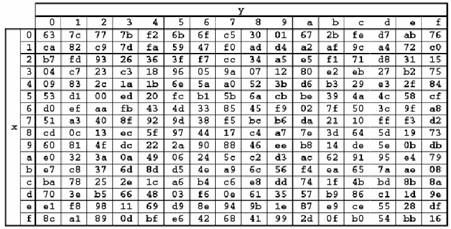
Рисунок 1.8 «Таблица S-Box замены байт»

Ее использование сводит операцию SubBytesQ к простейшей выборке байта из массива λ(f) = Sbox[f].

В функциях расшифрования применяется операция обратная InvSub-Bytes().

Она реализуется так же просто, как и предыдущая посредством инверсной таблицы S-Box – λ-1(f) = InvSbox[f]., ее логика работы при преобразовании байта {ху} отражена в шестнадцатеричном виде на Рисунке 1.9

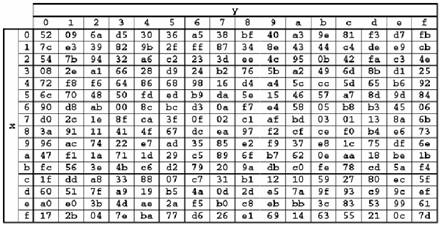
Рисунок 1.9 «Таблица S-Box инверсной замены байт»

Рисунок 1.10 иллюстрирует применение преобразования замены байт к состоянию в функциях зашифрования и расшифрования:

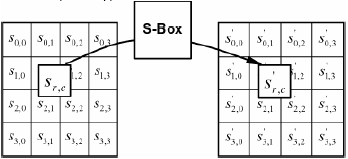
Рисунок 1.10 «Преобразование состояния посредством таблицы замены S-Box»

В преобразовании сдвига строк (ShiftRows) последние 3 строки состояния циклически сдвигаются ВЛЕВО на различное число байтов. Строка 1 сдвигается на С1 байт, строка 2 - на С2 байт, и строка 3 - на Сз байт. Значения сдвигов С1, С2 и С3 в Rijndael зависят от длины блока Nb .

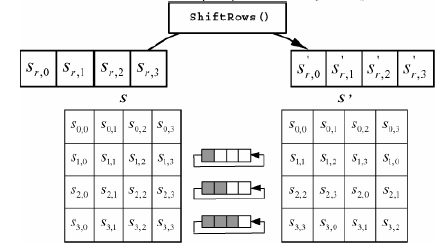
Рисунок 1.11 «Преобразование сдвига строк в функции зашифрования»

В преобразовании обратного сдвига строк InvShiftRows последние 3 строки состояния циклически сдвигаются ВПРАВО на различное число байтов. Строка 1 сдвигается на С1байт, строка 2 - на С2 байт, и строка 3 - на С3 байт.

Перемешивание столбцов

В преобразовании перемешивания столбцов (MixColumns) столбцы состояния рассматриваются как многочлены над GF(2S) и подвергаются преобразованию /j,(g) = с * gmod(Y4 +1), где с = (Х,1,1,Х +1), т.е умножаются по модулю х4 + 1 на многочлен с(х), выглядящий, как: с(х) = {03}х3 + {01}х2 + {01}х + {02}.

Это преобразование может быть представлено в матричном виде следующим образом:

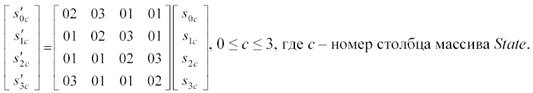
Применение этой операции ко всем четырем столбцам состояния обозначается, как MixColumns(State). Рисунок 1.13 демонстрирует применение преобразования MixColumnsQ к столбцу состояния.

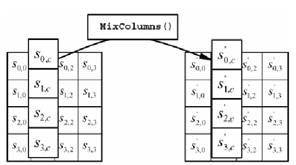
Рисунок 1.13. «Операция перемешивания действует на столбцы состояния»

В обратном преобразовании InvMixColumnsQ столбцы состояния рассматриваются как многочлены над GF(2S), но, естественно, подвергаются обратному преобразованию v(g) = ^-1(g) = d-gmod(Y4+l), где d = (Х3+Х2 + Х,Х3+l,X3+X2+l,X3+X + 1), т.е умножаются по модулю х4 + 1 на многочлен d(x), выглядящий следующим образом: d(x) = {Ob}x3 + {0d}x2 + {09}х + {0e}.

Это может быть представлено в матричном виде следующим образом:

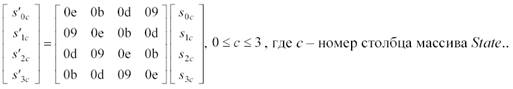
Добавление раундового ключа AddRoundKey()

В данной операции раундовый ключ добавляется к состоянию посредством поразрядного XOR. Длина ключа (в 32-разрядных словах) равна длине блока Nb .

Рисунок 1.14 иллюстрирует действие данной операции на состояние. Это преобразование обозначается как AddRoundKey(State, RoundKey).

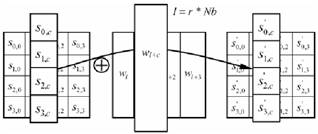
Основные особенности AES

В заключении сформулируем основные особенности AES:

новая архитектура «Квадрат», обеспечивающая быстрое рассеивание и перемеши вание информации, при этом за один раунд преобразованию подвергается весь входной блок;

байт-ориентированная структура, удобная для реализация на 8-разрядных микро контроллерах;

• все раундовые преобразования суть операции в конечных полях, допускающие эффективную аппаратную и программную реализацию на различных платформах