Федеральное агентство по образованию.
Государственное образовательное учреждение высшего профессионального
образования.
Самарский государственный технический университет.
Кафедра: «Технология органического и нефтехимического синтеза»
Курсовой проект по дисциплине:«Расчеты и прогнозирование свойств органических соединений»
Выполнил:
Руководитель:
Самара 2008 г.
Задание 19А
на курсовую работу по дисциплине "Расчеты и прогнозирование свойств органических соединений"
1) Для четырех соединений, приведенных в таблице, вычислить ![]() ,
, ![]() ,
, ![]() методом Бенсона по атомам с учетом первого окружения.
методом Бенсона по атомам с учетом первого окружения.
2) Для первого соединения рассчитать ![]() и
и ![]() .
.
3) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить критическую (жидкость-пар) температуру, критическое давление, критический объем, ацентрический фактор.
4) Для первого соединения рассчитать ![]() ,
, ![]() ,
, ![]() . Определить фазовое состояние компонента.
. Определить фазовое состояние компонента.
5) Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента.
6) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить плотность насыщенной жидкости. Привести графические зависимости "плотность-температура" для области сосуществования жидкой и паровой фаз. Выполнить их анализ.
7) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить давление насыщенного пара. Привести графические Р-Т зависимости для области сосуществования жидкой и паровой фаз. Выполнить их проверку и анализ.
8) Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить ![]() и
и ![]() . Привести графические зависимости указанных энтальпий испарения от температуры для области сосуществования жидкой и паровой фаз. Выполнить их анализ.
. Привести графические зависимости указанных энтальпий испарения от температуры для области сосуществования жидкой и паровой фаз. Выполнить их анализ.
9) Для первого соединения рассчитать рекомендованными методами вязкость вещества при температуре 730 К и низком давлении.
10) Для первого соединения рассчитать рекомендованными методами вязкость вещества при температуре 730 К и давлении 100 атм.
11) Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730 К и низком давлении.
12) Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730 К и давлении 100 атм.
Задание №1
Для четырех соединений, приведенных в таблице, рассчитать ![]()
![]() и
и ![]() методом Бенсона с учетом первого окружения.
методом Бенсона с учетом первого окружения.
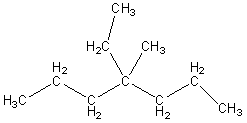
3,4,4-Триметилгептан
Из таблицы Бенсона возьмем парциальные вклады для ![]()
![]() и
и ![]() , вводим набор поправок:
, вводим набор поправок:
поправки на гош взаимодействие
R=C6H13
R1=C2H5, R2=C3H7
Вводим 7 поправок «алкил-алкил»
Поправка на симметрию:
![]() ,
, ![]()
Поправка на смешение конформеров:
![]()
Таблица 1
|
| Кол-во вкладов | Вклад | Вклад в энтальпию, кДж/моль | Вклад | Вклад в энтропию Дж/К*моль | Вклад | Вклад в т/емкость Дж/К*моль |
| СН3-(С) | 5 | -42.19 | -210.95 | 127.29 | 636.45 | 25.910 | 129.55 |
| СН-(3С) | 1 | -7.95 | -7.95 | -50.52 | -50.52 | 19.000 | 19 |
| С-(4С) | 1 | 2.09 | 2.09 | -146.92 | -146.92 | 18.29 | 18.29 |
| СН2-(2С) | 3 | -20.64 | -61.92 | 39.43 | 118.29 | 23.02 | 69.06 |
| ∑ | 10 | -278.73 | 557.3 | 235.9 | |||
| гош-поправка | 7 | 3.35 | 23.45 | для вкладов в энтропию и теплоемкость для данной поправки в справочке не приведены значения | |||
| поправка на симм. | σнар=1 |
| σвнутр=243 |
| -45.669 |
|
|
| попр. на смешение | N= | 1 |
|
| 5.76 |
|
|
|
|
| ΔHo | -255.28 | ΔSo | 517.391 | ΔСpo | 235.9 |
Рассчитаем для этого соединения энтальпию и энтропию образования методом Татевского по связям по первому уровню приближения.
|
| Кол-во вкладов | Парц. вклад, кДж/моль | Вклад в энтальпию кДж/моль | Парц. вклад, Дж/К*моль | Вклад в энтропию Дж/К*моль |
| (С1-С2)1 | 2 | -52,581 | -105,162 | 147,74 | 295,48 |
| (С1-С3)1 | 1 | -45,286 | -45,286 | 111,08 | 111,08 |
| (С1-С4)1 | 2 | -41,286 | -82,572 | 92,46 | 184,92 |
| (С2-С3)1 | 2 | -10,686 | -21,372 | 0,41 | 0,82 |
| (С3-С4)1 | 2 | 13,362 | 26,724 | -63,04 | -126,08 |
| ∑ | 9 |
| -227,668 |
| 466,22 |
| ΔHo | -227,668 | ΔSo | 466,220 |
Циклогексан
Из таблицы Бенсона возьмем парциальные вклады для ![]()
![]() и
и ![]() , вводим набор поправок: Поправки на гош – взаимодействие отсутствуют.
, вводим набор поправок: Поправки на гош – взаимодействие отсутствуют.
Вводим поправку на циклогексановый цикл.
Таблица 2
|
| Кол-во вкладов | Вклад | Вклад в энтальпию, кДж/моль | Вклад | Вклад в энтропию Дж/К*моль | Вклад | Вклад в т/емкость Дж/К*моль |
| СН2-(2С) | 6 | -20.64 | -123.84 | 39.43 | 236.58 | 23.02 | 138.12 |
| поправка на цикл | 1 |
|
| 78.69 | 78.69 | -24.28 | -24.28 |
| ∑ | 6 |
| -123.84 |
| 315.27 |
| 113.84 |
|
|
| ΔHo | -123.84 | So | 315.270 | Сpo | 113.840 |
Рассчитаем для этого соединения энтальпию и энтропию образования методом Татевского по связям по первому уровню приближения.
| Кол-во вкладов | Парц. вклад, кДж/моль | Вклад в энтальпиюкДж/моль | Парц. вклад, Дж/К*моль | Вклад в энтропию Дж/К*моль | |
| (С2-С2)1 | 6 | -20,628 | -123,768 | 39,03 | 234,18 |
| ∑ | 6 |
| -123,768 |
| 234,18 |
| поправка на цикл | 76,89 | ||||
|
|
| ΔHo | -123,768 | ΔSo | 311,070 |
Этилнонаноат
Из таблицы Бенсона возьмем парциальные вклады для ![]()
![]() и
и ![]() , вводим набор поправок.
, вводим набор поправок.
Поправки на гош – взаимодействие:
Вводим 1 поправку «алкил-алкил». Поправка на внутреннюю симметрию: ![]() .
.
![]()
Таблица 3
|
| Кол-во вкла-дов | Вклад | Вклад в энтальпию, кДж/моль | Вклад | Вклад в энтропию Дж/К*моль | Вклад | Вклад в т/емкость Дж/К*моль | |
| СН3-(С) | 2 | -42.19 | -84.38 | 127.29 | 254.58 | 25.91 | 51.82 |
|
| О-(С,С0) | 1 | -180.41 | -180.41 | 35.12 | 35.12 | 11.64 | 11.64 |
|
| СН2-(С,О) | 1 | -33.91 | -33.91 | 41.02 | 41.02 | 20.89 | 20.89 |
|
| СО-(С,О) | 1 | -146.86 | -146.86 | 20 | 20 | 24.98 | 24.98 |
|
| СН2-(2С) | 6 | -20.64 | -123.84 | 39.43 | 236.58 | 23.02 | 138.12 |
|
| СН2-(С,СО) | 1 | -21.77 | -21.77 | 40.18 | 40.18 | 25.95 | 25.95 |
|
| ∑ | 12 |
| -591.17 |
| 627.48 |
| 273.4 |
|
| поправка на симм. | σнар=1 |
| σвнутр=9 |
| -18.268 |
|
| |
|
|
| ΔHo | -591.17 | So | 609.212 | Сpo | 273.400 | |
орто-Толуидин
Из таблицы Бенсона возьмем парциальные вклады для ![]()
![]() и
и ![]() , вводим набор поправок. Поправка на симметрию:
, вводим набор поправок. Поправка на симметрию:
![]()
![]()
Введем поправку на орто-взаимодействие типа «полярный/неполярный»
Таблица 4
|
| Кол-во вкла-дов | Вклад | Вклад в энтальпию, кДж/моль | Вклад | Вклад в энтропию Дж/К*моль | Вклад | Вклад в т/емкость Дж/К*моль |
| СН3-(Сb) | 1 | -42.19 | -42.19 | 127.29 | 127.29 | 13.56 | 13.56 |
| NН2-(Сb) | 1 | 20.09 | 20.09 | 124.36 | 124.36 | 15.03 | 15.03 |
| Cb-C | 1 | 23.06 | 23.06 | -32.19 | -32.19 | 11.18 | 11.18 |
| Cb-N | 1 | -2.09 | -2.09 | 40.56 | 40.56 | 18.42 | 18.42 |
| Cb-H | 4 | 13.81 | 55.24 | 48.26 | 193.04 | 17.16 | 68.64 |
| ∑ | 8 |
| 54.11 |
| 453.06 |
| 126.83 |
| орто-поправка | 1 |
| 1.42 |
|
|
|
|
| поправка на симм. | σнар=1 |
| σвнутр=3 |
| -9.134 |
|
|
|
|
| ΔHo | 55.53 | So | 443.926 | Сpo | 126.830 |
Рассчитаем для этого соединения энтальпию и энтропию образования методом Татевского по связям по второму уровню приближения.
| Кол-во вкладов | Парц. вклад, кДж/моль | Вклад в энтальпию кДж/моль | |
| (Cb-H)1 | 4 | 13,877 | 55,508 |
| Cb-NH2 | 1 | 18,42 | 18,42 |
| (Cb-C1)1 | 1 | -19,121 | -19,121 |
| ∑ | 6 |
| 54,807 |
|
| ΔHo | 54,807 |
Задание №2
Для первого соединения рассчитать ![]() и
и ![]()
3,4,4-Триметилгептан
Энтальпия.
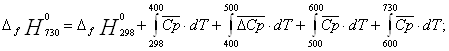
где ![]() -энтальпия образования вещества при 730К;
-энтальпия образования вещества при 730К; ![]() -энтальпия образования вещества при 298К;
-энтальпия образования вещества при 298К; ![]() -средняя теплоемкость.
-средняя теплоемкость.
![]() ;
;
![]()
Для расчета из таблицы Бенсона выпишем парциальные вклады ![]() соответственно для 298К, 400К, 500К, 600К, 800К и путем интерполяции найдем
соответственно для 298К, 400К, 500К, 600К, 800К и путем интерполяции найдем ![]() для 730К., и
для 730К., и ![]() для элементов составляющих соединение.
для элементов составляющих соединение.
Таблица 5
|
| Кол-во вкладов | Сpi, 298K, | Сpi, 400K, | Сpi, 500K, | Сpi, 600K, | Сpi, 730K, | Сpi, 800K, |
| ||||||||
| СН3-(С) | 5 | 25.910 | 32.820 | 39.950 | 45.170 | 51.235 | 54.5 |
| ||||||||
| СН-(3С) | 1 | 19.000 | 25.120 | 30.010 | 33.700 | 37.126 | 38.97 |
| ||||||||
| С-(4С) | 1 | 18.29 | 25.66 | 30.81 | 33.99 | 35.758 | 36.71 |
| ||||||||
| СН2-(2С) | 3 | 23.02 | 29.09 | 34.53 | 39.14 | 43.820 | 46.34 |
| ||||||||
| ∑ | 10 | 235.900 | 302.150 | 364.160 | 410.960 | 460.516 |
|
| ||||||||
| С | 10 | 28.836 | 29.179 | 29.259 | 29.321 | 29.511 | 29.614 | ||||||||
| Н2 | 11 | 403.636 | 440.259 | 468.119 | 491.151 | 512.824 | |||||||||
| ∑ |
| 28.836 | 29.179 | 29.259 | 29.321 | 29.511 | 29.614 | ||||||||
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Энтропия.
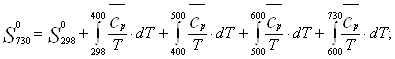
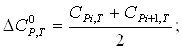
Для расчета из таблицы Бенсона выпишем парциальные вклады ![]() соответственно для 298К, 400К, 500К, 600К, 800К и путем интерполяции найдем
соответственно для 298К, 400К, 500К, 600К, 800К и путем интерполяции найдем ![]() для 730К.
для 730К.
Таблица 5
|
| Кол-во вкладов | Сpi, 298K, | Сpi, 400K, | Сpi, 500K, | Сpi, 600K, | Сpi, 730K, | Сpi, 800K, |
| СН3-(С) | 5 | 25.910 | 32.820 | 39.950 | 45.170 | 51.235 | 54.5 |
| СН-(3С) | 1 | 19.000 | 25.120 | 30.010 | 33.700 | 37.126 | 38.97 |
| С-(4С) | 1 | 18.29 | 25.66 | 30.81 | 33.99 | 35.758 | 36.71 |
| СН2-(2С) | 3 | 23.02 | 29.09 | 34.53 | 39.14 | 43.820 | 46.34 |
| ∑ | 10 | 235.900 | 302.150 | 364.160 | 410.960 | 460.516 |
|
![]()
![]()
![]()
![]()
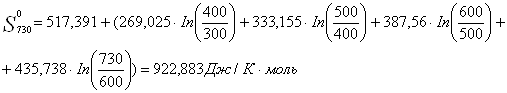
Задание №3
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить (жидкость-пар) температуру, критическое давление, критический объем, ацентрический фактор.
Метод Лидерсена.
Критическую температуру находим по формуле:
![]()
где ![]() -критическая температура;
-критическая температура; ![]() -температура кипения (берем из таблицы данных);
-температура кипения (берем из таблицы данных); ![]() -сумма парциальных вкладов в критическую температуру.
-сумма парциальных вкладов в критическую температуру.
Критическое давление находится по формуле:
![]()
где ![]() -критическое давление;
-критическое давление; ![]() -молярная масса вещества;
-молярная масса вещества; ![]() -сумма парциальных вкладов в критическое давление.
-сумма парциальных вкладов в критическое давление.
Критический объем находим по формуле:
![]()
где ![]() -критический объем;
-критический объем; ![]() -сумма парциальных вкладов в критический объем.
-сумма парциальных вкладов в критический объем.
Ацентрический фактор рассчитывается по формуле:
![]() ;
;
где ![]() -ацентрический фактор;
-ацентрический фактор; ![]() -критическое давление, выраженное в физических атмосферах;
-критическое давление, выраженное в физических атмосферах; ![]()
![]() -приведенная нормальная температура кипения вещества;
-приведенная нормальная температура кипения вещества;
![]() -нормальная температура кипения вещества в градусах Кельвина;
-нормальная температура кипения вещества в градусах Кельвина;
![]() -критическая температура в градусах Кельвина.
-критическая температура в градусах Кельвина.
Для расчета, выбираем парциальные вклады для каждого вещества из таблицы составляющих для определения критических свойств по методу Лидерсена.
3,4,4-Триметилгептан
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP | ΔV |
| СН3-(С) | 5 | 0.1 | 1.135 | 275 |
| СН2-(2С) | 3 | 0.06 | 0.681 | 165 |
| СН-(3С) | 1 | 0.012 | 0.21 | 51 |
| С-(4С) | 1 | 0 | 0.21 | 41 |
| ∑ | 10 | 0.172 | 2.236 | 532 |
Критическая температура.
![]()
![]()
Критическое давление.
![]()
![]() .
. ![]()
Критический объем.
![]()
Ацентрический фактор.
Поскольку для вещества отсутствуют экспериментальные значения критических параметров, используем параметры, полученные методом Лидерсена.
![]() ;
; ![]()
![]()
![]()
![]()
Циклогексан
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | к-во |
|
|
| |||
| (CH2)цикл | 6 | 0.078 | 1.104 | 267 | |||
| Сумма | 6 | 0.078 | 1.104 | 267 |
Критическая температура.
![]()
![]()
Критическое давление.
![]()
![]()
Критический объем.
![]()
Ацентрический фактор.
![]()
![]()
![]()
![]()
![]()
Этилнонаноат
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP | ΔV |
| CН3 | 2 | 0.04 | 0.454 | 110 |
| CH2 | 8 | 0.16 | 1.816 | 440 |
| -CОО- | 1 | 0.047 | 0.47 | 80 |
| Сумма | 11 | 0.247 | 2.74 | 630 |
Критическая температура.
![]()
![]()
![]()
Критическое давление.
![]() ;
; ![]()
Критический объем.
![]()
Ацентрический фактор.
![]()
![]()
![]()
![]()
![]()
орто-Толуидин
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP | ΔV |
| СН3- | 1 | 0.02 | 0.227 | 55 |
| -CH= (цикл.) | 4 | 0.044 | 0.616 | 148 |
| >C= (цикл.) | 2 | 0.022 | 0.308 | 72 |
| NH2 - | 1 | 0.031 | 0.095 | 28 |
| Сумма | 8 | 0.117 | 1.246 | 303 |
Критическая температура.
![]()
![]()
Критическое давление.
![]()
![]()
Критический объем.
![]()
Ацентрический фактор.
![]()
![]()
![]()
![]()
![]() .
.
Метод Джобака.
Критическую температуру находим по уравнению;
![]()
где ![]() -критическая температура;
-критическая температура; ![]() -температура кипения (берем из таблицы данных);
-температура кипения (берем из таблицы данных);
![]() -количество структурных фрагментов в молекуле;
-количество структурных фрагментов в молекуле; ![]() -парциальный вклад в свойство.
-парциальный вклад в свойство.
Критическое давление находим по формуле:
![]()
где ![]() -критическое давление в барах;
-критическое давление в барах; ![]() -общее количество атомов в молекуле;
-общее количество атомов в молекуле; ![]()
![]() -количество структурных фрагментов;
-количество структурных фрагментов; ![]() -парциальный вклад в свойство.
-парциальный вклад в свойство.
Критический объем находим по формуле:
![]()
где ![]() -критический объем в
-критический объем в ![]() ;
; ![]()
![]() -количество структурных фрагментов;
-количество структурных фрагментов; ![]() -парциальный вклад в свойство.
-парциальный вклад в свойство.
Для расчета, выбираем парциальные вклады в различные свойства для каждого вещества из таблицы составляющих для определения критических свойств по методу Джобака.
3,4,4-Триметилгептан
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP | ΔV |
| СН3- | 5 | 0.0705 | -0.006 | 325 |
| ,-СН2- | 3 | 0.0567 | 0 | 168 |
| >СН- | 1 | 0.0164 | 0.002 | 41 |
| >С< | 1 | 0.0067 | 0.0043 | 27 |
| ∑ | 10 | 0.1503 | 0.0003 | 561 |
Критическая температура.
![]()
![]()
Критическое давление.
![]() ;
; ![]()
Циклогексан
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | к-во | ΔT | ΔP | ΔV |
| (CH2)цикл | 6 | 0.06 | 0.015 | 288 |
| Сумма | 6 | 0.06 | 0.015 | 288 |
Критическая температура.
![]()
![]()
Критическое давление.
![]() ;
; ![]()
Этилнонаноат
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP |
| CН3 | 2 | 0.0282 | -0.0024 |
| CH2 | 8 | 0.1512 | 0 |
| -CОО- | 1 | 0.0481 | 0.0005 |
| Сумма | 11 | 0.2275 | -0.0019 |
Критическая температура.
![]()
![]()
![]()
Критическое давление.
![]() ;
; ![]()
орто-Толуидин
Выпишем парциальные вклады для температуры, давления и объема:
| Группа | кол-во | ΔT | ΔP |
| СН3- | 3 | 0.0423 | -0.0036 |
| (=CH)(ds) | 3 | 0.0246 | 0.0033 |
| (=C)(ds) | 2 | 0.0286 | 0.0016 |
| NH2 | 1 | 0.0243 | 0.0109 |
| Сумма | 9 | 0.1198 | 0.0122 |
Критическая температура.
![]()
![]()
Критическое давление.
![]() ;
; ![]()
Задание №4
Для первого соединения рассчитать ![]() ,
, ![]() и
и ![]() . Определить фазовое состояние компонента.
. Определить фазовое состояние компонента.
Энтальпия
3,4,4-Триметилгептан
Для расчета ![]() ,
, ![]() и
и ![]() воспользуемся таблицами Ли-Кеслера и разложением Питцера.
воспользуемся таблицами Ли-Кеслера и разложением Питцера.
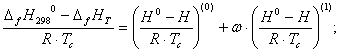
где ![]() - энтальпия образования вещества в стандартном состоянии;
- энтальпия образования вещества в стандартном состоянии; ![]() -энтальпия образования вещества в заданных условиях;
-энтальпия образования вещества в заданных условиях; 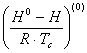 и
и 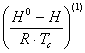 -изотермические изменения энтальпии.
-изотермические изменения энтальпии.
Находим приведенные температуру и давление:
![]()
![]()
по этим значениям с помощью таблицы Ли-Кеслера и разложения Питцера интерполяцией находим изотермическое изменение энтальпии.
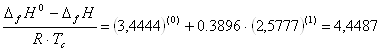
![]()
Из правой части выражаем: ![]()
![]()
Энтропия
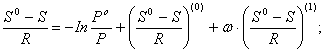
где ![]() энтропия вещества в стандартном состоянии;
энтропия вещества в стандартном состоянии; ![]() - энтропия вещества в заданных условиях;
- энтропия вещества в заданных условиях;![]() -ацентрический фактор.
-ацентрический фактор.
Критические параметры вещества определяем методом Лидерсена.
![]()
![]() ; R=8,314Дж/моль*К
; R=8,314Дж/моль*К
![]()
![]()
Находим приведенные температуру и давление:
![]()
![]()
по этим значениям с помощью таблицы Ли-Кесслера и разложения Питцера интерполяцией находим изотермическое изменение энтропии.
![]()
![]()
![]()
Теплоемкость.
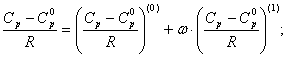
где ![]() - теплоемкость соединения при стандартных условиях;
- теплоемкость соединения при стандартных условиях; ![]() - теплоемкость соединения при заданных условиях;
- теплоемкость соединения при заданных условиях; ![]() -ацентрический фактор.
-ацентрический фактор.
Критические параметры вещества определяем методом Лидерсена.
![]()
![]() ; R=8,314Дж/моль*К
; R=8,314Дж/моль*К
![]()
![]()
Находим приведенные температуру и давление:
![]()
![]()
по этим значениям с помощью таблицы Ли-Кесслера и разложения Питцера интерполяцией находим изотермическое изменение теплоемкости.
![]()
![]() Дж/моль*К
Дж/моль*К
Из правой части выражаем:
![]()
Задание №5
Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента.
Для определения плотности вещества воспользуемся методом прогнозирования плотности индивидуальных веществ с использованием коэффициента сжимаемости.
![]()
где ![]() -плотность вещества; М- молярная масса; V-объем.
-плотность вещества; М- молярная масса; V-объем.
Для данного вещества найдем коэффициент сжимаемости с использованием таблицы Ли-Кесслера по приведенным температуре и давлении.
Коэффициент сжимаемости находится по разложению Питцера:
![]()
где Z-коэффициент сжимаемости; ![]() -ацентрический фактор.
-ацентрический фактор.
Приведенную температуру найдем по формуле ![]()
где ![]() -приведенная температура в К ; Т-температура вещества в К;
-приведенная температура в К ; Т-температура вещества в К; ![]() -критическая температура в К.
-критическая температура в К.
Приведенное давление найдем по формуле ![]() ; где
; где ![]() - приведенное; Р и
- приведенное; Р и![]() давление и критическое давление в атм. соответственно.
давление и критическое давление в атм. соответственно.
Критические температуру и давление а так же ацентрический фактор возьмем экспериментальные.
Критические параметры вещества определяем методом Лидерсена.
![]()
![]() ; R=8,314Дж/моль*К
; R=8,314Дж/моль*К
![]()
![]()
Находим приведенные температуру и давление:
![]()
![]()
Коэффициент сжимаемости найдем из разложения Питцера:
путем интерполяции находим ![]() и
и![]() .
.
![]() =0,8190;
=0,8190;
![]() =0,2356;
=0,2356;
![]()
Из уравнения Менделеева-Клайперона ![]() ,
,
где P-давление; V-объем; Z- коэффициент сжимаемости; R-универсальная газовая постоянная (R=82.04); T-температура;
выразим объем:
![]()
М=142,29 г/моль.
![]()
Фазовое состояние вещества определяем по таблицам Ли-Кесслера, по приведенным параметрам температуры и давления. Ячейка, соответствующая данным приведенным параметрам находится под линией бинодаля, следовательно данное вещество при 730К и 100 бар – газ.
Задание №6
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить плотность насыщенной жидкости. Привести графические зависимости «плотность-температура» для области существования жидкой и паровой фаз. Выполнить анализ.
Для вычисления плотности насыщенной жидкости воспользуемся методом Ганна-Ямады.
![]()
где ![]() -плотность насыщенной жидкости; М -молярная масса вещества;
-плотность насыщенной жидкости; М -молярная масса вещества; ![]() -молярный объем насыщенной жидкости.
-молярный объем насыщенной жидкости.
![]()
где ![]() -масштабирующий параметр;
-масштабирующий параметр; ![]() -ацентрический фактор;
-ацентрический фактор; ![]() и Г-функции приведенной температуры.
и Г-функции приведенной температуры.
![]()
![]()
3,4,4-Триметилгептан
![]() в промежутке температур от 298 до 475 К вычислим по формуле:
в промежутке температур от 298 до 475 К вычислим по формуле:
![]()
В промежутке температур от 475 до 588 К вычислим по формуле:
![]()
В промежутке температур от 298 до 480 К вычислим Г по формуле:
![]()
Находим масштабирующий параметр:
Полученные результаты сведем в таблицу:
| T, К | Tr | Vr(0) | Vsc | Г | Vs | ρs ,г/см3 |
| 145,1546 | 0,3 | 0,3252 | 254,7858 | 0,2646 | 82.8474 | 1,9149 |
| 169,347 | 0,35 | 0,3331 |
| 0,2585 | 84,87309 | 1,6765 |
| 193,5395 | 0,4 | 0,3421 |
| 0,2521 | 87,1724 | 1,6322 |
| 217,7319 | 0,45 | 0,3520 |
| 0,2456 | 89,67771 | 1,5866 |
| 241,9243 | 0,5 | 0,3625 |
| 0,2387 | 92,364 | 1,5405 |
| 266,1168 | 0,55 | 0,3738 |
| 0,2317 | 95,24881 | 1,4938 |
| 290,3092 | 0,6 | 0,3862 |
| 0,2244 | 98,39231 | 1,4461 |
| 314,5016 | 0,65 | 0,3999 |
| 0,2168 | 101,8972 | 1,3964 |
| 338,6941 | 0,7 | 0,4157 |
| 0,2090 | 105,9088 | 1,3435 |
| 362,8865 | 0,75 | 0,4341 |
| 0,2010 | 110,6151 | 1,2863 |
| 387,0789 | 0,8 | 0,4563 |
| 0,1927 | 116,2464 | 1,2240 |
| 411,2714 | 0,85 | 0,4883 |
| 0,1842 | 124,4013 | 1,1438 |
| 435,4638 | 0,9 | 0,5289 |
| 0,1754 | 134,749 | 1,0559 |
| 449,9793 | 0,93 | 0,5627 |
| 0,1701 | 143,3613 | 0,9925 |
| 459,6563 | 0,95 | 0,5941 |
| 0,1664 | 151,3625 | 0,9400 |
| 469,3332 | 0,97 | 0,6410 |
| 0,1628 | 163,3205 | 0,8712 |
| 474,1717 | 0,98 | 0,6771 |
| 0,1609 | 172,5171 | 0,8248 |
| 479,0102 | 0,99 | 0,7348 |
| 0,1591 | 187,2219 | 0,7600 |
Циклогексан
| T, К | Tr | Vr(0) | Vsc | Г | Vs | ρs ,г/см3 |
| 166,1627 | 0,3 | 0,3252 | 591,4223 | 0,2646 | 181,6158 | 0,4634 |
| 193,8565 | 0,35 | 0,3331 |
| 0,2585 | 186,3089 | 0,4517 |
| 221,5503 | 0,4 | 0,3421 |
| 0,2521 | 191,6258 | 0,4392 |
| 249,244 | 0,45 | 0,3520 |
| 0,2456 | 197,421 | 0,4263 |
| 276,9378 | 0,5 | 0,3625 |
| 0,2387 | 203,6421 | 0,4133 |
| 304,6316 | 0,55 | 0,3738 |
| 0,2317 | 210,3308 | 0,4001 |
| 332,3254 | 0,6 | 0,3862 |
| 0,2244 | 217,6231 | 0,3867 |
| 360,0192 | 0,65 | 0,3999 |
| 0,2168 | 225,7505 | 0,3728 |
| 387,7129 | 0,7 | 0,4157 |
| 0,2090 | 235,0407 | 0,3581 |
| 415,4067 | 0,75 | 0,4341 |
| 0,2010 | 245,9186 | 0,3422 |
| 443,1005 | 0,8 | 0,4563 |
| 0,1927 | 258,9074 | 0,3251 |
| 470,7943 | 0,85 | 0,4883 |
| 0,1842 | 277,5871 | 0,3032 |
| 498,4881 | 0,9 | 0,5289 |
| 0,1754 | 301,2526 | 0,2794 |
| 515,1043 | 0,93 | 0,5627 |
| 0,1701 | 320,8825 | 0,2623 |
| 526,1818 | 0,95 | 0,5941 |
| 0,1664 | 339,0594 | 0,2482 |
| 537,2594 | 0,97 | 0,6410 |
| 0,1628 | 366,1384 | 0,2299 |
| 542,7981 | 0,98 | 0,6771 |
| 0,1609 | 386,9111 | 0,2175 |
| 548,3369 | 0,99 | 0,7348 |
| 0,1591 | 420,0599 | 0,2004 |
Этилнонаноат
| T, К | Tr | Vr(0) | Vsc | Г | Vs | ρs ,г/см3 |
| 202,2 | 0,3 | 0,3252 | 632,1063 | 0,2646 | 171,6056 | 1,0856 |
| 235,9 | 0,35 | 0,3331 |
| 0,2585 | 176,6025 | 1,0549 |
| 269,6 | 0,4 | 0,3421 |
| 0,2521 | 182,2422 | 1,0222 |
| 303,3 | 0,45 | 0,3520 |
| 0,2456 | 188,3933 | 0,9889 |
| 337 | 0,5 | 0,3625 |
| 0,2387 | 195,0121 | 0,9553 |
| 370,7 | 0,55 | 0,3738 |
| 0,2317 | 202,1446 | 0,9216 |
| 404,4 | 0,6 | 0,3862 |
| 0,2244 | 209,929 | 0,8874 |
| 438,1 | 0,65 | 0,3999 |
| 0,2168 | 218,5978 | 0,8522 |
| 471,8 | 0,7 | 0,4157 |
| 0,2090 | 228,4812 | 0,8154 |
| 505,5 | 0,75 | 0,4341 |
| 0,2010 | 240,0097 | 0,7762 |
| 539,2 | 0,8 | 0,4563 |
| 0,1927 | 253,7176 | 0,7343 |
| 572,9 | 0,85 | 0,4883 |
| 0,1842 | 273,1566 | 0,6820 |
| 606,6 | 0,9 | 0,5289 |
| 0,1754 | 297,7048 | 0,6258 |
| 626,82 | 0,93 | 0,5627 |
| 0,1701 | 317,9245 | 0,5860 |
| 640,3 | 0,95 | 0,5941 |
| 0,1664 | 336,5187 | 0,5536 |
| 653,78 | 0,97 | 0,6410 |
| 0,1628 | 364,0321 | 0,5118 |
| 660,52 | 0,98 | 0,6771 |
| 0,1609 | 385,0244 | 0,4839 |
| 667,26 | 0,99 | 0,7348 |
| 0,1591 | 418,3813 | 0,4453 |
орто-Толуидин
| T, К | Tr | Vr(0) | Vsc | Г | Vs | ρs ,г/см3 |
| 208,2 | 0,3 | 0,3252 | 373,4859 | 0,2646 | 107,2399 | 0,9992 |
| 242,9 | 0,35 | 0,3331 |
| 0,2585 | 110,1973 | 0,9724 |
| 277,6 | 0,4 | 0,3421 |
| 0,2521 | 113,5407 | 0,9438 |
| 312,3 | 0,45 | 0,3520 |
| 0,2456 | 117,1863 | 0,9144 |
| 347 | 0,5 | 0,3625 |
| 0,2387 | 121,1049 | 0,8848 |
| 381,7 | 0,55 | 0,3738 |
| 0,2317 | 125,3235 | 0,8550 |
| 416,4 | 0,6 | 0,3862 |
| 0,2244 | 129,9254 | 0,8248 |
| 451,1 | 0,65 | 0,3999 |
| 0,2168 | 135,052 | 0,7934 |
| 485,8 | 0,7 | 0,4157 |
| 0,2090 | 140,9036 | 0,7605 |
| 520,5 | 0,75 | 0,4341 |
| 0,2010 | 147,7407 | 0,7253 |
| 555,2 | 0,8 | 0,4563 |
| 0,1927 | 155,8855 | 0,6874 |
| 589,9 | 0,85 | 0,4883 |
| 0,1842 | 167,5077 | 0,6397 |
| 624,6 | 0,9 | 0,5289 |
| 0,1754 | 182,2059 | 0,5881 |
| 645,42 | 0,93 | 0,5627 |
| 0,1701 | 194,3504 | 0,5514 |
| 659,3 | 0,95 | 0,5941 |
| 0,1664 | 205,5534 | 0,5213 |
| 673,18 | 0,97 | 0,6410 |
| 0,1628 | 222,1809 | 0,4823 |
| 680,12 | 0,98 | 0,6771 |
| 0,1609 | 234,8985 | 0,4562 |
| 687,06 | 0,99 | 0,7348 |
| 0,1591 | 255,146 | 0,4200 |
Задание №7
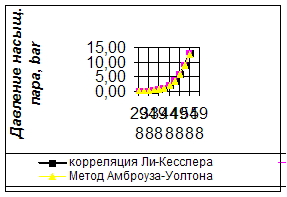
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить давление насыщенного пара. Привести графические P-T зависимости для области существования жидкой и паровой фаз. Выполнить анализ.
Для вычисления давления насыщенного пара воспользуемся корреляциями
Ли-Кесслера, Риделя и Амброуза-Уолтона.
3,4,4-Триметилгептан
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.
![]()
![]()
![]()
Давление Pvpопределяем из приведенного давления насыщенных паров Pvp,r и критического давления данного вещества. Критическое давление определяем методом Лидерсена, поскольку для данного вещества экспериментальные данные отсутствуют.
| Т | Тr | f(0) | f(1) | Pvp,r | Pvp, bar |
| 298 | 0.62 | -3.2426 | -3.4212 | 0.0103 | 0.2209 |
| 323 | 0.67 | -2.5715 | -2.5126 | 0.0287 | 0.6157 |
| 348 | 0.72 | -2.0027 | -1.8062 | 0.0668 | 1.4317 |
| 373 | 0.77 | -1.5153 | -1.2564 | 0.1347 | 2.8880 |
| 398 | 0.82 | -1.0934 | -0.8297 | 0.2425 | 5.2005 |
| 423 | 0.87 | -0.7251 | -0.5007 | 0.3984 | 8.5437 |
| 448 | 0.93 | -0.4012 | -0.2505 | 0.6073 | 13.0216 |
| 473 | 0.98 | -0.1144 | -0.0640 | 0.8699 | 18.6535 |
Корреляция Риделя
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Где ![]() приведенная температура кипения.
приведенная температура кипения.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Т | Тr | Pvp,r | Pvp, bar |
| 298 | 0,62 | 0,0084 | 0,1802 |
| 323 | 0,67 | 0,0233 | 0,4989 |
| 348 | 0,72 | 0,0541 | 1,1605 |
| 373 | 0,77 | 0,1101 | 2,3605 |
| 398 | 0,82 | 0,2019 | 4,3301 |
| 423 | 0,87 | 0,3423 | 7,3405 |
| 448 | 0,93 | 0,5471 | 11,7318 |
| 473 | 0,98 | 0,8385 | 17,9804 |
Метод Амброуза-Уолтона.
![]()
![]()
![]()
![]()
где ![]()
| Т | Тr | τ | f(0) | f(1) | f(2) | Pvp,r | Pvp, bar |
| 298 | 0,62 | 0,38 | -3,3292 | -3,6131 | -0,0601 | 0,0087 | 0,1862 |
| 323 | 0,67 | 0,33 | -2,6673 | -2,7485 | -0,0168 | 0,0237 | 0,5090 |
| 348 | 0,72 | 0,28 | -2,1019 | -2,0668 | 0,0067 | 0,0547 | 1,1726 |
| 373 | 0,77 | 0,23 | -1,6118 | -1,5198 | 0,0146 | 0,1106 | 2,3717 |
| 398 | 0,82 | 0,18 | -1,1810 | -1,0733 | 0,0116 | 0,2024 | 4,3402 |
| 423 | 0,87 | 0,13 | -0,7973 | -0,7022 | 0,0028 | 0,3428 | 7,3512 |
| 448 | 0,93 | 0,07 | -0,4509 | -0,3873 | -0,0061 | 0,5473 | 11,7360 |
| 473 | 0,98 | 0,02 | -0,1327 | -0,1120 | -0,0069 | 0,8375 | 17,9576 |
Циклогексан
Корреляция Ли-Кеслера
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.
![]()
![]()
![]()
Давление Pvpопределяем из приведенного давления насыщенных паров Pvp,r и экспериментального критического давления данного вещества, bar.
| Т | Тr | f(0) | f(1) | Pvp,r | Pvp, bar |
| 298 | 0.54 | -4.5073 | -5.3098 | 0.0036 | 0.1448 |
| 323 | 0.58 | -3.7270 | -4.1202 | 0.0100 | 0.4072 |
| 348 | 0.63 | -3.0649 | -3.1736 | 0.0237 | 0.9659 |
| 373 | 0.67 | -2.4968 | -2.4162 | 0.0492 | 2.0033 |
| 398 | 0.72 | -2.0045 | -1.8083 | 0.0917 | 3.7306 |
| 423 | 0.76 | -1.5743 | -1.3199 | 0.1564 | 6.3651 |
| 448 | 0.81 | -1.1954 | -0.9283 | 0.2483 | 10.1053 |
| 473 | 0.85 | -0.8597 | -0.6158 | 0.3713 | 15.1107 |
| 498 | 0.90 | -0.5602 | -0.3684 | 0.5280 | 21.4882 |
| 523 | 0.94 | -0.2918 | -0.1752 | 0.7195 | 29.2856 |
| 548 | 0.99 | -0.0500 | -0.0272 | 0.9457 | 38.4919 |
Корреляция Риделя.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() приведенная температура кипения.
приведенная температура кипения.
| А | В | С | D | θ | αc | ψ |
| 9,03058 | 9,28859 | -3,9997 | 0,25802 | -0,258 | 6,83696 | 2,462155 |
| Т | Тr | Pvp,r | Pvp, bar |
| 298 | 0,54 | 0.0032 | 0.1310 |
| 323 | 0,58 | 0.0089 | 0.3621 |
| 348 | 0,63 | 0.0208 | 0.8481 |
| 373 | 0,67 | 0.0428 | 1.7439 |
| 398 | 0,72 | 0.0795 | 3.2347 |
| 423 | 0,76 | 0.1358 | 5.5260 |
| 448 | 0,81 | 0.2172 | 8.8392 |
| 473 | 0,85 | 0.3296 | 13.4166 |
| 498 | 0,90 | 0.4801 | 19.5413 |
| 523 | 0,94 | 0.6775 | 27.5738 |
| 548 | 0,99 | 0.9340 | 38.0135 |
Корреляция Амброуза-Уолтона.
![]()
![]()
![]()
![]()
где ![]()
| Т | Тr | τ | f(0) | f(1) | f(2) | Pvp,r | Pvp, bar |
| 298 | 0.54 | 0.46 | -4.5713 | -5.4122 | -0.1698 | 0.0032 | 0.1319 |
| 323 | 0.58 | 0.42 | -3.8054 | -4.2768 | -0.0989 | 0.0089 | 0.3625 |
| 348 | 0.63 | 0.37 | -3.1544 | -3.3780 | -0.0473 | 0.0207 | 0.8438 |
| 373 | 0.67 | 0.33 | -2.5933 | -2.6563 | -0.0129 | 0.0424 | 1.7272 |
| 398 | 0.72 | 0.28 | -2.1037 | -2.0688 | 0.0066 | 0.0785 | 3.1969 |
| 423 | 0.76 | 0.24 | -1.6715 | -1.5842 | 0.0143 | 0.1342 | 5.4627 |
| 448 | 0.81 | 0.19 | -1.2860 | -1.1791 | 0.0131 | 0.2151 | 8.7556 |
| 473 | 0.85 | 0.15 | -0.9386 | -0.8360 | 0.0065 | 0.3275 | 13.3283 |
| 498 | 0.90 | 0.10 | -0.6223 | -0.5409 | -0.0020 | 0.4782 | 19.4646 |
| 523 | 0.94 | 0.06 | -0.3312 | -0.2824 | -0.0079 | 0.6759 | 27.5095 |
| 548 | 0.99 | 0.01 | -0.0587 | -0.0495 | -0.0041 | 0.9329 | 37.9709 |
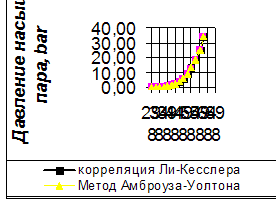
Этилнонаноат
Корреляция Ли-Кесслера.
Корреляция Ли-Кесслера.
Она основана на использовании принципа соответственных состояний.
![]()
![]()
![]()
Давление Pvpопределяем из приведенного давления насыщенных паров Pvp,r и экспериментального критического давления данного вещества, bar.
| Т | Тr | f(0) | f(1) | Pvp,r | Pvp, bar |
| 298 | 0.44 | -6.7350 | -9.0416 | 0.0000 | 0.0001 |
| 323 | 0.48 | -5.7653 | -7.3645 | 0.0000 | 0.0007 |
| 348 | 0.52 | -4.9412 | -6.0010 | 0.0002 | 0.0037 |
| 373 | 0.55 | -4.2329 | -4.8831 | 0.0007 | 0.0148 |
| 398 | 0.59 | -3.6182 | -3.9603 | 0.0024 | 0.0480 |
| 423 | 0.63 | -3.0803 | -3.1948 | 0.0066 | 0.1312 |
| 448 | 0.66 | -2.6059 | -2.5573 | 0.0155 | 0.3108 |
| 473 | 0.70 | -2.1848 | -2.0253 | 0.0327 | 0.6550 |
| 498 | 0.74 | -1.8088 | -1.5808 | 0.0625 | 1.2506 |
| 523 | 0.78 | -1.4712 | -1.2097 | 0.1099 | 2.1977 |
| 548 | 0.81 | -1.1667 | -0.9003 | 0.1799 | 3.5983 |
| 573 | 0.85 | -0.8908 | -0.6433 | 0.2773 | 5.5456 |
| 598 | 0.89 | -0.6397 | -0.4310 | 0.4056 | 8.1123 |
| 623 | 0.92 | -0.4105 | -0.2571 | 0.5672 | 11.3430 |
| 648 | 0.96 | -0.2004 | -0.1162 | 0.7624 | 15.2486 |
Корреляция Риделя
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() приведенная температура кипения.
приведенная температура кипения.
| А | В | С | D | θ | αc | ψ |
| 15,0009 | 15,4295 | -9,1285 | 0,4286 | -0,4286 | 8,87251 | 0,816197 |
| Т | Тr | Pvp,r | Pvp, bar |
| 298 | 0,44 | 0.0000 | 0.0001 |
| 323 | 0,48 | 0.0000 | 0.0006 |
| 348 | 0,52 | 0.0001 | 0.0029 |
| 373 | 0,55 | 0.0006 | 0.0114 |
| 398 | 0,59 | 0.0018 | 0.0367 |
| 423 | 0,63 | 0.0050 | 0.0993 |
| 448 | 0,66 | 0.0117 | 0.2343 |
| 473 | 0,70 | 0.0247 | 0.4938 |
| 498 | 0,74 | 0.0474 | 0.9479 |
| 523 | 0,78 | 0.0842 | 1.6843 |
| 548 | 0,81 | 0.1404 | 2.8081 |
| 573 | 0,85 | 0.2221 | 4.4426 |
| 598 | 0,89 | 0.3368 | 6.7356 |
| 623 | 0,92 | 0.4936 | 9.8713 |
| 648 | 0,96 | 0.7046 | 14.0926 |
Корреляция Амброуза-Уолтона.
![]()
![]()
![]()
![]()
где ![]()
| Т | Тr | τ | f(0) | f(1) | f(2) | Pvp,r | Pvp, bar |
| 298 | 0.44 | 0.56 | -6.7645 | -9.0581 | -0.3883 | 0.0000 | 0.0001 |
| 323 | 0.48 | 0.52 | -5.8078 | -7.4026 | -0.2935 | 0.0000 | 0.0006 |
| 348 | 0.52 | 0.48 | -4.9973 | -6.0773 | -0.2119 | 0.0002 | 0.0031 |
| 373 | 0.55 | 0.45 | -4.3019 | -5.0038 | -0.1440 | 0.0006 | 0.0122 |
| 398 | 0.59 | 0.41 | -3.6985 | -4.1249 | -0.0898 | 0.0019 | 0.0388 |
| 423 | 0.63 | 0.37 | -3.1695 | -3.3981 | -0.0484 | 0.0052 | 0.1041 |
| 448 | 0.66 | 0.34 | -2.7013 | -2.7913 | -0.0187 | 0.0122 | 0.2433 |
| 473 | 0.70 | 0.30 | -2.2836 | -2.2799 | 0.0007 | 0.0254 | 0.5082 |
| 498 | 0.74 | 0.26 | -1.9077 | -1.8451 | 0.0113 | 0.0484 | 0.9684 |
| 523 | 0.78 | 0.22 | -1.5672 | -1.4721 | 0.0147 | 0.0855 | 1.7109 |
| 548 | 0.81 | 0.19 | -1.2565 | -1.1492 | 0.0128 | 0.1420 | 2.8398 |
| 573 | 0.85 | 0.15 | -0.9710 | -0.8672 | 0.0073 | 0.2239 | 4.4772 |
| 598 | 0.89 | 0.11 | -0.7070 | -0.6183 | 0.0003 | 0.3383 | 6.7669 |
| 623 | 0.92 | 0.08 | -0.4610 | -0.3962 | -0.0059 | 0.4943 | 9.8860 |
| 648 | 0.96 | 0.04 | -0.2297 | -0.1948 | -0.0083 | 0.7036 | 14.0725 |
орто-Толуидин
Корреляция Ли-Кеслера.
Корреляция Ли-Кеслера.
Она основана на использовании принципа соответственных состояний.
![]()
![]()
![]()
Давление Pvpопределяем из приведенного давления насыщенных паров Pvp,r и экспериментального критического давления данного вещества, bar.
| Т | Тr | f(0) | f(1) | Pvp,r | Pvp, bar |
| 298 | 0.43 | -7.1086 | -9.7060 | 0.0000 | 0.0005 |
| 323 | 0.47 | -6.1074 | -7.9479 | 0.0001 | 0.0027 |
| 348 | 0.50 | -5.2564 | -6.5151 | 0.0003 | 0.0117 |
| 373 | 0.54 | -4.5248 | -5.3373 | 0.0011 | 0.0406 |
| 398 | 0.57 | -3.8898 | -4.3621 | 0.0031 | 0.1166 |
| 423 | 0.61 | -3.3339 | -3.5504 | 0.0077 | 0.2887 |
| 448 | 0.65 | -2.8436 | -2.8721 | 0.0168 | 0.6317 |
| 473 | 0.68 | -2.4084 | -2.3035 | 0.0333 | 1.2479 |
| 498 | 0.72 | -2.0196 | -1.8262 | 0.0603 | 2.2622 |
| 523 | 0.75 | -1.6705 | -1.4254 | 0.1017 | 3.8132 |
| 548 | 0.79 | -1.3555 | -1.0891 | 0.1611 | 6.0415 |
| 573 | 0.83 | -1.0700 | -0.8076 | 0.2420 | 9.0762 |
| 598 | 0.86 | -0.8103 | -0.5729 | 0.3473 | 13.0234 |
Корреляция Риделя
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() приведенная температура кипения.
приведенная температура кипения.
| А | В | С | D | θ | αc | ψ |
| 12,413 | 12,7677 | -6,9055 | 0,35466 | -0,3547 | 7,9902 | 1,606207 |
| Т | Тr | Pvp,r | Pvp, bar |
| 298 | 0,43 | 0.0000 | 0.0004 |
| 323 | 0,47 | 0.0001 | 0.0022 |
| 348 | 0,50 | 0.0003 | 0.0095 |
| 373 | 0,54 | 0.0009 | 0.0326 |
| 398 | 0,57 | 0.0025 | 0.0931 |
| 423 | 0,61 | 0.0061 | 0.2292 |
| 448 | 0,65 | 0.0133 | 0.5000 |
| 473 | 0,68 | 0.0263 | 0.9872 |
| 498 | 0,72 | 0.0479 | 1.7946 |
| 523 | 0,75 | 0.0812 | 3.0453 |
| 548 | 0,79 | 0.1301 | 4.8797 |
| 573 | 0,83 | 0.1988 | 7.4549 |
| 598 | 0,86 | 0.2920 | 10.9493 |
Корреляция Амброуза-Уолтона.
![]()
![]()
![]()
![]()
где ![]()
| Т | Тr | τ | f(0) | f(1) | f(2) | Pvp,r | Pvp, bar |
| 298 | 0.43 | 0.57 | -7.1342 | -9.7215 | -0.4236 | 0.0000 | 0.0004 |
| 323 | 0.47 | 0.53 | -6.1449 | -7.9754 | -0.3273 | 0.0001 | 0.0024 |
| 348 | 0.50 | 0.50 | -5.3071 | -6.5748 | -0.2430 | 0.0003 | 0.0104 |
| 373 | 0.54 | 0.46 | -4.5885 | -5.4385 | -0.1715 | 0.0009 | 0.0353 |
| 398 | 0.57 | 0.43 | -3.9652 | -4.5070 | -0.1130 | 0.0027 | 0.0995 |
| 423 | 0.61 | 0.39 | -3.4191 | -3.7358 | -0.0670 | 0.0064 | 0.2417 |
| 448 | 0.65 | 0.35 | -2.9362 | -3.0914 | -0.0326 | 0.0139 | 0.5207 |
| 473 | 0.68 | 0.32 | -2.5057 | -2.5482 | -0.0087 | 0.0271 | 1.0171 |
| 498 | 0.72 | 0.28 | -2.1188 | -2.0863 | 0.0062 | 0.0489 | 1.8331 |
| 523 | 0.75 | 0.25 | -1.7686 | -1.6903 | 0.0134 | 0.0824 | 3.0909 |
| 548 | 0.79 | 0.21 | -1.4496 | -1.3479 | 0.0145 | 0.1315 | 4.9311 |
| 573 | 0.83 | 0.17 | -1.1570 | -1.0493 | 0.0112 | 0.2003 | 7.5116 |
| 598 | 0.86 | 0.14 | -0.8869 | -0.7866 | 0.0052 | 0.2936 | 11.0098 |
Задание №8
Для четырех соединений, приведенных в таблице, рекомендованными методами вычислить ![]() и
и ![]()
3,4,4-Триметилгептан
Уравнение Ли-Кесслера.
![]() ;
;
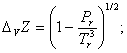 для стандартных условий
для стандартных условий ![]()
![]()
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление возьмем из задания №7 ![]() ацентрический фактор
ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,62 | 0.9777 | 8.2506 | 33189.78 | 32449.87 |
| 323 | 0,67 | 0.9505 | 7.9646 | 32039.38 | 30454.05 |
| 348 | 0,72 | 0.9058 | 7.7092 | 31011.88 | 28091.58 |
| 373 | 0,77 | 0.8402 | 7.4981 | 30162.55 | 25343.94 |
| 398 | 0,82 | 0.7512 | 7.3495 | 29564.98 | 22207.95 |
| 423 | 0,87 | 0.6354 | 7.2874 | 29315.34 | 18625.74 |
| 448 | 0,93 | 0.4847 | 7.3426 | 29537.16 | 14317.40 |
| 473 | 0,98 | 0.2623 | 7.5538 | 30386.83 | 7971.58 |
Корреляция Риделя.
![]() ;
;
![]()
 для стандартных условий
для стандартных условий ![]() ,
,
R=8.314, ![]() -возьмем из задания №3,
-возьмем из задания №3, ![]() -Возьмем из задания №7,
-Возьмем из задания №7, ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,62 | 0,9819 | 8,2422 | 33155,96 | 32554,32 |
| 323 | 0,67 | 0,9601 | 7,9668 | 32048,27 | 30769,39 |
| 348 | 0,72 | 0,9244 | 7,7217 | 31062,05 | 28713,96 |
| 373 | 0,77 | 0,8716 | 7,5203 | 30251,93 | 26367,94 |
| 398 | 0,82 | 0,7982 | 7,3807 | 29690,65 | 23699,88 |
| 423 | 0,87 | 0,6983 | 7,3267 | 29473,26 | 20581,90 |
| 448 | 0,93 | 0,5574 | 7,3885 | 29721,85 | 16568,02 |
| 473 | 0,98 | 0,3200 | 7,6046 | 30590,99 | 9790,25 |
Корреляция Амброуза-Уолтона.
![]() ;
;

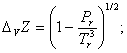 для стандартных условий
для стандартных условий ![]() ;
;
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление![]() возьмем из задания №7
возьмем из задания №7 ![]() ; ацентрический фактор
; ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | τ | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,62 | 0,38 | 0,9812 | 8,1354 | 32726,26 | 32112,18 |
| 323 | 0,67 | 0,33 | 0,9593 | 7,8663 | 31643,77 | 30355,10 |
| 348 | 0,72 | 0,28 | 0,9236 | 7,6463 | 30758,76 | 28408,55 |
| 373 | 0,77 | 0,23 | 0,8710 | 7,4771 | 30078,28 | 26196,92 |
| 398 | 0,82 | 0,18 | 0,7977 | 7,3633 | 29620,59 | 23628,24 |
| 423 | 0,87 | 0,13 | 0,6978 | 7,3159 | 29429,80 | 20535,82 |
| 448 | 0,93 | 0,07 | 0,5572 | 7,3619 | 29614,99 | 16501,90 |
| 473 | 0,98 | 0,02 | 0,3218 | 7,5954 | 30554,27 | 9832,55 |
Циклогексан
Уравнение Ли-Кеслера.
![]() ;
;
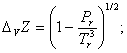 для стандартных условий
для стандартных условий ![]()
![]()
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление возьмем из задания №7 ![]() ацентрический фактор
ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,54 | 0.9885 | 7.2198 | 33224.13 | 32843.11 |
| 323 | 0,58 | 0.9745 | 7.0476 | 32431.76 | 31604.78 |
| 348 | 0,63 | 0.9511 | 6.8847 | 31681.78 | 30131.21 |
| 373 | 0,67 | 0.9161 | 6.7350 | 30993.26 | 28391.73 |
| 398 | 0,72 | 0.8680 | 6.6043 | 30391.58 | 26380.48 |
| 423 | 0,76 | 0.8060 | 6.4996 | 29909.91 | 24107.04 |
| 448 | 0,81 | 0.7292 | 6.4303 | 29590.87 | 21578.13 |
| 473 | 0,85 | 0.6365 | 6.4080 | 29488.40 | 18768.10 |
| 498 | 0,90 | 0.5245 | 6.4475 | 29669.91 | 15562.17 |
| 523 | 0,94 | 0.3835 | 6.5667 | 30218.64 | 11589.23 |
| 548 | 0,99 | 0.1597 | 6.7878 | 31236.32 | 4987.20 |
Корреляция Риделя.
![]() ;
;
![]()
 для стандартных условий
для стандартных условий ![]() ,
,
R=8.314, ![]() -возьмем из задания №3.,
-возьмем из задания №3., ![]() -Возьмем из задания №7.,
-Возьмем из задания №7., ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,54 | 0.9896 | 7.1555 | 32928.02 | 32586.80 |
| 323 | 0,58 | 0.9774 | 6.9902 | 32167.44 | 31439.15 |
| 348 | 0,63 | 0.9572 | 6.8340 | 31448.58 | 30101.43 |
| 373 | 0,67 | 0.9274 | 6.6909 | 30790.21 | 28553.53 |
| 398 | 0,72 | 0.8867 | 6.5664 | 30217.31 | 26793.58 |
| 423 | 0,76 | 0.8341 | 6.4676 | 29762.52 | 24826.39 |
| 448 | 0,81 | 0.7684 | 6.4035 | 29467.78 | 22642.73 |
| 473 | 0,85 | 0.6869 | 6.3858 | 29386.19 | 20184.18 |
| 498 | 0,90 | 0.5838 | 6.4288 | 29584.07 | 17270.38 |
| 523 | 0,94 | 0.4438 | 6.5503 | 30143.37 | 13376.91 |
| 548 | 0,99 | 0.1939 | 6.7722 | 31164.19 | 6043.21 |
Корреляция Амброуза-Уолтона.
![]() ;
;
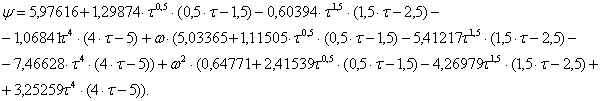
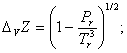 для стандартных условий
для стандартных условий ![]() ;
;
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() . приведенное давление
. приведенное давление![]() возьмем из задания №7
возьмем из задания №7 ![]() ; ацентрический фактор
; ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | τ | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,54 | 0,46 | 0.9896 | 7.1238 | 32782.15 | 32439.93 |
| 323 | 0,58 | 0,42 | 0.9773 | 6.9405 | 31938.89 | 31214.86 |
| 348 | 0,63 | 0,37 | 0.9574 | 6.7847 | 31221.82 | 29891.22 |
| 373 | 0,67 | 0,33 | 0.9281 | 6.6565 | 30631.89 | 28428.80 |
| 398 | 0,72 | 0,28 | 0.8881 | 6.5561 | 30169.69 | 26793.83 |
| 423 | 0,76 | 0,24 | 0.8362 | 6.4839 | 29837.75 | 24951.42 |
| 448 | 0,81 | 0,19 | 0.7709 | 6.4418 | 29643.81 | 22852.54 |
| 473 | 0,85 | 0,15 | 0.6894 | 6.4337 | 29606.52 | 20410.33 |
| 498 | 0,90 | 0,10 | 0.5860 | 6.4688 | 29768.01 | 17443.57 |
| 523 | 0,94 | 0,06 | 0.4459 | 6.5699 | 30233.54 | 13480.50 |
| 548 | 0,99 | 0,01 | 0.1967 | 6.8372 | 31463.59 | 6188.09 |
Этилнонаноат
Уравнение Ли-Кесслера.
![]() ;
;
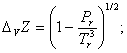 для стандартных условий
для стандартных условий ![]()
![]()
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление возьмем из задания №7 ![]() ацентрический фактор
ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,44 | 1.0000 | 11.4648 | 64244.39 | 64242.61 |
| 323 | 0,48 | 0.9998 | 11.1190 | 62306.90 | 62296.92 |
| 348 | 0,52 | 0.9993 | 10.7771 | 60390.98 | 60350.49 |
| 373 | 0,55 | 0.9978 | 10.4408 | 58506.32 | 58378.39 |
| 398 | 0,59 | 0.9941 | 10.1123 | 56665.86 | 56334.35 |
| 423 | 0,63 | 0.9866 | 9.7948 | 54886.46 | 54153.43 |
| 448 | 0,66 | 0.9732 | 9.4920 | 53189.80 | 51763.12 |
| 473 | 0,70 | 0.9514 | 9.2089 | 51603.34 | 49097.81 |
| 498 | 0,74 | 0.9192 | 8.9516 | 50161.38 | 46109.67 |
| 523 | 0,78 | 0.8745 | 8.7276 | 48906.26 | 42770.33 |
| 548 | 0,81 | 0.8156 | 8.5462 | 47889.74 | 39060.56 |
| 573 | 0,85 | 0.7408 | 8.4185 | 47174.48 | 34945.29 |
| 598 | 0,89 | 0.6475 | 8.3581 | 46835.64 | 30325.72 |
| 623 | 0,92 | 0.5309 | 8.3808 | 46962.70 | 24932.39 |
| 648 | 0,96 | 0.3769 | 8.5054 | 47661.40 | 17964.23 |
Корреляция Риделя.
![]() ;
;
![]()
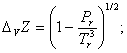 для стандартных условий
для стандартных условий ![]() ,
,
R=8.314, ![]() -возьмем из задания №3.,
-возьмем из задания №3., ![]() -Возьмем из задания №7.,
-Возьмем из задания №7., ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,44 | 1.0000 | 11.4019 | 63892.07 | 63890.62 |
| 323 | 0,48 | 0.9999 | 11.0697 | 62030.77 | 62022.81 |
| 348 | 0,52 | 0.9995 | 10.7414 | 60190.72 | 60159.05 |
| 373 | 0,55 | 0.9983 | 10.4185 | 58381.48 | 58282.90 |
| 398 | 0,59 | 0.9955 | 10.1034 | 56615.80 | 56363.17 |
| 423 | 0,63 | 0.9899 | 9.7990 | 54910.29 | 54356.06 |
| 448 | 0,66 | 0.9798 | 9.5092 | 53286.33 | 52212.59 |
| 473 | 0,70 | 0.9636 | 9.2388 | 51770.97 | 49887.59 |
| 498 | 0,74 | 0.9394 | 8.9938 | 50398.01 | 47344.84 |
| 523 | 0,78 | 0.9054 | 8.7817 | 49209.18 | 44554.10 |
| 548 | 0,81 | 0.8595 | 8.6115 | 48255.50 | 41476.58 |
| 573 | 0,85 | 0.7991 | 8.4943 | 47598.71 | 38033.97 |
| 598 | 0,89 | 0.7196 | 8.4432 | 47312.87 | 34045.76 |
| 623 | 0,92 | 0.6124 | 8.4742 | 47486.18 | 29080.47 |
| 648 | 0,96 | 0.4551 | 8.6056 | 48222.85 | 21945.69 |
Корреляция Амброуза-Уолтона.
![]() ;
;

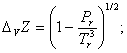 для стандартных условий
для стандартных условий ![]() ;
;
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление![]() возьмем из задания №7
возьмем из задания №7 ![]() ; ацентрический фактор
; ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | τ | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,44 | 0,56 | 1.0000 | 11.6469 | 65265.10 | 65263.59 |
| 323 | 0,48 | 0,52 | 0.9999 | 11.2026 | 62775.22 | 62766.78 |
| 348 | 0,52 | 0,48 | 0.9994 | 10.7833 | 60425.86 | 60392.06 |
| 373 | 0,55 | 0,45 | 0.9982 | 10.3916 | 58230.86 | 58126.22 |
| 398 | 0,59 | 0,41 | 0.9953 | 10.0292 | 56200.20 | 55934.88 |
| 423 | 0,63 | 0,37 | 0.9894 | 9.6975 | 54341.11 | 53765.91 |
| 448 | 0,66 | 0,34 | 0.9791 | 9.3974 | 52659.43 | 51557.10 |
| 473 | 0,70 | 0,30 | 0.9625 | 9.1300 | 51161.07 | 49244.33 |
| 498 | 0,74 | 0,26 | 0.9381 | 8.8967 | 49853.92 | 46766.08 |
| 523 | 0,78 | 0,22 | 0.9038 | 8.6998 | 48750.27 | 44062.01 |
| 548 | 0,81 | 0,19 | 0.8578 | 8.5427 | 47870.43 | 41063.33 |
| 573 | 0,85 | 0,15 | 0.7973 | 8.4318 | 47248.74 | 37671.05 |
| 598 | 0,89 | 0,11 | 0.7180 | 8.3776 | 46945.27 | 33707.95 |
| 623 | 0,92 | 0,08 | 0.6116 | 8.4007 | 47074.55 | 28792.48 |
| 648 | 0,96 | 0,04 | 0.4563 | 8.5493 | 47907.07 | 21861.41 |
орто-Толуидин
Уравнение Ли-Кеслера.
![]() ;
;
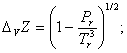 для стандартных условий
для стандартных условий ![]()
![]()
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
приведенное давление возьмем из задания №7 ![]() ацентрический фактор
ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,43 | 0.9999 | 9.8243 | 56685.37 | 56680.93 |
| 323 | 0,47 | 0.9996 | 9.5727 | 55233.81 | 55214.09 |
| 348 | 0,50 | 0.9988 | 9.3237 | 53797.14 | 53730.32 |
| 373 | 0,54 | 0.9965 | 9.0785 | 52382.03 | 52199.21 |
| 398 | 0,57 | 0.9917 | 8.8385 | 50997.40 | 50575.20 |
| 423 | 0,61 | 0.9829 | 8.6058 | 49654.90 | 48803.53 |
| 448 | 0,65 | 0.9682 | 8.3830 | 48369.46 | 46830.40 |
| 473 | 0,68 | 0.9460 | 8.1734 | 47160.03 | 44612.70 |
| 498 | 0,72 | 0.9147 | 7.9811 | 46050.27 | 42123.75 |
| 523 | 0,75 | 0.8732 | 7.8111 | 45069.38 | 39352.75 |
| 548 | 0,79 | 0.8202 | 7.6696 | 44253.07 | 36297.53 |
| 573 | 0,83 | 0.7550 | 7.5642 | 43644.54 | 32950.31 |
| 598 | 0,86 | 0.6761 | 7.5037 | 43295.65 | 29273.91 |
Корреляция Риделя.
![]() ;
;
![]()
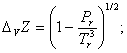 для стандартных условий
для стандартных условий ![]() ,
,
R=8.314, ![]() -возьмем из задания №3.,
-возьмем из задания №3., ![]() -Возьмем из задания №7.,
-Возьмем из задания №7., ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .
.
| Т | Тr | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,43 | 0.9999 | 9.8083 | 56592.86 | 56589.17 |
| 323 | 0,47 | 0.9997 | 9.5638 | 55182.60 | 55166.40 |
| 348 | 0,50 | 0.9990 | 9.3220 | 53787.09 | 53732.81 |
| 373 | 0,54 | 0.9972 | 9.0838 | 52412.99 | 52265.82 |
| 398 | 0,57 | 0.9934 | 8.8509 | 51069.12 | 50731.77 |
| 423 | 0,61 | 0.9864 | 8.6253 | 49767.03 | 49090.68 |
| 448 | 0,65 | 0.9749 | 8.4094 | 48521.56 | 47303.74 |
| 473 | 0,68 | 0.9575 | 8.2066 | 47351.50 | 45340.02 |
| 498 | 0,72 | 0.9330 | 8.0210 | 46280.30 | 43179.35 |
| 523 | 0,75 | 0.9001 | 7.8575 | 45336.96 | 40809.64 |
| 548 | 0,79 | 0.8577 | 7.7223 | 44556.89 | 38217.76 |
| 573 | 0,83 | 0.8042 | 7.6228 | 43982.95 | 35372.64 |
| 598 | 0,86 | 0.7373 | 7.5680 | 43666.59 | 32195.54 |
Корреляция Амброуза-Уолтона.
![]() ;
;

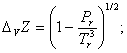 для стандартных условий
для стандартных условий ![]() ;
;
приведенную температуру найдем как ![]() , в интервале от 298К до
, в интервале от 298К до ![]() .приведенное давление
.приведенное давление![]() возьмем из задания №7
возьмем из задания №7 ![]() ; ацентрический фактор
; ацентрический фактор ![]() возьмем из задания №3.
возьмем из задания №3.
| Т | Тr | τ | ΔvZ | Ψ | ΔvH0T | ΔvHT |
| 298 | 0,43 | 0,57 | 0.9999 | 9.9332 | 57313.91 | 57309.90 |
| 323 | 0,47 | 0,53 | 0.9997 | 9.6013 | 55398.51 | 55380.79 |
| 348 | 0,50 | 0,50 | 0.9989 | 9.2896 | 53599.93 | 53540.99 |
| 373 | 0,54 | 0,46 | 0.9970 | 8.9999 | 51928.88 | 51771.26 |
| 398 | 0,57 | 0,43 | 0.9929 | 8.7337 | 50392.60 | 50036.94 |
| 423 | 0,61 | 0,39 | 0.9857 | 8.4916 | 48995.70 | 48293.39 |
| 448 | 0,65 | 0,35 | 0.9739 | 8.2741 | 47741.05 | 46492.63 |
| 473 | 0,68 | 0,32 | 0.9562 | 8.0817 | 46630.75 | 44588.67 |
| 498 | 0,72 | 0,28 | 0.9315 | 7.9147 | 45667.31 | 42539.45 |
| 523 | 0,75 | 0,25 | 0.8986 | 7.7740 | 44855.10 | 40305.05 |
| 548 | 0,79 | 0,21 | 0.8561 | 7.6608 | 44202.31 | 37841.82 |
| 573 | 0,83 | 0,17 | 0.8026 | 7.5779 | 43723.93 | 35091.30 |
| 598 | 0,86 | 0,14 | 0.7356 | 7.5299 | 43446.84 | 31959.08 |
Задание №9
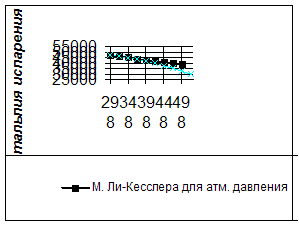
Для первого вещества рекомендованными методами рассчитать вязкость вещества при Т=730К и низком давлении.
Теоретический расчет:
![]()
где ![]() -вязкость при низком давлении; М- молярная масса; Т- температура;
-вязкость при низком давлении; М- молярная масса; Т- температура; ![]() -интеграл столкновений;
-интеграл столкновений; ![]() диаметр.
диаметр.
![]()
где характеристическая температура ![]() где
где ![]() - постоянная Больцмана;
- постоянная Больцмана; ![]() - энергетический параметр; A=1.16145;B=0.14874; C=0.52487; D=077320; E=2.16178; F=2.43787.
- энергетический параметр; A=1.16145;B=0.14874; C=0.52487; D=077320; E=2.16178; F=2.43787.
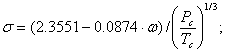 где
где ![]() - ацентрический фактор;
- ацентрический фактор; ![]() и
и ![]() -возьмем из предыдущих заданий.
-возьмем из предыдущих заданий.
![]()
3,4,4-Триметилгептан
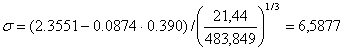 ;
;
![]() ;
;
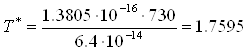
![]()
![]()
Метод Голубева.
Т.к. приведенная температура ![]() то используем формулу:
то используем формулу:
![]()
где 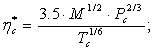 где
где ![]() - молярная масса, критическое давление и критическая температура соответственно.
- молярная масса, критическое давление и критическая температура соответственно.
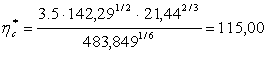
![]() мкП.
мкП.
Метод Тодоса.
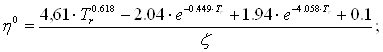
где ![]()
![]() - критическая температура, критическое давление, молярная масса соответственно.
- критическая температура, критическое давление, молярная масса соответственно.
![]()
![]()
Задание №10.
Для первого соединения рассчитать рекомендованными методами вязкость вешества при температуре 730К. и давлении 100атм.
3,4,4-Триметилгептан
Расчет, основанный на понятии остаточной вязкости.
![]()
где ![]() - вязкость плотного газа мкП;
- вязкость плотного газа мкП; ![]() - вязкость при низком давлении мкП;
- вязкость при низком давлении мкП; ![]() - приведенная плотность газа;
- приведенная плотность газа; ![]()
![]()
![]()
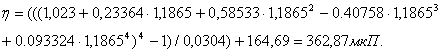
Задание №11
Для первого вещества рекомендованными методами рассчитать теплопроводность вещества при температуре 730К и низком давлении.
Теплопроводность индивидуальных газов при низких давлениях рассчитывается по:
Корреляции Эйкена;
Модифицированной корреляции Эйкена и по корреляции Мисика-Тодоса.
Корреляция Эйкена.
![]()
где ![]() взято из задания №9; М=142,29г/моль молярная масса вещества;
взято из задания №9; М=142,29г/моль молярная масса вещества; ![]() - изобарная теплоемкость; R=1,987.
- изобарная теплоемкость; R=1,987.
![]()
![]() ;
;
![]()
Модифицированная корреляция Эйкена.
![]()
где ![]() взято из задания №9; М=142,29/моль молярная масса вещества;
взято из задания №9; М=142,29/моль молярная масса вещества; ![]() - изобарная теплоемкость.
- изобарная теплоемкость.
![]()
![]() ;
;
![]()
Корреляция Мисика-Тодоса.
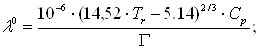
где 
![]() - критическая температура давление и молярная масса соответственно;
- критическая температура давление и молярная масса соответственно; ![]() теплоемкость вещества при стандартных условиях;
теплоемкость вещества при стандартных условиях; ![]() - приведенная температура.
- приведенная температура.
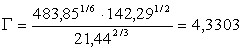
![]()
Задание №12
Для первого соединения рассчитать рекомендованными методами теплопроводность вещества при температуре 730К и давлении 100 атм.
3,4,4-Триметилгептан
![]() , выбираем уравнение:
, выбираем уравнение:
![]()
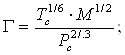

Где ![]() - критическая температура давление объем и молярная масса соответственно.
- критическая температура давление объем и молярная масса соответственно.
![]() ,
,![]() ,
, ![]() .
.
Похожие работы
... Выпишем парциальные вклады для температуры, давления и объема: Группа к-во ΔT ΔP СН2 (цикл) 4 0,04 -0,0112 Сумма 4 0,04 -0,0112 Критическая температура. Критическое давление. ; о-Ксилол, 1,2-диметилбензол Выпишем парциальные вклады для температуры, давления и объема: Группа кол-во ΔT ΔP CН3 2 0,0282 -0,0024 -СН=(цикл) 4 0, ...
... температура. Для пропилизобутаноата Критическое давление. Для пропилизобутаноата ; Критический объем. Ацентрический фактор. Для пропилизобутаноата: 2-метил-2-пентанол. Для 2-метил-2-пентанола выпишем парциальные вклады для температуры, давления и объема: Группа к-во - 3 0,06 0,681 165 -- 2 0,04 0,454 110 1 0 0,21 41 ...
... Задание №5 Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента. Для определения плотности вещества воспользуемся методом прогнозирования плотности индивидуальных веществ с использованием коэффициента сжимаемости. где -плотность вещества; М- молярная масса; V-объем. Для данного вещества найдем коэффициент ...
... . Ацентрический фактор. Поскольку для вещества отсутствуют экспериментальные значения критических параметров, используем параметры, полученные методом Лидерсена. ; 2-Изопропил-5-метилфенол Выпишем парциальные вклады для температуры, давления и объема: Группа к-во CН3 3 0,06 0,681 165 =СН ( ...
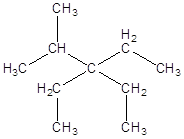
0 комментариев