Навигация
Матричные элементы молекулярного гамильтониана
3. Матричные элементы молекулярного гамильтониана.
Матричные элементы гамильтониана суть
![]() ( 12 )
( 12 )
Они между собою попарно равны, а именно:
-диагональные ![]()
-недиагональные ![]() .
.
4. Энергетические уровни.
Энергия равна ![]() , и получается выражение для двух уровней:
, и получается выражение для двух уровней:
![]() ( 13 )
( 13 )
Цель всех расчётов дать читателю возможность осуществить компьютерно-графическое моделирование основных молекулярных характеристик.
Атомное и двуцентровые слагаемые молекулярного гамильтониана -
матричные элементы гамильтониана
а) диагональный элемент имеет вид суммы трёх слагаемых: ![]()
![]()
![]() . ( 14 )
. ( 14 )
б) недиагональный элемент также распадается на три слагаемых. При этом Hba= Hab:
 . (15 )
. (15 )
![]() . ( 16 )
. ( 16 )
Вначале подойдём ко всем одноэлектронным молекулярным интегралам просто как к параметрам, не раскрывая их. Вычислим их в явном виде чуть далее.
Энергетические уровни и молекулярные интегралы
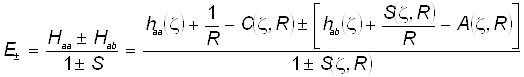
![]()
Выражение для энергии представим в симметричном виде, а именно:
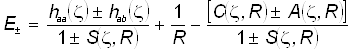 а.е. (17 )
а.е. (17 )
В этой формуле в числителе первой дроби представлены матричные элементы одноцентрового оператора ![]() . По своему виду он совпадает с электронным гамильтонианом водородоподобного атома (иона), но следует помнить, что такой оператор искусственно выделен лишь как одно из удобных слагаемых в молекулярном гамильтониане, и поэтому всё, что с ним связано, выделено просто соображениями математического и классификационного удобства.
. По своему виду он совпадает с электронным гамильтонианом водородоподобного атома (иона), но следует помнить, что такой оператор искусственно выделен лишь как одно из удобных слагаемых в молекулярном гамильтониане, и поэтому всё, что с ним связано, выделено просто соображениями математического и классификационного удобства.
Рассчитанные энергетические уровни МО этой простейшей одноэлектронной молекулы включают лишь те компоненты энергии, которые были учтены в гамильтониане, а именно: кинетическую энергию электрона, движущегося в поле обоих ядер, потенциальную энергию его электростатического (кулоновского) притяжения к обоим ядрам и потенциальную энергию взаимного кулоновского отталкивания ядер. Кинетическая энергия ядер в составленном нами гамильтониане отсутствует, и потому она не включена и в рассчитанные уровни
МО, которые в этом виде не совпадают с полной энергией системы в каждом из состояний. Отличие невелико (всего-навсего на величину энергии взаимных периодических движений ядер - колебаний ядерного остова молекулы), и всё же о нём не следует забывать. Для такого напоминания пригодно и само название. Поэтому полученные энергетические функции,
рассчитанные в приближении фиксированных ядер называют адиабатическими потенциалами. Устойчивым состояниям молекул отвечают лишь такие адиабатические потенциалы, у которых имеются один или несколько минимумов. Они-то и представляют интерес в первую очередь.
Согласно теоретической модели метода МО ЛКАО уровни (адиабатические потенциалы) выражены с помощью нескольких одноэлектронных молекулярных интегралов:
1)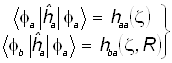
2) ![]() - интеграл перекрывания
- интеграл перекрывания
3) 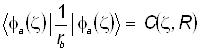 - кулоновский интеграл
- кулоновский интеграл
4) 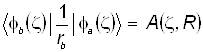 - обменный интеграл (18)
- обменный интеграл (18)
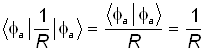 -энергия электростатического отталкивания ядер
-энергия электростатического отталкивания ядер
Нормированные молекулярные орбитали имеют вид:
 . (19 )
. (19 )
![]() (=1)
(=1) ![]()
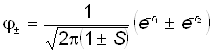 . (20 )
. (20 )
Предварительно введём несколько вспомогательных формул, необходимых
для расчёта числовых значений специальных несобственных интегралов вида:
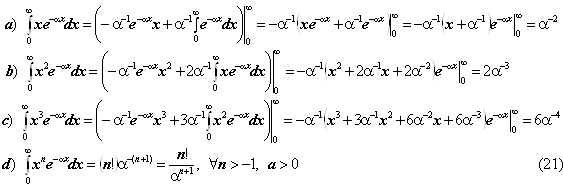
Расчёт энергетические уровни МО
(с варьированием показателя экспоненты базисных водородоподобных АО).
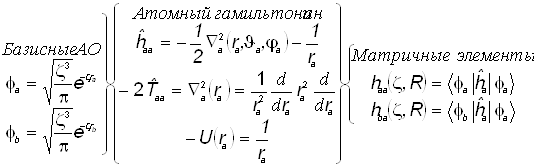 . (22 Напомним, что в шаровых координатах лапласиан имеет вид
. (22 Напомним, что в шаровых координатах лапласиан имеет вид
![]() . ( 23 )
. ( 23 )
Поскольку выбранные нами базисные s-АО не зависят от угловых переменных, то и результат действия на них угловой части лапласиана, составляющей оператор Лежандра, нулевой. Поэтому имеет смысл в выкладках оставить лишь радиальную часть лапласиана, а соответственно, символ частного дифференцирования следует заменить символом полного дифференцирования по единственной оставшейся переменной r.
Вычисление матричных элементов одноцентрового
(атомного) гамильтониана
1) Диагональные матричные элементы haa = hbb
![]() . ( 24 )
. ( 24 )
Нижний индекс в данном пункте расчёта удобно опустить.
Слагаемое 1 (порождено потенциальным слагаемым атомного гамильтониана):
![]() . ( 25 )
. ( 25 )
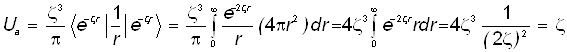 ; ( 26)
; ( 26)
![]() . (27)
. (27)
Слагаемое 2 (порождено кинетическим слагаемым атомного гамильтониана):
Это слагаемое рассчитывается по формуле:
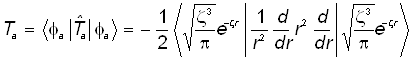 . (28)
. (28)
а) Заменим дифференциальные операции более простыми выражениями. Для этого рассмотрим преобразуем волновую функцию, следуя операторному уравнению![]() :
:
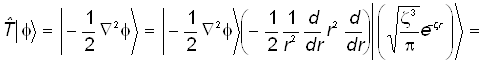
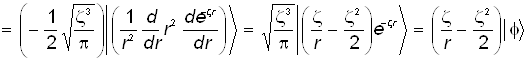 . (29)
. (29)
Из последней цепочки равенств следует координатное выражение атомного оператора кинетической энергии. Опуская в ней промежуточные и оставляя лишь начальное и конечное выражения, приходим к привычной форме операторного уравнения:
 . (30)
. (30)
б) Умножая последнее равенство слева на бра-вектор, получаем искомые кинетические слагаемые и диагонального и недиагонального матричных элементов атомного гамильтониана:
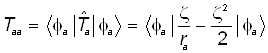 , (31)
, (31)
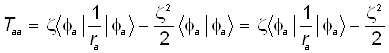 . (32)
. (32)
Учитывая нормировку АО ![]() , а также принимая во внимание равенство
, а также принимая во внимание равенство
![]() , получаем:
, получаем: ![]() . (33)
. (33)
Диагональный матричный элемент одноцентрового гамильтониана получается суммированием потенциального и кинетического слагаемых. Он не зависит от межъядерного расстояния:
![]() . ( 34)
. ( 34)
2) Недиагональные матричные элементы hab = hba
![]() . (35)
. (35)
Здесь уже постоянно встречаются оба индекса, и в отличие от расчётов диагонального матричного элемента их опускать нельзя.
Слагаемое 1 (Порождено потенциальной частью одноцентрового гамильтониана)
Это уже знакомый одноэлектронный резонансный интеграл:
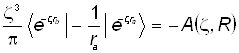 . ( 36 )
. ( 36 )
Для расчёта одноэлектронных двуцентровых интегралов необходимо перейти к двуцентровой эллиптической системе координат.
Слагаемое 2 (Порождено кинетической частью одноцентрового гамильтониана)
а) Используем полученное выше выражение для ![]() и получаем
и получаем

![]()
![]()

![]() (37 )
(37 )
Результат - весь недиагональный матричный элемент атомного гамильтониана:
Суммируя потенциальное и кинетическое слагаемые, получаем недиагональный матричный элемент атомного гамильтониана. Он зависит и от показателя экспоненты, и от межъядерного расстояния:
![]() . (38 )
. (38 )
Для расчёта интегралы S, C, A следует перевести в двуцентровую систему координат.
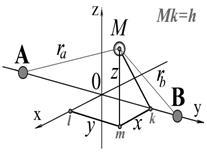
Двуцентровые эллиптические (сфероидальные)координаты
Для расчёта необходимы переменные, позволяющие вычислить молекулярные интегралы. В данной задаче такие естественные пространственные переменные возникают в двуцентровой системе координат. В ней всякий эллипсоид вращения характеризуется условием![]() , и всякий гиперболоид вращения - условием
, и всякий гиперболоид вращения - условием ![]() . Центрированные в одних и тех же полюсах системы эллипсоидов и гиперболоидов образуют совокупности взаимно перпендикулярных поверхностей. Это означает, что в любой точке пространства касательные плоскости к пересекающимся эллипсоиду и гиперболоиду взаимно перпендикулярны.
. Центрированные в одних и тех же полюсах системы эллипсоидов и гиперболоидов образуют совокупности взаимно перпендикулярных поверхностей. Это означает, что в любой точке пространства касательные плоскости к пересекающимся эллипсоиду и гиперболоиду взаимно перпендикулярны.
В декартовых координатах пространство разбито на элементы системой взаимно ортогональных плоскостей, а в эллиптической - системами концентрических эллипсоидов, гиперболоидов и пучком плоскостей, пересекающихся на оси вращения.
Всякая точка в декартовых координатах вписана в элемент объёма, ограниченный шестью плоскостями, по две вдоль каждой из трёх взаимно перпендикулярных осей координат.
В эллиптических координатах точка ограничена: “сверху и снизу” - двумя эллипсоидами вращения, “с торцов” - двумя гиперболоидами вращения, “по бокам” - двумя плоскостями, пересекающимися на оси вращения. Ядра молекулы расположены в полюсах координатных поверхностей второго порядка. В каждой вершине пространственного элемента плоскости, касательные к координатным поверхностям, взаимно перпендикулярны, но элемент пространства изначально не является прямоугольным параллелепипедом, и потому его элементарный объём рассчитывается не просто как произведение дифференциалов координат. Формула для его вычисления окажется сложнее и должна учитывать искривление координатных поверхностей.
Вычисление элемента объёма в эллиптических переменных
| |||
| |||
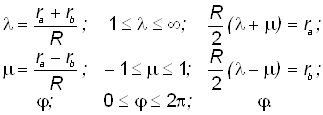
0 комментариев