На основе данных таблицы1 строим диаграмму рассеивания

2. На основе данных таблицы1 строим диаграмму рассеивания.

Визуально можно предположить, что между данными существует линейная зависимость, то есть их можно аппроксимировать линией.

Y = b₀ + b₁X

3. Найдем параметры b₀ и b₁.

Опишем полученный результат:

в первой строке находятся оценки параметров регрессии b₁, b₀;

во второй строке находятся средние квадратичные отклонения s_b1, s_b0.

в третьей строке в первой ячейке находится коэффициент детерминации R², а во второй ячейке оценка среднего квадратичного отклонения показателя s_е.

в четвертой строке в первой ячейке находится расчетное значение F - статистики, во второй ячейке находится k - число степеней свободы;

в пятой строке в первой ячейке находится сумма квадратов отклонений расчетных значений показателя от его среднего значения, а во второй ячейке - сумма квадратов остатков.

Полученные результаты заносим в таблицу 2.

Таблица 2.

Результаты расчетов
1,958977	5,277335
0,10027	0,671183
0,967063	0,836194
381,6981	13
266,8909	9,089857

По данным таблицы 2 можем записать модель:

Y = 5,277335 + 1,958977Х

Коэффициент детерминации R² = 0,967063 - близок к 1, следовательно, модель адекватна.

4. Найдем прогноз в заданной точке X_p = 10,1. Для этого подставим X_pв модель. Получим

Y_p = 5,277335 + 1,958977 * 10,1 = 25,063.

Все полученные результаты запишем в таблицу 3.

Таблица 3.

X	Y
3.11	10.65
3.15	11.87
3.85	12.69
4.84	13.40
4.62	15.12
4.87	16.03
6.09	16.29
7.06	18.07
6.23	18.40
6.83	19.53
8.01	20.48
8.26	21.72
9.37	23.17
9.02	23.57
9.76	24.41
10,1	25,063

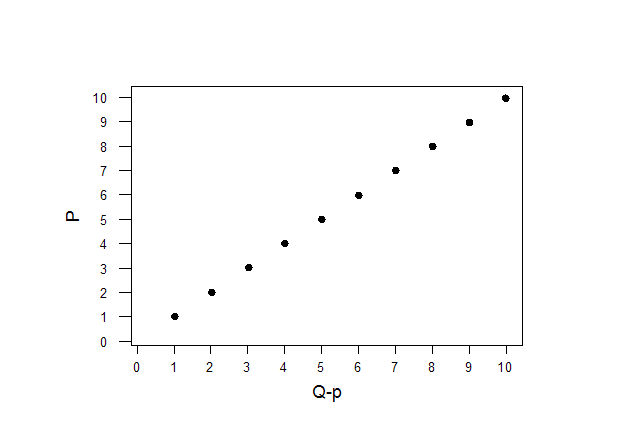
5. Диаграмма примет вид:

6. Вычислим коэффициент корреляции r. В результате расчета получим коэффициент корреляции r = 0,9834.

r =  = √0,967063 = 0.9834

 

Задание № 2.

По заданным статистическим данным с помощью пакета "Excel":

построить диаграмму рассеивания и подтвердить гипотезу о криволинейной связи между Х и Y;

произвести линеаризацию;

определить параметры a и b;

сделать прогноз в указанной точке;

Решение:

Набираем исходные данные в таблицу 1:

Таблица 1.

X	Y
1,03	0,44
1,63	0,33
2,16	0,25
2,71	0, 20
3,26	0,16
3,77	0,12
4,35	0,10
4,91	0,07
5,50	0,05
6,01	0,04

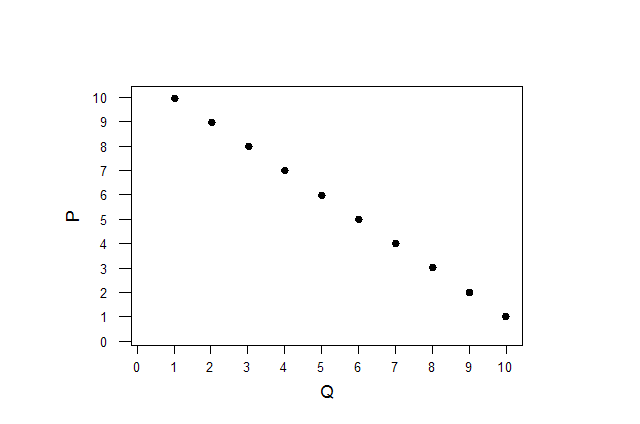
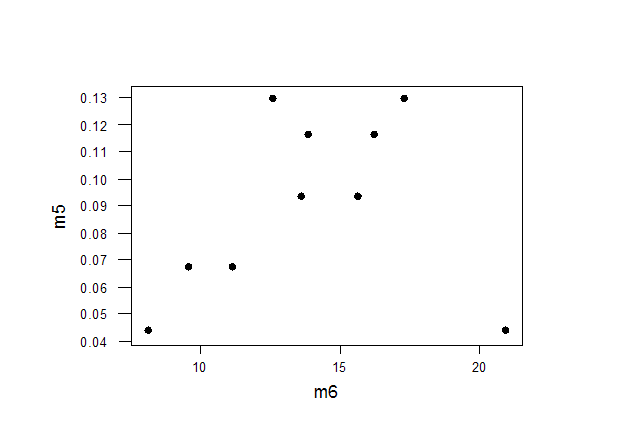
На основе данных таблицы 1 строим диаграмму рассеивания.

	beax

Визуально можно предположить, что зависимость не линейная. Исходная модель имеет вид Y = be^ax. Делаем линеаризующую подстановку: V = Y, U = lnX.

Полученные данные заносим в таблицу 2.

Таблица 2.

X	Y	V	U
1,03	0,44	0,44	0.02956
1,63	0,33	0,33	0.48858
2,16	0,25	0,25	0.77011
2,71	0, 20	0, 20	0.99695
3,26	0,16	0,16	1.18173
3,77	0,12	0,12	1.32708
4,35	0,10	0,10	1.47018
4,91	0,07	0,07	1.59127
5,50	0,05	0,05	1.70475
6,01	0,04	0,04	1.79342

Строим корреляционное поле:

Визуально можно предположить, что между данными существует линейная зависимость, то есть их можно аппроксимировать линией

Y = b₁X + b₀

Диаграмма примет вид:

3. Найдем параметры b₀ и b₁.

Полученные результаты заносим в таблицу 3.

Таблица 3.

Результаты расчета
-0,2297	0,436791
0,005542	0,006967
0,995364	0,009454
1717,627	8
0,153525	0,000715

Параметры модели b₀ = 0,436791, b₁ = - 0,2297. Коэффициент детерминации R² = 0,995364 - близок к 1, следовательно, модель адекватна.

Находим параметры исходной нелинейной модели:

а = е^b1 = e^-0,2297 = 0,79477

b = e^b0 = e^0,436791 = 1,54773

Исходная нелинейная модель примет вид: Y = 1,54773e^0,79477X

5. Вычислим прогнозируемое Y_p в то X_p = 6,5:

Y_p = 1,54773e ^0,79477*6,5 = 271,18

 

Задание № 3

По заданным статистическим данным с помощью пакета "Excel":

построить корреляционную матрицу;

по корреляционной матрице проверить факторы X₁, X₂, X₃ на мультиколинеарность, и, если она есть, устранить ее, исключив один из факторов;

проверить гипотезу о наличии линейной связи между показателем Y и оставшимися факторами;

определить параметры линейной связи;

вычислить коэффициент детерминации;

сделать прогноз в указанной точке.

Решение:

Набираем исходные данные в таблицу 1:

Таблица 1.

X1	X2	X3	Y
2,61	10,35	6,61	7,72
4,89	11,78	7,94	10,77
6,24	14,09	8,62	11,86
9,01	14,64	8,83	13,73
10,79	15,17	10,68	17,04
13,53	17,42	10,66	18,8
16,32	19,24	11,78	21,28
18,6	20,6	13,78	23,7
21,48	22,04	13,74	27,63
23,02	22,69	14,56	27,45
25,17	22,65	14,09	29,71
26,4	24,83	16,66	32,8
27,62	24,82	15,12	31,81
30, 19	25,17	15,42	25,22
32,25	26,22	15,77	37,26
33,76	27,72	17,4	39,2
35,97	29,15	17,77

2. По исходным данным строим корреляционную матрицу (таблица 2):

Таблица 2.

	X1	X2	X3	Y
X1	1	0,9921671	0,9741853	0,9656738
X2	0,9921671	1	0,9864174	0,9700431
X3	0,9741853	0,9864174	1	0,96548
Y	0,9656738	0,9700431	0,96548	1

Визуально можно предположить, что между данными X₂ и X₃ и X₁ и X₃ есть зависимость, значит, фактор X₃ исключаем из модели, так как между ним и Y связь меньше, чем между Y и X₂ (0,96548 < 0,9700431). Модель будет иметь вид:

Y = b₀ + b₁X₁ + b₂X₂;

3. Строим график зависимости между X₁, X₂ и Y: визуально можно предположить, что зависимость между X₁, X₂ и Y линейная, коэффициент детерминации R² = 0,9416518 - близок к 1, следовательно, модель адекватна.

4. Найдем параметры b₀, b₁ и b₂. Полученные результаты заносим в таблицу 3:

Таблица 3.

Результаты расчета
1,344552	0, 1954415	-7,0318824
0,9429349	0,5065553	9,4389862
0,9416518	2,4854573	---
104,90023	13	---
1296,0419	80,307473	---

 

 5. По данным таблицы можем записать модель:

Y = - 7,0318824 + 0, 1954415X₁ + 1,344552X₂;

Коэффициент детерминации R² = 0,9416518 - близок к 1, следовательно, модель адекватна.

6. Найдем прогноз в заданной точке. Для этого достаточно подставить X_p в модель.

Y_p = - 7,0318824 + 0, 1954415 * 35,97 + 1,344552 * 29,15 = 39, 19

 

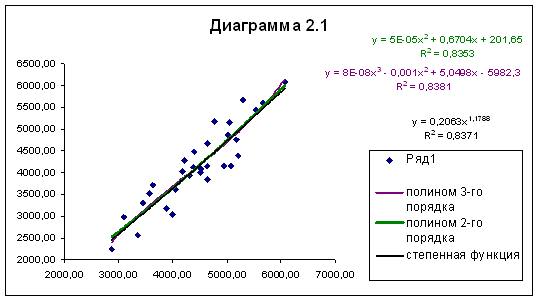
Задание №4.

Предположим, что между показателем Y - объем выпущенной продукции и факторами X₁ - трудовые затраты, X₂ - объем основных фондов, существует зависимость типа

Y = AX × X

(производная функция Кобба-Дугласа). По приведенным статистическим данным с помощью пакета "Excel":

определить коэффициенты А, б₁, б ₂;

вычислить прогноз в указанной точке;

определить коэффициент эластичности по каждому из факторов в точке прогноза.

Решение:

1. Набираем исходные данные в таблицу 1:

Таблица 1.

X1	X2	Y
54,2	33,6	75,4
56,8	39,1	85,4
59,7	40,4	88,5
61,4	42,9	92,7
63,5	44	95,2
64,7	46,8	99,5
64,8	51,9	106,2
67,4	56,3	113,2
69	56,6	114,5
70,7	58,7	118,1
71,3	59,6	118,7
73,7	62,4	123
75,9	63,9	127,4
77,5	67,2	?

Так как модель не линейная, перейдем к линейной с помощью замены:

V = lnY, U₁ = lnX₁, U₂ = lnX₂, b₀ = lnA, b₁ = б₁

получим линейную модель:

V = b₀ + b₁U₁ + b₂U₂

Полученные результаты заносим в таблицу 2.

Таблица 2.

X1	X2	Y	V	U1	U2
54,2	33,6	75,4	4,3228	3,9927	3,5145
56,8	39,1	85,4	4,4473	4,0395	3,6661
59,7	40,4	88,5	4,4830	4,0893	3,6988
61,4	42,9	92,7	4,5294	4,1174	3,7589
63,5	44	95,2	4,5560	4,1510	3,7842
64,7	46,8	99,5	4,6002	4,1698	3,8459
64,8	51,9	106,2	4,6653	4,1713	3,9493
67,4	56,3	113,2	4,7292	4,2106	4,0307
69	56,6	114,5	4,74057	4,2341	4,0360
70,7	58,7	118,1	4,7715	4,2584	4,0724
71,3	59,6	118,7	4,7766	4,2669	4,0877
73,7	62,4	123	4,8122	4,3000	4,1336
75,9	63,9	127,4	4,8473	4,3294	4,1573
77,5	67,2			4,3503	4, 2077

2. Найдем параметры b₀, b₁ и b₂. Полученные результаты заносим в таблицу 3:

Таблица 3.

Результаты расчета
1,296429	0,5234561	4,655595
0,09192	0,1394437	4,694014
0,998782	0,6193063	---
4101,677	10	---
3146,317	3,8354032	---

3. По данным таблицы можем записать модель:

V = 4,6556 + 0,5235U₁ + 1,2964U₂

4. Найдем параметры исходной модели:

А = e^bo = e^4.655595 = 105.1723; a₁ = b₁ = 0,5234561; a₂ = b₂ = 1,296429.

Исходная модель имеет вид:

Y = 105.1723 * X₁^0.5235 * X₂^1.2964

5. Найдем прогноз в заданной точке:

Y = 105.1723 * 77.5^0.5235 * 67.2^1.2964 = 239856.97;

Вычислим коэффициент эластичности, который показывает, на сколько% увеличится (если Е_х > 0) или уменьшится (если Е_х < 0) показатель Y, если фактор X изменится на 1%.

E_X1 = (X₁ * ∂y) / (y * ∂x₁) = (X_1/ (105.1723 * X₁^0.5235 * X₂^1.2964)) * ( (∂ (105.1723 * X₁^0.5235 * X₂^1.2964)) / ∂x₁) = (X_1/ (105.1723 * X₁^0.5235 * X₂^1.2964)) * (105.1723 * X₂^1.2964 * (∂ (X₁^0.5235)) / ∂x₁) = (X_1/X₁^0.5) * 0.5X₁^-0.5 = 0.5X₁^1-0.5-0.5 = 0.5X₁⁰= 0.5

Вывод

Для модели Кобба-Дугласа коэффициент эластичности - это показатели степени a₁ и a₂, при чем a₁ = 0.5235 - коэффициент эластичности по трудозатратам, а a₂ = 1.2964 - коэффициент эластичности по объему основных фондов.

Литература

1.  Лук`яненко І.Г., Краснікова Л.І. Економетрика. Підручник. - К. Товариство “Знання”. - 1998. - 494 с.

2.  Грубер Й. Эконометрия: учебное пособие для студентов экономических специальностей. - К. 1996. - 400 с.

3.  Методические указания и контрольные задания по дисциплине "Эконометрия" для студентов экономического направления заочного факультета. / Сост. В.Н. Черномаз, Т.В. Шевцова, - Харьков: 2006 г. - 32 с.

4.  Конспект лекций по курсу "Эконометрия"