Навигация
Оцінювання якості прогнозів
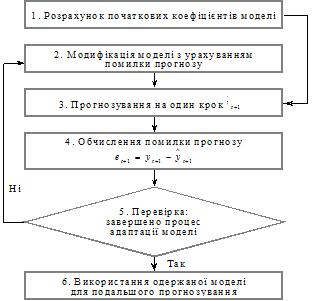
5. Оцінювання якості прогнозів
Забезпечення адекватності регресійної моделіАдекватність регресійної моделі означає здатність її правильно описати реальну структуру взаємозв'язків між ознаками ![]() та y. Методологічною основою вирішення проблеми адекватності є теоретичний, змістовний аналіз матеріальної природи процесу (явища) та обґрунтування типу й структури моделі, яка описує механізм його формування. Практично з метою забезпечення адекватності моделі змістовний аналіз поєднується з формальними процедурами перевірки гіпотез щодо дотримання логіко-статистичних умов використання МНК.
та y. Методологічною основою вирішення проблеми адекватності є теоретичний, змістовний аналіз матеріальної природи процесу (явища) та обґрунтування типу й структури моделі, яка описує механізм його формування. Практично з метою забезпечення адекватності моделі змістовний аналіз поєднується з формальними процедурами перевірки гіпотез щодо дотримання логіко-статистичних умов використання МНК.
Мірою адекватності моделі слугують відхилення фактичних значень від теоретичних ![]() . На величину цих відхилень впливає весь комплекс умов, зокрема:
. На величину цих відхилень впливає весь комплекс умов, зокрема:
- обсяг та однорідність сукупності;
- незалежність спостережень;
- інформативність включених у модель факторів;
- стабільність не включених у модель факторів;
- тип моделі.
Репрезентативність оцінок регресійного аналізу прямо пропорційна обсягу та однорідності сукупності. Саме недостатній обсяг сукупності та її неоднорідність вважаються найвагомішими чинниками неадекватності моделей. Тому при формуванні ознакової множини моделі слід враховувати співвідношення між обсягом вибірки і кількістю включених у модель факторів (воно має бути приблизно 8:1).
Оцінювання однорідності сукупності здійснюється на етапі розвідувального аналізу даних. Так, наявність аномальних значень, які не узгоджуються з розподілом основної маси даних, може бути наслідком помилок спостереження або результатом незвичайної комбінації причин і умов, у яких функціонує одиниця сукупності. Ідентифікація таких спостережень дає можливість Усунути помилки, а якщо це неможливо, то вилучити аномальний об'єкт з подальшого аналізу. Якщо сукупність розшарована на групи (кластери), то в моделі можна врахувати таку неоднорідність.
Інформативність включених у модель факторних ознак залежить як від соціально-економічного змісту, так і від шкали вимірювання ознаки. Якщо ознака за змістом не інформативна, то ніякий спосіб моделювання не забезпечить належних результатів. Так само результати аналізу будуть суттєво різнитися залежно від того, якою шкалою представлено одну й ту саму ознаку (метричною, ранговою чи номінальною).
Ті властивості, що безпосередньо не вимірюються або не мають єдиного вимірника, включаються в модель у вигляді інтегральних оцінок. Наприклад, погодні умови характеризуються середньодобовою температурою повітря, кількістю опадів, тривалістю сонячного світла, хмарністю і т. ін. Усі ці характеристики агрегуються в індексі погодних умов.
Важливою умовою регресійного аналізу є відсутність мультиколінеарності, яка веде до зсунення оцінок параметрів моделі та унеможливлює коректну інтерпретацію результатів. Два фактори вважаються колінеарними, якщо коефіцієнт кореляції між ними перевищує сукупний коефіцієнт кореляції, тобто ![]() . Найпростіший спосіб усунення мультиколінеарності — виключити одну із корельованих ознак із моделі або замінити її іншою. Часом колінеарні фактори агрегуються в одну узагальнюючу оцінку.
. Найпростіший спосіб усунення мультиколінеарності — виключити одну із корельованих ознак із моделі або замінити її іншою. Часом колінеарні фактори агрегуються в одну узагальнюючу оцінку.
Стабільність не включених у модель факторів означає, що вплив їх на варіацію у незначний і врівноважується, він однаковий в усіх частинах сукупності. Математичною основою дотримання цих передумов МНК слугує імовірнісний розподіл залишків ![]() . Передбачається, що:
. Передбачається, що:
- для кожного спостереження залишок ![]() — випадкова величина, яка має нормальний розподіл. Умова нормальності необхідна для визначення довірчих меж коефіцієнтів регресії і для перевірки гіпотез щодо їх істотності;
— випадкова величина, яка має нормальний розподіл. Умова нормальності необхідна для визначення довірчих меж коефіцієнтів регресії і для перевірки гіпотез щодо їх істотності;
- математичне сподівання залишків М(е) = 0;
- дисперсія залишків однакова в усіх частинах сукупності: ![]() . Ця умова пов'язана з однорідністю сукупності;
. Ця умова пов'язана з однорідністю сукупності;
- залишки незалежні, тобто відсутня серійна кореляція чи автокореляція даних.
Використовуючи параметри моделі, можна також оцінити потенційно можливі рівні показника-функції для кожної одиниці Окупності, визначити резерви збільшення (зменшення) показника у за рахунок факторів, які піддаються регулюванню (суб'єктивних факторів). У нашому прикладі — це збільшення виходу цукру з 1 т сировини за рахунок зменшення витрат при зберіганні цукрового буряка і в процесі його переробки. Така оцінка, природно, орієнтована на кращі досягнення в галузі. Ефект регулювання і-го фактора на ![]() -му об'єкті визначається за формулою
-му об'єкті визначається за формулою
![]() ,
,
де ![]() — база порівняння,
— база порівняння, ![]() — коефіцієнт регресії і-го фактора.
— коефіцієнт регресії і-го фактора.
Застосовуючи цю методику, визначимо резерв збільшення виходу цукру з 1 т сировини для ![]() -го заводу (табл. 5.1).
-го заводу (табл. 5.1).
Таблиця 5.1
| Фактор | Рівень втрат, % | Відхилення | Коефіцієнт регресії | Ефект регулювання фактора | |
| фактичний | мінімальний | ||||
|
| 1,06 | 0,90 | 0,16 | -10,084 | -1,613 |
|
| 2,68 | 2,0 | 0,68 | -1,729 | -1,175 |
| Разом | X | X | X | X | -2,788 |
Якщо мінімальні втрати цукрового буряка при переробці — 2,0%, а на ![]() -му заводі — 2,68%, то ефект доведення втрат до мінімального рівня становить (2,68-2,0)(-1,729) = -1,175. Зменшення втрат при зберіганні цукрового буряка дає ефект (1,06--0,90)(-10,084) = -1,613. Отже, сумарний ефект за рахунок обох факторів -2,788, а потенційно можливий вихід цукру з 1 т сировини за незмінності цукристості буряка, яка є зовнішнім, об'єктивним фактором, становить 11,91 кг. Відношення фактичного рівня до потенційно можливого характеризує ступінь використання об'єктивних можливостей. У розглянутому прикладі це відношення становить 9,13 : 11,91 =0,777, тобто ефективність використання сировини на заводі нижча за потенційно можливу на 23,3%. При визначенні резервів збільшення (зменшення) показника функції за рахунок регулювання суб'єктивних факторів базою порівняння може бути середня величина, норматив, стандарт тощо.
-му заводі — 2,68%, то ефект доведення втрат до мінімального рівня становить (2,68-2,0)(-1,729) = -1,175. Зменшення втрат при зберіганні цукрового буряка дає ефект (1,06--0,90)(-10,084) = -1,613. Отже, сумарний ефект за рахунок обох факторів -2,788, а потенційно можливий вихід цукру з 1 т сировини за незмінності цукристості буряка, яка є зовнішнім, об'єктивним фактором, становить 11,91 кг. Відношення фактичного рівня до потенційно можливого характеризує ступінь використання об'єктивних можливостей. У розглянутому прикладі це відношення становить 9,13 : 11,91 =0,777, тобто ефективність використання сировини на заводі нижча за потенційно можливу на 23,3%. При визначенні резервів збільшення (зменшення) показника функції за рахунок регулювання суб'єктивних факторів базою порівняння може бути середня величина, норматив, стандарт тощо.
Функція нормального розподілу 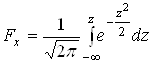 .
.
Додаток 1
| z | 00 | 11 | 22 | 23 | 44 | 55 | 66 | 77 | 88 | 99 |
| 00,0 | 500 | 504 | 508 | 512 | 516 | 520 | 524 | 528 | 532 | 536 |
| 00,1 | 540 | 544 | 548 | 552 | 556 | 560 | 564 | 567 | 571 | 575 |
| 00,2 | 580 | 583 | 587 | 591 | 595 | 599 | 603 | 606 | 610 | 614 |
| 00,3 | 618 | 622 | 626 | 629 | 633 | 637 | 641 | 644 | 648 | 652 |
| 00,4 | 655 | 659 | 663 | 666 | 670 | 674 | 677 | 681 | 684 | 688 |
| 00,5 | 691 | 695 | 698 | 702 | 705 | 709 | 712 | 716 | 719 | 722 |
| 00,6 | 726 | 729 | 732 | 736 | 739 | 742 | 745 | 749 | 752 | 755 |
| 00,7 | 758 | 761 | 764 | 767 | 770 | 773 | 776 | 779 | 782 | 785 |
| 00,8 | 788 | 791 | 794 | 797 | 800 | 802 | 805 | 808 | 811 | 813 |
| 00,9 | 816 | 819 | 821 | 824 | 826 | 829 | 831 | 834 | 836 | 839 |
| 11,0 | 841 | 844 | 846 | 849 | 851 | 853 | 855 | 858 | 860 | 862 |
| 11,1 | 864 | 867 | 869 | 871 | 873 | 875 | 877 | 879 | 881 | 883 |
| 11,2 | 885 | 887 | 889 | 891 | 893 | 894 | 896 | 898 | 900 | 901 |
| 11,3 | 903 | 905 | 907 | 908 | 910 | 911 | 913 | 915 | 916 | 918 |
| 11,4 | 919 | 921 | 922 | 924 | 925 | 926 | 928 | 929 | 931 | 932 |
| 11,5 | 933 | 934 | 936 | 937 | 938 | 939 | 941 | 942 | 943 | 944 |
| 11,6 | 945 | 946 | 947 | 948 | 950 | 951 | 952 | 953 | 954 | 954 |
| 11,7 | 955 | 956 | 957 | 958 | 959 | 960 | 961 | 962 | 962 | 963 |
| 11,8 | 964 | 965 | 966 | 966 | 967 | 968 | 969 | 969 | 970 | 971 |
| 11,9 | 971 | 972 | 973 | 973 | 974 | 974 | 975 | 976 | 976 | 977 |
| 22,0 | 977 | 978 | 978 | 979 | 979 | 980 | 980 | 981 | 981 | 982 |
| 22,1 | 982 | 983 | 983 | 983 | 984 | 984 | 985 | 985 | 985 | 986 |
| 22,2 | 986 | 986 | 987 | 987 | 987 | 988 | 988 | 988 | 989 | 989 |
| 22,3 | 989 | 990 | 990 | 990 | 990 | 991 | 991 | 991 | 991 | 992 |
| 22,4 | 992 | 992 | 992 | 992 | 993 | 993 | 993 | 993 | 993 | 994 |
| 22,5 | 994 | 994 | 994 | 994 | 994 | 995 | 995 | 995 | 995 | 995 |
| 22,6 | 995 | 995 | 996 | 996 | 996 | 996 | 996 | 996 | 996 | 996 |
| 22,8 | 997 | 998 | 998 | 998 | 998 | 998 | 998 | 998 | 998 | 998 |
| 22,9 | 998 | 998 | 998 | 998 | 998 | 998 | 998 | 999 | 999 | 999 |
Критичні значення ![]()
Додаток 2
| /с | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| <х =0,10 | 2,71 | 4,61 | 6,25 | 7,78 | 9,24 | 10,64 | 12,02 | 13,36 | 14,68 | 15,99 | 17,28 |
| а =0,05 | 3,84 | 5,99 | 7,81 | 9,49 | 11,07 | 12,59 | 14,07 | 15,51 | 16,92 | 18,31 | 19,67 |
Квантилі t-розподілу Стьюдента t1-0,05 (k): | t | 1 — двосторонній критерій; t— односторонній критерій
Додаток 3
| Іс | І'І | І | £ | І'І | І |
| 5 | 2,57 | 3,04 | 18 | 2,10 | 2,17 |
| 6 | 2,45 | 2,78 | 20 | 2,09 | 2,15 |
| 7 | 2,37 | 2,62 | 25 | 2,06 | 2,11 |
| 8 | 2,31 | 2,51 | 30 | 2,05 | 2,08 |
| 9 | 2,26 | 2,43 | 40 | 2,02 | 2,05 |
| 10 | 2,23 | 2,37 | 50 | 2,01 | 2,03 |
| 11 | 2,20 | 2,33 | 60 | 2,00 | 2,02 |
| 12 | 2,18 | 2,29 | 100 | 1,98 | 1,99 |
| 14 | 2,15 | 2,24 | ¥ | 1,96 | 1,96 |
| 16 | 2,12 | 2,20 | |||
Значення Z* для оцінювання довірчих меж прогнозу (лінійний тренд)
Додаток 4
| n | V | n | v | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 5 | 1,366 | 1,524 | 1,702 | 10 | 1,211 | 1,270 | 1,335 |
| 7 | 1,309 | 1,427 | 1,558 | 11 | 1,191 | 1,239 | 1,293 |
| 8 | 1,267 | 1,358 | 1,459 | 12 | 1,174 | 1,215 | 1,260 |
| 9 | 1,236 | 1,308 | 1,389 | ||||
Критичні значення циклічного коефіцієнта автокореляції (а = 0,05)
Додаток 5
| n | Додатні значення | Від'ємні значення | n | Додатні значення | Від'ємні значення |
| 5 | 0,253 | -0,753 | 20 | 0,299 | -0,399 |
| 6 | 0,345 | -0,708 | 25 | 0,276 | -0,356 |
| 7 | 0,370 | -0,674 | ЗО | 0,257 | -0,356 |
| 8 | 0,371 | -0,625 | 35 | 0,242 | -0,300 |
| 9 | 0,366 | -0,593 | 40 | 0,229 | -0,279 |
| 10 | 0,360 | -0,564 | 50 | 0,208 | -0,248 |
| 11 | 0,353 | -0,539 | 60 | 0,191 | -0,225 |
| 12 | 0,348 | -0,516 | 70 | 0,178 | -0,207 |
| 13 | 0,341 | -0,497 | 80 | 0,170 | -0,195 |
| 14 | 0,335 | -0,479 | 90 | 0,161 | -0,184 |
| 15 | 0,328 | -0,462 | 100 | 0,154 | -0,174 |
Квантилі F-розподілу (a = 0,05)
Додаток 6
| k2 | k1 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | 4,74 | |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,64 | |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,59 | 3,50 | 3,44 | 3,39 | 3,35 | |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,14 | |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,98 | |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,85 | |
| 12 | 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | 2,75 | |
| 13 | 4,67 | 3,81 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | 2,67 | |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | 2,60 | |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | 2,54 | |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 | 2,46 | 2,41 | |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,39 | 2,35 | |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,46 | 2,40 | 2,34 | 2,30 | |
| 24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2.51 | 2,42 | 2,36 | 2,30 | 2,25 | |
| 26 | 4,23 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 | 2,27 | 2,22 | |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,45 | 2,36 | 2,29 | 2,24 | 2,19 | |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 2,21 | 2,16 | |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | 2,08 | |
| 60 | 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | 1,99 | |
| 120 | 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,09 | 2,02 | 1,96 | 1,91 | |
| ¥ | 3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 2,01 | 1,94 | 1,88 | 1,83 | |
Критичні значення коефіцієнта детермінації R2 кореляційного відношення h2 для рівня істотності α = 0,05
Додаток 7
| k2/k1 | 1 | 2 | 3 | 4 | 5 |
| 5 | 0,569 | 699 | 764 | 806 | 835 |
| 6 | 500 | 632 | 704 | 751 | 785 |
| 7 | 444 | 575 | 651 | 702 | 739 |
| 8 | 399 | 527 | 604 | 657 | 697 |
| 9 | 362 | 488 | 563 | 618 | 659 |
| 10 | 332 | 451 | 527 | 582 | 624 |
| 12 | 283 | 394 | 466 | 521 | 564 |
| 14 | 247 | 348 | 417 | 471 | 514 |
| 16 | 219 | 312 | 378 | 429 | 477 |
| 18 | 197 | 283 | 345 | 394 | 435 |
| 20 | 179 | 259 | 318 | 364 | 404 |
| 24 | 151 | 221 | 273 | 316 | 353 |
| 28 | 130 | 193 | 240 | 279 | 314 |
| 32 | 115 | 171 | 214 | 250 | 282 |
| 36 | 102 | 153 | 192 | 226 | 256 |
| 40 | 093 | 139 | 176 | 207 | 234 |
| 50 | 075 | 113 | 143 | 170 | 194 |
| 60 | 063 | 095 | 121 | 144 | 165 |
| 80 | 047 | 072 | 093 | 110 | 127 |
| 100 | 038 | 058 | 075 | 090 | 103 |
| 120 | 032 | 049 | 063 | 075 | 087 |
| 200 | 019 | 030 | 038 | 046 | 053 |
Похожие работы
... тим при інших рівних умовах, є можливість з більшою впевненістю досягти бажаних результатів. Однак є обставини, які не відповідають наведеному критерію [7, 29]. Основними проблемами прогнозування в прийнятті управлінських рішень є: 1. Достовірність прогнозу може бути оцінена тільки після завершення події, тобто після реалізації управлінського рішення. 2. Критерій оцінки якості ...
... і пільги, збільшують державні інвестиції, що дає змогу зменшити глибину та тривалість імовірного спаду виробництва, збільшити можливість інвестицій та зростання зайнятості. Державне регулювання економіки у сфері галузевої та територіальної структури забезпечують за допомогою фінансових стимулів та державних капіталовкладень, які гарантують привілейовані умови для розвитку окремих галузей та рег ...
... , а й економічно вигідним. Доведемо економічну ефективність впровадження автоматизованої системи для шахти "Добропільська". Інформаційна система, що розроблена для підвищення ефективності підвищення економічних показників роботи шахти "Добропільська", а саме модель максимізації прибутку дала результати, які говорять про те що впровадження інформаційної системи автоматизації є доцільним. Обидві ...
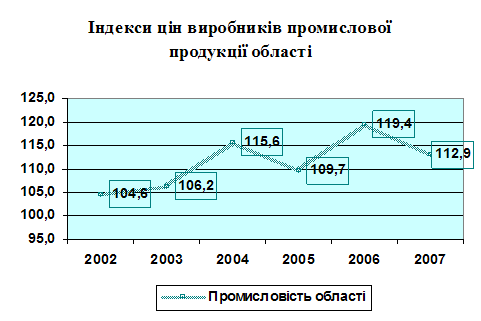
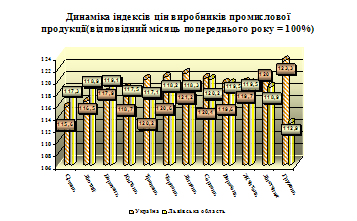
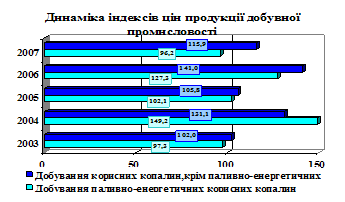
... ікативна модель дає неточні результати. У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1]. РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ 3.1 Статистичний аналіз цін виробників промислової продукції у Львівській області У Львівській області індекс цін виробників промислової продукції у 2007 році ...

0 комментариев