Навигация
Чтобы определить среднегодовую стоимость основных
1. Чтобы определить среднегодовую стоимость основных
производственных фондов в расчете на одно предприятие, необходимо применить формулу средней арифметической простой величины:
![]()
![]()
Ответ: 42 млн. руб.
2. Построим статистический ряд распределения предприятий по
среднегодовой стоимости основных производственных фондов, образовав четыре группы предприятий с равными интервалами:
Сначала найдем интервал группировки:
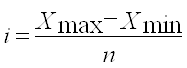
, где
![]() - максимальное значение признаков совокупности;
- максимальное значение признаков совокупности;
![]() - минимальное значение признаков совокупности;
- минимальное значение признаков совокупности;
![]() - число групп.
- число групп.
![]() = 60;
= 60;
![]() = 20;
= 20;
![]() = 4.
= 4.
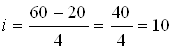
Тогда образуем четыре группы (Таблица 5):
Таблица 5
Статистический ряд распределения предприятий по среднегодовой стоимости основных производственных фондов
| Группы | Среднегодовая стоимость основных производственных фондов |
| 20-30 | 20 |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30-40 | 33 |
| 33 | |
| 35 | |
| 36 | |
| 37 | |
| 37 | |
| 38 | |
| 39 | |
| 40-50 | 41 |
| 41 | |
| 42 | |
| 44 | |
| 45 | |
| 46 | |
| 46 | |
| 47 | |
| 49 | |
| 49 | |
| 50-60 | 53 |
| 55 | |
| 55 | |
| 56 | |
| 56 | |
| 57 | |
| 60 |
Взвесим варианты признака по числу предприятий и по их удельному весу:
3.
![]() , где
, где
![]() - рентабельность капитала;
- рентабельность капитала;
![]() – прибыль;
– прибыль;
![]() – капитал.
– капитал.
а) ![]()
б)

![]()
в)
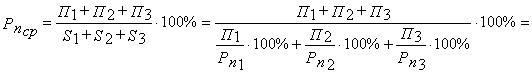
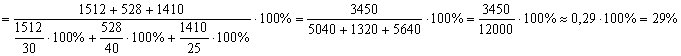
г)
![]() , где
, где
![]() - удельный вес акционерного капитала в общем объеме.
- удельный вес акционерного капитала в общем объеме.
Значит:
![]() ;
;
![]() ;
;
![]() .
.
Тогда:
![]() ;
;
![]() ;
;
![]() .
.
Подставим полученные формулы в формулу рентабельности акционерного капитала:
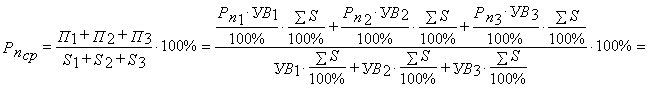

![]()
Ответ: 29%
Аналитическая частьИспользуя данные Таблицы 6 Численность экономически активного населения, занятых и безработных (тысяч человек) из Российского статистического ежегодника 2003 года (стр.129), найдем среднюю арифметическую простую величину, среднюю гармоническую простую величину, моду и медиану в дискретных рядах.
Таблица 6
Численность экономически активного населения, занятых и безработных (тысяч человек)
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | |
| Численность экономически активного населения - всего | 70861 | 69660 | 68079 | 67339 | 72175 | 71464 | 70968 | 71919 |
| мужчины | 37336 | 36749 | 35925 | 35379 | 37639 | 37154 | 36846 | 36937 |
| женщины | 33525 | 32911 | 32154 | 31960 | 34537 | 34310 | 34122 | 34982 |
| в том числе: | ||||||||
| занятые в экономике -всего | 64149 | 62928 | 60021 | 58437 | 63082 | 64465 | 64664 | 65766 |
| мужчины | 33720 | 33087 | 31554 | 30587 | 32838 | 33374 | 33435 | 33615 |
| женщины | 30429 | 29841 | 28467 | 27850 | 30244 | 31091 | 31229 | 32151 |
Средняя арифметическая простая величина:
Найдем среднюю численность экономически активного населения – всего за 1995-2002 годы.
![]()
Средняя гармоническая простая величина:
Найдем среднюю численность экономически активного населения – всего мужчин за 1995-2002 годы.
![]()
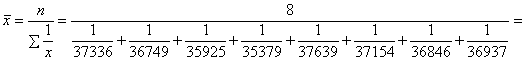
![]()
![]()
Мода в дискретном ряду:
Найдем моду ряда значений численности экономически активного населения, занятых в экономике за 1995-2002 годы.
Модой в дискретном ряду является величина признака, которой соответствует максимальная частота. В данном случае это 2002 год (65766 тысяч человек).
Полученный результат говорит о том, что в 2002 году была самая высокая численность экономически активного населения, занятых в экономике.
Медиана в дискретном ряду:
Найдем медиану ряда значений численности экономически активного населения, занятых в экономике мужчин.
Медианой в дискретном ряду является центральный член ранжированного ряда.
Упорядочим данный ряд.
30587; 31554; 32838; 33087; 33374; 33435; 33615; 33720.
В данном случае четный объем ряда, поэтому медиана равна средней из двух вариантов, находящихся в середине ряда.
![]()
Используя данные Таблицы 7 Распределение численности безработных по возрастным группам (в процентах к итогу) из Российского статистического ежегодника 2003 года (стр.142), найдем моду и медиану в интервальных рядах.
Таблица 7
Распределение численности безработных по возрастным группам (в процентах к итогу)
| до 20 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | |
| 2002 | 8,9 | 17 | 13,2 | 11,9 | 11,6 | 13,1 | 10,7 | 8,3 | 2,5 | 2,8 |
Мода в интервальном ряду:
Найдем моду интервального ряда значений численности безработных по возрастным группам в 2002 году.
Модальным рядом будет ряд 20-24 лет, т. к. именно ему соответствует наибольшая частота (17 %).
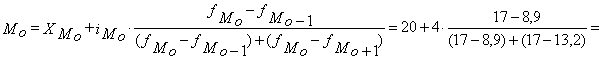
![]()
Полученный результат говорит о том, что в 2002 году самая высокая численность безработных приходилась на возраст 22,7 лет.
Это значение можно изобразить графически (рис. 1)
Медиана в интервальном ряду:
Найдем медиану интервального ряда значений численности безработных по возрастным группам в 2002 году.
Прежде всего найдем медианный интервал. Таким интервалом будет интервал численности безработных в возрасте 30-34, поскольку его кумулятивная частота равна 51 (8,9+17+13,2+11,9), что превышает половину суммы всех частот (100:2=50). Нижняя граница интервала 30; его частота 11,9; частота, накопленная до него, равна 39,1 (8,9+17+13,2); медианный интервал равен 4.
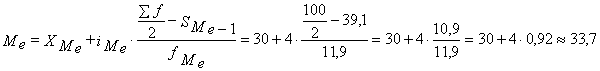
Полученный результат говорит о том, что из 100% безработных в 2002 году 50% имели возраст менее 33,7 года, а остальные 50% имели возраст более 33,7 года.
Рис. 1 Мода в интервальном ряду
Используя данные Таблицы 8 Численность населения в межпереписной период по регионам Российской Федерации (тысяч человек) из Российского статистического ежегодника 2003 года (стр.83), найдем среднюю арифметическую взвешенную величину.
Таблица 8
Численность населения в межпереписной период по регионам Российской Федерации (тысяч человек)
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | |
| Сибирский федеральный округ | 1084 | 1086 | 1086 | 1083 | 1075 | 1079 | 1078 | 1075 | 1074 | 1072 | 1068 | 1065 | 1061 | 1057 |
| Томская область |
Средняя арифметическая взвешенная величина:
Найдем среднюю численность населения в межпереписной период в Томской области с 1990 года по 2003 год.
Упорядочим все варианты:
| Сибирский федеральный округ | 1057 | 1061 | 1065 | 1068 | 1072 | 1074 | 1075 | 1078 | 1079 | 1083 | 1084 | 1086 |
| Томская область | ||||||||||||
| Весы | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 |
| f |
![]()
![]()
Используя данные Таблицы 9 Основные показатели аудиторской деятельности (человек) из Российского статистического ежегодника 2003 года (стр.83), найдем среднюю гармоническую взвешенную величину.
Таблица 9
Основные показатели аудиторской деятельности (человек)
| Средняя численность работников (включая внешних совместителей и работников несписочного состава), человек: | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Всего | 7582 | 12141 | 15675 | 15381 | 27303 | 20884 | 32787 | 25452 |
| В расчете на одну организацию | 7 | 7 | 8 | 7 | 10 | 7 | 9 | 4 |
Средняя гармоническая взвешенная величина:
Найдем среднюю численность человек, занимающихся аудиторской деятельностью, в расчете на одну организацию с 1995 года по 2002 год.
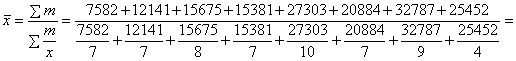
![]()
Используя данные Таблиц 10,11 Численность населения в межпереписной период по регионам Российской Федерации (тысяч человек) из Российского статистического ежегодника 2003 года (стр.82), найдем среднюю хронологическую величину ряда с равностоящими уровнями и неравностоящими уровнями.
Средняя хронологическая величина ряда с равностоящими уровнями:
Найдем среднюю численность населения в межпереписной период в Костромской области с 1996 года по 2003 год.
Таблица 10
Численность населения в межпереписной период по регионам Российской Федерации –Костромская область (тысяч человек)
| 1.I.96 | 1.I.97 | 1.I.98 | 1.I.99 | 1.I.00 | 1.I.01 | 1.I.02 | 1.I.03 | |
| Центральный федеральный округ | 800 | 795 | 791 | 787 | 781 | 774 | 766 | 758 |
| Костромская область |
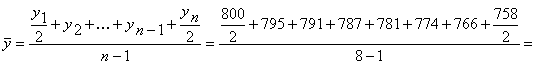
![]()
Средняя хронологическая величина ряда с неравностоящими уровнями:
Найдем среднюю численность населения в межпереписной период в Ненецком автономном округе с 1990 года по 2003 год.
Таблица 11
Численность населения в межпереписной период по регионам Российской Федерации – Ненецкий автономный округ (тысяч человек)
| 1.I.90 | 1.I.92 | 1.I.95 | 1.I.99 | 1.I.00 | 1.I.03 | |
| Северо-Западный федеральный округ | 54 | 53 | 49 | 46 | 45 | 46 |
| Ненецкий автономный округ |
![]()
![]()
Заключение
Средние величины имеют большое распространение в статистике коммерческой деятельности. В средних величинах отображаются важнейшие показатели товарооборота, товарных запасов, цен. Средними величинами характеризуются качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.
Правильное понимания сущности средней определяет ее особуюзначимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.
Средние величины — это обобщающие показатели, в которых находят выражения действие общих условий, закономерность изучаемого явления.
Статистические средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения (сплошного или выборочного).
В экономическом анализе использование средних величин является основным инструментом для оценки результатов научно-технического прогресса, социальных мероприятий, поиска резервов развития экономики. В то же время следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный
Список использованной литературы:
1. Афанасьев В.И. Метод средних в экономических расчетах. – М.:
Финансы и статистика, 1996. – 224с.
2. Балинова В.С. Статистика в вопросах и ответах: Учебное пособие. –
М.: Проспект, 2004. – 344с.
3. Гусаров В.М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ,
2001. – 463с.
4. Гусаров В.М. Теория статистики: Учеб. пособие для вузов. – М.:
Аудит, ЮНИТИ, 1998. – 247с.
5. Неганова Л.М. Статистика: Пособие для сдачи экзамена. – М.:
ЮРАЙТ, 2004. – 220с.
6. Неганова Л.М. Экзамен по статистике: Учеб. пособие для вузов. – М.: Приор-издат,2004. – 144с.
7. Российский статистический ежегодник. – М.:2003. – с.82,83,129,142.
Похожие работы
... расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени ...
... – М,1999. – 139 с. 4. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И.И.Елисеевой. – М.: Финансы и статистика, 1996. – 368 с.: ил. 5. Пасхавер И.С. Средние величины в статистике. – М.: Статистика, 1979. – 279 с., ил. 6. Практикум по теории статистики: Учеб. пособие / Под ред. Р.А. Шмойловой. – М.; Финансы и статистика, 2001. – 416 ...
... цену приобретения акций: Решение Воспользуемся для определения средней цены формулой (7): руб. В практике реальных расчетов взвешенные средние гармонические используются чаще. 4. Понятие, виды и показатели вариации Рассматривая зарегистрированные при статистическом наблюдении величины того или иного признака у отдельных единиц совокупности, обнаруживаем, что они различаются между ...
... 7. Могут ли индексы фиксированного состава и структурных сдвигов быть противоположными (один - увеличение, другой - уменьшение)? А) могут; Б) не могут. 8.Статистика продукции. Продукция промышленности и виды ее по степени готовности. Продукция промышленности – часть ВВП, создаваемая заведениями промышленных и непромышленных ...
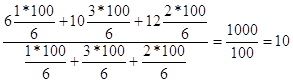
0 комментариев