Навигация
Методи обчислення дисперсії
План
1. Методи обчислення дисперсії
2. Задача №6
3. Задача №12
4. Задача №18
5. Задача №24
1. Методи обчислення дисперсії
Статистична дисперсія (від англ. statistical dispersion) — ступінь відхилення або зміни значень змінній від центрального пункту. Статистична дисперсія розраховується як різниця між значенням середньою квадратів варіюючої ознаки і квадратом середнього значення цієї ознаки. Дисперсія є базовим інструментом для статистичної оцінки варіації розподілу. Якщо значення ознаки розподілу ідентичні, то дисперсія рівна нулю. Дисперсія не може бути негативною величиною.
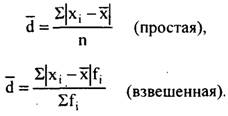
Умови існування і розвитку окремих одиниць сукупності певною мірою різні, що позначається і на відмінності значень у них узятої нами ознаки. Середня величина відображає ці середні умови.
Середнє лінійне відхилення дає узагальнену характеристику ступеня тієї, що коливається ознаки в сукупності. Проте при його численні доводиться допускати некоректні з погляду математики дії, порушувати закони алгебри, що спонукало математиків і статистиків шукати інший спосіб оцінки варіації для того, щоб мати справу тільки з позитивними величинами. Найпростіший вихід - звести всі відхилення в другий ступінь.
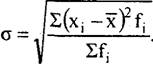
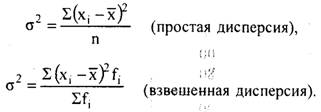
Отримана міра варіації називається дисперсією, а корінь квадратний з дисперсії - середнім квадратичним відхиленням. Ці показники є загальноприйнятими заходами варіації і часто використовуються в статистичних дослідженнях, а також в техніці, біології і інших галузях знань. Дані показники знайшли також своє широке застосування в міжнародній практиці обліку і статистичного аналізу, зокрема в системі національного рахівництва.
Середнє квадратичне відхилення - це узагальнююча характеристика розмірів варіації ознаки в сукупності. Воно виражається в тих же одиницях вимірювання, що і ознака (у метрах, тоннах, рублях, відсотках і т. д.).
Дисперсія - середній квадрат відхилень індивідуальних значень ознаки від їх середньої величини.
Серед безлічі варіюючих ознак, що вивчаються статистикою, існують ознаки, якими володіють одні одиниці сукупності і не володіють інші. Ці ознаки називаються альтернативними. Прикладом таких ознак є: наявність бракованої продукції, вчений ступінь у викладача вузу, робота по отриманій спеціальності і так далі. Варіація альтернативної ознаки кількісно виявляється в значенні нуля у одиниць, які цією ознакою не володіють, або одиниці у тих, які дану ознаку мають.
Хай р - частка одиниць в сукупності, що володіють даною ознакою (р = m/n); q - частка одиниць, що не володіють даною ознакою, причому р + q = 1. Альтернативну ознаку приймає всього два значення - 0 і 1 з вагами відповідно q і р. Обчислений середнє значення альтернативної ознаки по формулі середньої арифметичної:
![]()
Дисперсія альтернативної ознаки визначається по формулі:
![]()
Таким чином, дисперсія альтернативної ознаки рівна твору частки на доповнюючи цю частку до одиниці число. Корінь квадратний з цього показника відповідає середньому квадратичному відхиленню альтернативної ознаки.
Показники варіації альтернативних ознак широко використовуються в статистиці, зокрема при проектуванні вибіркового спостереження, обробці даних соціологічних обстежень, статистичному контролі якості продукції, у ряді інших випадків.
Буває необхідно прослідкувати кількісні зміни ознаки по групах, на які розділяється сукупність, а також і між групами. Таке вивчення варіації досягається за допомогою обчислення і аналізу різних видів дисперсії.
Виділяють дисперсію загальну, міжгрупову і внутрішньогрупову. Загальна дисперсія вимірює варіацію ознаки у всій сукупності під впливом всіх чинників, що зумовили цю варіацію.
Існує закон, що зв'язує три види дисперсії. Загальна дисперсія рівна сумі середньої з внутрішньогрупових і міжгруповою дисперсій:
![]()
![]()
Дане співвідношення називають правилом складання дисперсій. Згідно цьому правилу, загальна дисперсія, що виникає під дією всіх чинників, рівна сумі дисперсії, що з'являється під впливом всіх інших чинників, і дисперсії, що виникає за рахунок группировочного ознаки.
Знаючи будь-які два види дисперсій, можна визначити або перевірити правильність розрахунку третього вигляду.
2. Задача №6
Виробництво хімічних волокон і ниток становили, в млн. грн.:
| 2003 р. | 2004 р. | 2005 р. | |
| Штучні волокна і нитки | 2,3 | 1,6 | 3,5 |
| Синтетичні волокна і нитки | 2,7 | 2,4 | 4,8 |
Визначити по кожному волокну:
1. Базисні та ланцюгові темпи зростання та приросту.
2. Середньорічні темпи зростання та приросту.
Здійснити аналіз:
1. Зміни виробництва волокон по відношенню до минулого року.
2. Зміни виробництва волокон по відношенню до базисного року.

![]()
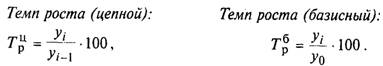
![]()
![]()
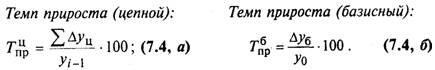
Среднегодовой темп роста выпуска товаров:
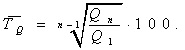
Среднегодовой темп прироста выпуска товаров:

|
Год | уц
| уб | Тц | Тб | Тц % | Тб % |
| 2003 | ----- | ----- | ----- | 1 | ----- | ----- |
| 2004 | -0,7 | -0,7 | 69,56 | 69,56 | -30,43 | -30,43 |
| -0,3 | -0,3 | 88,89 | 88,89 | -11,11 | -11,11 | |
| 2005 | 1,9 | 1,2 | 218,75 | 152,17 | 118,75 | 52,17 |
| 2,4 | 2,1 | 200 | 117,78 | 100 | 77,78 |
Рассчитываем среднегодовые темп роста и темп прироста по формулам
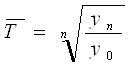
Среднегодовой темп роста
Похожие работы
... . Практикум. За ред. Єріної А.М., Пальянс З.А. – синій колір, стислий виклад теорії, приклад рішень, задачі. Рекомендується! 2. Ковтун Н.В., Столяров В,С. Загальна теорія статистики. Курс лекцій. К.: Хвиля, 1996. 3. Общая теория статистики. Учебник. Под общей редакцией проф. Елисеевой И.И. М.: Финансы и статистика, 1995. 4. Общая теория статистики. Учебник. Под редакцией Ефимовой М.Р. М.: 1996. 5. ...
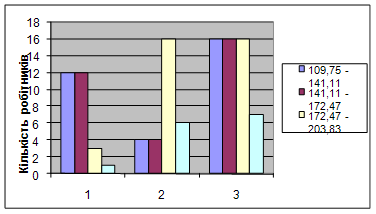
... івши розрахунки, я прийшла до таких висновків: - по 1-му цеху найбільше робітників І-ІІ розрядів зі стажем роботи 3-4років. Середня заробітна плата склала 158,11 грн. Половина робітників отримують зарплату нижче 137,70 грн., а половина - вищу. По 2-му рівна кількість працівників Ш-ІУ і V- VI розрядів, вона становить 13 чоловік. Загалом по заводу найбільше робітників III і IV розрядів; - По ...
... вдається вигравати у нього. Зрозуміло, що, вибравши першу стратегію, ви ризикуєте весь час грати на автоматі, що залишився, виграти на якому вам вдалося одного разу і, можливо, лише випадково. В області клінічних досліджень метод рандомізації, заснований на третій стратегії, носить назву «гра на лідера». Метод «гра на лідера» – перший пацієнт одержує методи лікування рівноімовірно, потім у ...
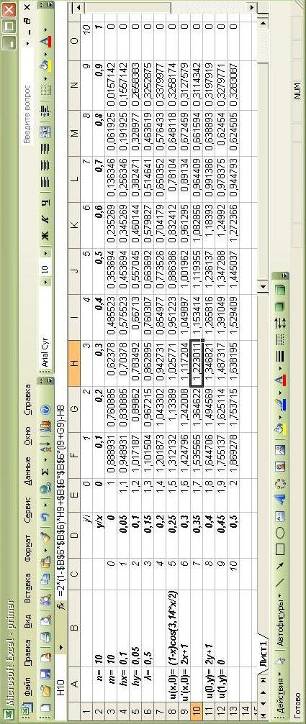
... за допомогою центральних різниць. Якщо область має форму кола, зручно користуватись полярними координатами Наведемо деякі загальні зауваження. При чисельному розв’язанні крайових задач для диференціальних рівнянь в частинних похідних методом сіток можуть бути використані тільки різницеві схеми, які збігаються, оскільки в цьому разі можна розраховувати на отримання наближеного розв’язку задачі, ...
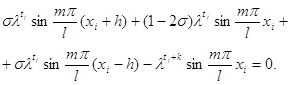
0 комментариев