Навигация
46 PROFIT FUNCTION (Ch. 3)
The a in the envelope theorem is p or w, and M(a) is n(p, w). According to the envelope theorem, the derivative of 7r(p, w) with respect to p is simply the partial derivative of the objective function, evaluated at the optimal choice:
9^1 =f(X)\ = /(*(*«,)).
Op x=x(p,w)
This is simply the profit-maximizing supply of the firm at prices (p, w).
Similarly,
dn{p, w)
—я = ~x =-x(p,w),
aw x=x(p,w)
which is the profit-maximizing net supply of the factor.
Comparative statics using the profit function
At the beginning of this chapter we proved that the profit function must satisfy certain properties. We have just seen that the net supply functions are the derivatives of the profit function. It is of interest to see what the properties of the profit function imply about the properties of the net supply functions. Let us examine the properties one by one.
First, the profit function is a monotonic function of the prices. Hence, the partial derivative of 7r(p) with respect to price i will be negative if good i is an input and positive if good i is an output. This is simply the sign convention for net supplies that we have adopted.
Second, the profit function is homogeneous of degree 1 in the prices. We have seen that this implies that the partial derivatives of the profit function must be homogeneous of degree 0. Scaling all prices by a positive factor t won't change the optimal choice of the firm, and therefore profits will scale by the same factor t.
Third, the profit function is a convex function of p. Hence, the matrix of second derivatives of 7r with respect to p—the Hessian matrix—must be a positive semidefinite matrix. But the matrix of second derivatives of the profit function is just the matrix of first derivatives of the net supply functions. In the two-good case, for example, we have
|
|
(dy,дш\
= dpidp2
I dy2dy2 I "
\ dp{op2 '
The matrix on the right is just the substitution matrix—how the net supply of good г changes as the price of good j changes. It follows from the properties of the profit function that this must be a symmetric, positive semidefinite matrix.
The fact that the net supply functions are the derivatives of the profit function gives us a handy way to move between properties of the profit function and properties of the net supply functions. Many propositions about profit-maximizing behavior become much easier to derive by using this relationship.
EXAMPLE: The LeChatelier principle
Let us consider the short-run response of a firm's supply behavior as compared to the long-run response. It seems plausible that the firm will respond more to a price change in the long run since, by definition, it has more factors to adjust in the long run than in the short run. This intuitive proposition can be proved rigorously.
For simplicity, we suppose that there is only one output and that the input prices are all fixed. Hence the profit function only depends on the (scalar) price of output. Denote the short-run profit function by ns(p,z) where z is some factor that is fixed in the short run. Let the long-run profit-maximizing demand for this factor be given by z(p) so that the long-run profit function is given by itl(p) = ^s{Pi z{p))- Finally, let p* be some given output price, and let z* = z(p*) be the optimal long-run demand for the 2-factor at p*.
The long-run profits are always at least as large as the short-run profits since the set of factors that can be adjusted in the long run includes the subset of factors that can be adjusted in the short run. It follows that
h(p) = nL(p) - ns(p, 2*) = ns(p, z(p)) - 7TS(p, z*) > 0
for all prices p. At the price p* the difference between the short-run and long-run profits is zero, so that h(p) reaches a minimum at p = p*. Hence, the first derivative must vanish at p*. By Hotelling's lemma, we see that the short-run and the long-run net supplies for each good must be equal at p*.
But we can say more. Since p* is in fact a minimum of h(p), the second derivative of h(p) is nonnegative. This means that
d2nL(p*) d2ns(p*,z*) >Q
dp2 dp2 ~
Using Hotelling's lemma once more, it follows that
dVLJP*) dys(p*,z*) = d2irL{p*) d2ns(p*,z*) >Q
dp dp dp2 dp2 ~
This expression implies that the long-run supply response to a change in price is at least as large as the short-run supply response at z* = z(p*).
Notes
The properties of the profit function were developed by Hotelling (1932), Hicks (1946), and Samuelson (1947).
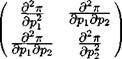
0 комментариев