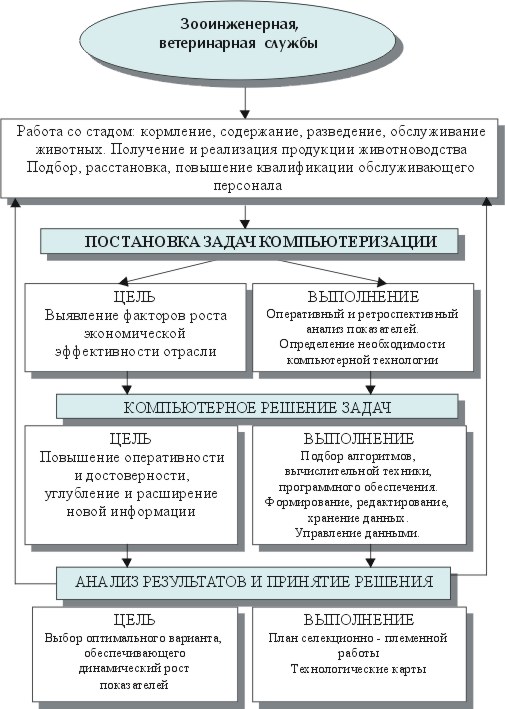
Навигация
Построение экономико-математической модели
3 Построение экономико-математической модели
За основные неизвестные в данной задаче принимается количество кормов и кормовых добавок, включаемых в суточный рацион,
X1 - отруби пшеничные
X2 - ячмень дробленый
Х3 - горох
X4 - комбикорм
X5 - витаминно-травяная мука
X6 - сено
X7 - солома
X8 - сенаж
X9 - силос кукурузный
X10 - жом
X11 - патока
X12 - премикс минерально-витаминный
Вспомогательная переменная X13 выражает общее содержание кормовых единиц в рационе, За единицу измерения основных переменных величин принят физический вес корма в килограммах (кг).
На переменные накладываются следующие группы ограничений:
· по содержанию питательных веществ в рационе;
· по пределам включения отдельных групп кормов в рацион;
· по соотношению отдельных видов кормов и добавок;
· по суммарному количеству кормовых единиц в рационе.
Основными ограничениями (1-15) являются условия по балансированию питательных веществ в рационе.
Технико-экономическими коэффициентами при основных переменных Xj в этих ограничениях являются показатели содержания питательных веществ в единице каждого вида корма (Таблица 1), а в правой части неравенств записывается потребное количество каждого вида питательных веществ для животных, необходимое для получения определенной продуктивности - Bi (Таблица 2).
Например, ограничение, требующее наличия в рационе 5,3 кормовых единиц, будет записано в следующем виде:
0,75x1+1,15x2+…….+0,76x11+0,5x12>=6,2 (1)
Ограничение по содержанию обменной энергии в рационе
8,85x1+10,5x2+……,+9,36x11>=54(2)
Ограничение по содержанию сухого вещества в рационе
0,85x1+0,85x2……+0,8x11>=6(3)
Ограничение по содержанию сырого протеина в рационе
151x1+113x2+…,,+99x11>=905(4)
Ограничение по содержанию переваримого протеина в рационе
97x1+27x2+……+60x11+ 55x12>=590(5)
Ограничение по содержанию сырой клетчатки в рационе
88x1+49x2+……+33x10>=1260(6)
Ограничение по содержанию сахара в рационе
47x1+22x2+……+626x11+25,5x12>=470(7)
Ограничение по содержанию сырого жира в рационе
41x1+22x2+……+3x10>=235(8)
Ограничение по содержанию кальция в рационе
2x1+2x2+……+3,2x11+133,6x12>=31(9)
Ограничение по содержанию фосфора в рационе
9,6x1+3,9x2+……+0,2x11+257,3x12>=18(10)
Ограничение по содержанию магния в рационе
4,3x1+1x2+……+0,1x11+27x12>=14(11)
Ограничение по содержанию каротина в рационе
2,6x1+0,2x2+……+20x9>=115(12)
Ограничение по содержанию кобальта в рационе
0,1x1+0,26x2+……+0,06x10+0,6x11+0,5x12>=3,6(13)
Ограничение по содержанию витамина Е в рационе
20,9x1+50x2+……+3x11>=150(14)
Ограничение по содержанию соли в рационе
81x12>=20(15)
Дополнительные ограничения (16-25) по пределам скармливания отдельных видов кормов или групп кормов.
Условие по минимальному и максимальному удельному весу концентратов в рационе имеет вид:
минимальная граница
(границы выбираются из таблицы 3 и делятся на 100 и записываются в виде коэффициента при х13) (при x4 – коэффициент 1, в данной записи его не пишут),
(не менее 20%/100=0,2) 0,75x1+1,15x2+1,18x3+x4>=0,2x13;
максимальная граница
(не более 31 %/100=0,31) 0,75x1+1,15x2+1,18x3+x4<=0,31x13,
Исходя из этого, преобразуя неравенство (перенесем х13 за знак неравенства), получим следующую запись данных ограничений:
0,75x1+1,15x2+1,18x3+x4-0,2x13>=0 ;(16)
0,75x1+1,15x2+1,18x3+x4-0,31x13<=0,
для приведения неравенства к типу «>=», преобразуем его в следующий вид
-0,75x1-1,15x2-1,18x3-x4+0,31x13>=0(17)
Ограничение по минимальному и максимальному включению в рацион грубых кормов:
0,48x6+0,34x7-0,10x13>=0(18)
-0,48x6-0,34x7+0,25x13>=0(19)
Ограничение по минимальному и максимальному включению в рацион силоса:
0,2x9-0,12x13>=0(20)
-0,2x9+0,23x13>=0(21)
Ограничение по минимальному и максимальному включению в рацион жома:
0,12x10-0,18x13>=0(22)
-0,12x10+0,3x13>=0(23)
Ограничение по минимальному и максимальному включению в рацион сенажа:
0,32x8-0,09x13>=0(24)
-0,32x8+0,19x13>=0(25)
В данных ограничениях коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма указанной группы, а коэффициентами при вспомогательной неизвестной являются нижние и верхние границы содержания отдельных групп кормов в рационе выраженных в долях единицы,
Ограничения по максимальной суточной даче отдельных кормов (26-28) имеют следующий вид (объем ограничений выбирается из таблицы 3):
Ограничение по максимальной суточной даче патоки (не более 2 кг).
x11<=2,3(26)
Ограничение по максимальной суточной даче ВТМ (не более 1,8 кг).
x5<=1,2(27)
Ограничение по максимальной суточной даче силоса (не более 30 кг).
x9<=26(28)
Ограничения (29-30) по включению отдельных видов кормов в состав группы кормов формулируют с использованием алгебраических преобразований. Так, ограничение по включению комбикорма в размере не менее 37% (таблица 3) от веса концентрированных кормов первоначально имеет такую форму:
x4 >=0,37*(0,75x1+1,15x2+1,18x3+x4),
а после преобразований оно приобретает следующий вид:
-0,37*0,75x1-0,37*1,15x2-0,37*1,18x3+(1-0,37)x4>=0;
перемножив коэффициенты, получим:
-0,278x1-0,426x2-0,437x3+0,63x4>=0(29)
Ограничение по включению сена в группу грубых кормов в размере не менее 39 % их питательности в начале будет записано так:
0,48x6 >= 0,39*(0,48x6+0,34x7),
(0,48- 0,39*0,48)х6- 0,39*0,34x7>=0
а в окончательной форме, перемножив коэффициенты, получим:
0,293x6-0,133x7>=0 , (30)
Вспомогательное ограничение 31 , обеспечивающее нахождение суммарного количества кормовых единиц в рационе, изначально имеет вид :
0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 = x13
а после преобразований оно приобретает следующий вид:
0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 – x13=0 (31)
В данном ограничении коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма (табл. 1), а по вспомогательной неизвестной –1,
Целевая функция (минимум себестоимости) представлена следующим образом:
Zmin=22x1+19x2+……+3,4x10+19x11+42x12
По неизвестным, обозначающим корма собственного производства, коэффициенты показывают себестоимость 1 кг корма, а по переменным, выражающим покупные корма и добавки, - цену приобретения (табл. 4).
В матричном (развернутом) виде разработанная экономико-математическая модель представлена в таблице 5.
4 Запись экономико-математической модели в структурном виде
Целевая функция:
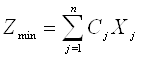 , где
, где
Cj – себестоимость или цена приобретения j-го вида корма;
Xj–искомое количествоj-го вида корма в составе суточного рациона,
Ограничения (условия):
1. Питательных веществ в рационе содержится не менее необходимого количества:
 , где
, где
Aij – содержание i–го питательного вещества в единице j-го вида корма;
Bi – суточная потребность животного в i–ом питательном веществе.
2. ![]()
Отдельные группы кормов включаются в рацион в зоотехнически обоснованных границах:
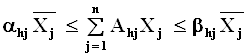 , где
, где
ahj , bhj – соответственно минимально и максимально допустимый удельный вес h-ой группы кормов в общей питательности рациона, выраженной в кормовых единицах;
Ahj – содержание кормовых единиц в единице измерения j-го вида корма h- ой группы кормо.,
3. В рационе соблюдаются соотношения отдельных видов кормов и кормовых добавок
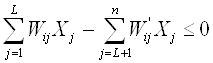 , где
, где
Wij, W'ij–коэффициенты пропорциональности между группами кормов.
4. Вспомогательного ограничения по общему количеству кормовых единиц в единиц в рационе
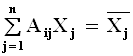 , где
, где
![]() – суммарное количество кормовых единиц в рационе.
– суммарное количество кормовых единиц в рационе.
5. Условие неотрицательности переменных
Xj >= 0, ![]() >=0
>=0
Таблица 5 Экономико-математическая модель по оптимизации рациона кормления

Дата:_________________ Подпись:____________________
Похожие работы
... одной копии программы данного класса варьирует в пределах от 800 до 2000 у.е.), есть смысл поиска более дешевых и доступных способов расчета рационов кормления сельскохозяйственных животных. Существенным недостатком специализированных программ является невозможность в случае необходимости быстрого совершенствования приложения, что снижает гибкость среды. В тоже время программа Lisa не обладает ...
... и справочной литературе. Используются также данные лабораторных анализов. Данная курсовая работа содержит ознакомительный теоретический материал и подробно расписанную задачу по составления оптимального рациона кормления скота. Задача содержит в себе пять подзадач для того, чтобы можно было проследить, как меняется рацион и оптимальная стоимость с теми или иными изменениями (ограниченность ...
... , каротину, макро- и микроэлементам. При учете всех вышеперечисленных условий наивысшая продуктивность животных позволит животноводческим фермам вести высокорентабельное хозяйство. Целью данной курсовой является оптимизация суточного рациона для дойных коров в СПК «Поя», т.е. создать оптимальный вариант рациона, для того чтобы коровы получили все необходимые питательные вещества и увеличили бы ...
... прохождения производственной практики. Цель курсового проекта. Выполняя проект по одной из тем курса студент должен показать умение владеть методологией и методикой экономико-математического моделирования для анализа экономических процессов в сельском хозяйстве с целью разработки оптимальных планов развития и повышения эффективности производства. Организация выполнения курсового проекта ...


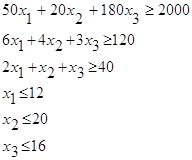
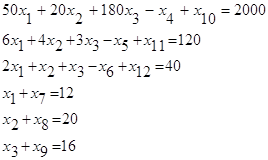
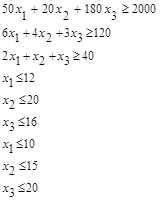
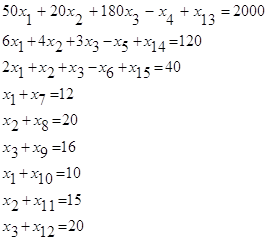
0 комментариев