Статистика

Зміст.

 

Питання 10.Поняття про статистичний показник. 4

Значення, функції статистичного показника. 4

Абсолютні та відносні величини. 6

Середні величини. 9

Показники варіації. 12

Задача 13. 15

Задача 45. 16

Задача 22. 17

Задача 37. 20

Література. 21

 

Питання 10.Поняття про статистичний показник. Значення, функції статистичного показника.

Після зведення і групування даних спостереження переходять до останнього – третього етапу статистичної методології. Він полягає в подальшій обробці статистичних таблиць шляхом обчислення статистичних показників.

Статистичний показник – це узагальнююча характеристика явища або процесу, яка характеризує всю сукупність одиниць обстеження і використовується для аналізу сукупності в цілому. За допомогою статистичних показників вирішується одна з головних задач статистики: визначається кількісна сторона явища чи процесу у поєднанні з якісною стороною. Кількісний бік показника представляється числом з відповідною одиницею виміру для характеристики: розміру явищ (кількості робітників, обсягу товарообороту, капіталу фірми тощо); їх рівнів (рівня продуктивності праці робітників тощо); співвідношень ( наприклад, між продавцями та іншими категоріями працівників магазину). Якісний зміст показника залежить від суті досліджуваного явища (процесу) і відображається у назві показника (прибутковість, народжуваність тощо).

Показники поділяються на види в залежності від способу їх обчислення, ознак часу, виконання своїх функцій.

За способом обчислення розрізняють первинні і похідні показники. Первинні визначаються шляхом зведення та групування даних і подаються у формі абсолютних величин (наприклад, кількість та сума вкладів громадян у банку). Похідні показники обчислюються на базі первинних і мають форму середніх або відносних величин (наприклад, середня заробітна плата, індекс цін).

Серед статистичних показників окрему групу становлять взаємообернені показники – пара характеристик, які існують паралельно і відповідають одному й тому ж явищу (процесу). Це прямий показник "х", який змінюється у напрямі зміни явища (наприклад, продуктивність праці за одну одиницю часу), та обернений  - у протилежному напрямі (наприклад, трудомісткість одиниці продукції).

За ознакою часу показники поділяються на інтервальні та моментні. Інтервальні характеризують явище за певний період часу (місяць, квартал, рік): наприклад, середньомісячні сукупні витрати на душу населення. Моментні показники характеризують явище за станом на певний момент часу (дату): наприклад, залишок обігових коштів на початок місяця.

З способом виконання своїх функцій розглядають показники, що відбивають обсяг явища, його середній рівень, інтенсивність прояву, структуру, зміну в часі або порівнянні у просторі.

За суттю досліджуваних явищ розрізняють об'ємні показники, що характеризують розміри явищ, процесів, та якісні показники, що характеризують кількісні співвідношення, характерні властивості досліджуваних явищ.

За ступенем агрегування явищ можна розглядати індивідуальні показники, що виражають розміри ознаки окремих одиниць сукупності та загальні (узагальню вальні) показники, що виражають розміри ознаки окремих груп або всієї сукупності.

В статистиці використовують декілька різновидів статистичних показників:

Ä  Абсолютні та відносні величини;

Ä  Середні величини;

Ä  Показники варіації.

Щоб статистичні показники правильно характеризували явище, що розглядається, необхідно виконувати такі вимоги:

1)  спиратися при їх побудові на положення економічної теорії, статистичну методологію, досвід статистичних робіт;

2)  добиватися повноти статистичної інформації як за охопленням одиниць об’єкта, так і за комплексним відображенням усіх сторін процесу, що вивчається;

3)  забезпечувати зіставлення статистичних показників за рахунок подібності вихідних даних за часом та у просторі;

4)  забезпечувати точність та надійність вихідної інформації для достовірності змісту процесу, що досліджується.

Функції статистичних показників: пізнавальна, управлінська, контрольна, стимулювальна.

Статистичні показники є базою для аналізу та прогнозування соціально-економічного розвитку держави, її окремих галузей і регіонів, стану й розвитку досліджуваних явищ, напряму та інтенсивності процесів, що відбуваються в суспільстві. Вивчаючи явища кількісно, економіст аналізує їх, пізнає якісно, проникає в сутність. У цьому й проявляється пізнавальна функція статистичних показників.

Управлінська функція статистичних показників полягає в тому, що вони є важливим елементом процесу управління на всіх його рівнях. З розвитком ринкових відносин ця роль статистичних показників зростає. Підвищується значення й контрольної функції статистичних показників, насамперед – за виконанням договірних умов.

Статистичні показники як відображення об’єктивної реальності тісно пов’язані між собою, тому їх розглядають не ізольовано один від одного, а в певному взаємозв’язку. Наприклад, для характеристики діяльності промислового підприємства потрібно розглядати кілька показників, які перебуваючи у певному взаємозв’язку, утворюють систему статистичних показників.

Абсолютні та відносні величини.

 

Абсолютними величинами в статистиці називають кількісні показники, які вивчають рівень, обсяг, чисельність вивчаємих суспільних явищ.

За способом вираження вивчаємого явища абсолютні величини поділяють на індивідуальні та загальні (сумарні).

Абсолютні показники можуть виражати розміри, обсяги та рівні суспільних явищ на певний момент або період часу.

Абсолютні величини – це іменовані числа і в залежності від характеру явища або процесу можуть мати різні одиниці вимірювання: натуральні; умовно-натуральні; трудові; вартісні.

Абсолютні показники відіграють важливу роль у системі узагальнюючих статистичних показників. В той же час вони не можуть достатньо певного уявлення про досліджуване явище. Тому виникає потреба в обчисленні інших узагальнюючих показників – відносних та середніх величин, підґрунтям для яких є абсолютні величини.

Відносні величини – це узагальнюючі кількісні показники, які виражають співвідношення порівнюваних абсолютних величин.

Логічною формулою відносної величини є така звичайна дріб:

В залежності від величин чисельника та знаменника цього дробу відносні величини можуть бути виражені у таких формах: коефіцієнтах (частках), процентах (%), проміле (‰), продеціміле (⁰/₀₀₀), коли за базу порівняння приймають відповідно 1, 100, 1000, 10000 одиниць.

Різноманітність співвідношень у реальному житті потребує різних за змістом і статистичною природою відносних величин. В залежності від своїх функцій, що виконують відносні величини при проведенні аналізу, ці величини можна класифікувати так:

Відношення однойменних показників:

1)  відносні величини динаміки;

2)  відносні величини структури;

3)  відносні величини координації;

4)  відносний показник планового завдання;

5)  відносний показник виконання плану;

6)  відносні показники порівняння.

Відношення різнойменних показників:

7)  відносні величини інтенсивності;

8)  відносні величини диференціації.

Відносна величина динаміки.

Динамікою у статистиці називають зміну соціально-економічного явища в часі. Відносна величина динаміки характеризує напрям та інтенсивність зміни показника за часом і визначається співвідношенням його значень за два періоди або моменти часу. При цьому базою порівняння може бути змінний попередній рівень (розрахунок ланцюговим способом) або постійний віддалений за часом рівень (розрахунок базисним способом). Відносні показники динаміки називають темпами зростання.

Відносна величина структури.

Статистичні сукупності завжди структуровані і мають певні складові. Відносна величина структури характеризує склад, структуру сукупності за тією чи іншою ознакою і показує внесок складових сукупності до загальної маси. Вона визначається співвідношенням розмірів складових частин сукупності до загального підсумку. Скільки складових, стільки відносних величин структури. Вони визначаються простим чи десятинним дробом або процентом

Відносна величина координації.

Відносна величина характеризує структурованість сукупності. Відносна величина координації дає співвідношення різних структурних одиниць тієї самої сукупності і показує, скільки одиниць однієї частини сукупності припадає на 1, 100, 1000 і більше одиниць іншої, взятої за базу порівняння.

Відносні показники планового завдання та виконання плану.

Відносний показник планового завдання – відношення величини показника, встановленого на плановий період, до його величини, досягнутого за попередній період, який взято за базу зрівняння.

Відносний показник виконання плану являє собою відношення фактично досягнутого рівня до планового завдання.

Відносні показники динаміки (К), планового завдання (К_пз) та виконання плану (К_вп) пов’язані між собою таким рівнянням: К = К_пз × К_вп.

Відносні величини порівняння.

Відносна величина порівняння у звичайному розумінні характеризує порівняння однойменних показників, що стосуються різних об’єктів, взятих за той самий період чи момент часу. Обчислюється у відносних величинах або процентах.

 До цього виду відносних показників належать відносні величини просторового порівняння та відносні величини порівняння зі стандартом.

Відносна величина просторового порівняння – це відношення розмірів або рівнів однойменних показників за різними територіями чи об’єктами. Найчастіше це регіональні чи міжнародні порівняння показників економічного розвитку або життєвого рівня. Базою порівняння може бути будь-який об’єкт. Головне, щоб методика розрахунку порівнюваних показників була однаковою.

Відносна величина порівняння зі стандартом являє собою порівняння фактичних значень показників з певним еталоном – стандартом, нормативом, оптимальним рівнем. Такими відносними величинами порівняння є виконання договірних зобов’язань, використання виробничих потужностей тощо.

Відносна величина інтенсивності.

Відносна величини інтенсивності характеризує відношення різнойменних величин, зв’язаних між собою певним чином. Це – щільність населення на 1 кв. км, виробництво електроенергії на душу населення тощо. Якщо обсяги явища незначні відносно обсягів середовища, то їх співвідношення збільшуються у 100, 1000, 10000 і більше разів. Наприклад, показники народжуваності, смертності, шлюбності розраховуються на 1000 осіб населення, забезпеченість населення лікарями – на 10000 осіб населення, захворюваність та злочинність – на 100000 осіб населення.

Відносна величина диференціації.

Відносна величина диференціації обчислюється в результаті порівняння двох структурних рядів, один з яких характеризує співвідношення частин сукупності за чисельністю одиниць, а другий – за величиною будь-якої ознаки.

Середні величини.

Середньою величиною в статистиці називаються кількісний показник характерного, типового рівня масових однорідних явищ, який складається під впливом загальних причин і умов розвитку. У зв’язку з цим середні величини відносяться до узагальнюючих статистичних показників, які дають зведену, підсумкову характеристику масових суспільних явищ. В середній величині гасяться (розчиняються) всі відмінності та особливості індивідуальних значень ознак і вона є "рівнодіючою" значень цих ознак. Головними умовами застосування середніх величин є:

1)  наявність якісної однорідності сукупності;

2)  масовий характер даних сукупності, де діє закон великих чисел.

Залежно від характеру ознаки, що усереднюється, і наявності вихідної статистичної інформації в статистиці використовують декілька видів середніх, серед яких є найбільш поширені: середня арифметична, середня гармонічна, середня квадратична, середня геометрична. Поряд з переліченими видами середніх величин у статистичній практиці застосовують також середню хронологічну та структурні середні: моду і медіану. Використання того чи іншого виду середніх залежить від двох обставин:

1)  від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні);

2)  від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загального обсягу (сума, добуток, степінь, квадратичний корінь).

Кожна із зазначених видів середніх може виступати у двох формах: простої та зваженої. Проста середня застосовується при обчисленні середньої за первинними (не згрупованими) даними, зважена – за згрупованими даними.

При виконанні середніх величин використовуються такі позначення:

 - середнє значення досліджувальної ознаки;

х_і або х – кожне індивідуальне значення усереднюваної ознаки (варіанта) в варіаційному ряді;

f_і або f – частота повторень (вага) індивідуальної ознаки в варіаційному ряді;

z = xf – обсяг значень ознаки;

n – кількість одиниць досліджуваної ознаки.

Середня арифметична.

Середня арифметична – це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:

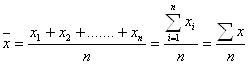
Зважена середня арифметична використовується у тих випадках, коли значення ознаки подано у вигляді варіаційного ряду, в якому чисельність одиниць у варіантах не однакова:

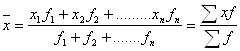
 З формули видно, що середня зважена принципово не відрізняється від середньої простої арифметичної. Тут додавання f разів варіанти x змінюється множенням її на кількість повторень (f).

Середня гармонічна.

Середня гармонічна – це обернена до середньої арифметичної із обернених значень ознак. Її обчислюють, коли необхідно осереднення обернених індивідуальних значень ознак шляхом їх підсумування. У випадку розрахунку середньої гармонійної зваженої її обчислюють тоді, коли відомі дані про загальний обсяг ознаки (z = xf), а також індивідуальні значення ознаки (х), невідома частота (f). Формули мають такий вигляд:

- для простої

- для зваженої .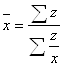

Середня квадратична.

Середня квадратична використовується для визначення показників варіації (коливання) ознаки – дисперсії та середнього квадратичного відхилення. Обчислюється на основі квадратів відхилень індивідуальних значень ознаки від їх середньої величини. Формула:

-  проста ;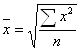

-  зважена

Середня геометрична.

Середню геометричну застосовують у тих випадках, коли обсяг сукупності формується не сумою, а добутком індивідуальних значень ознак. Цей вид середньої використовується здебільшого для обчислення середніх коефіцієнтів (темпів) зростання в рядах динаміки. Так, у випадку однакових часових інтервалів між рівнями динамічного ряду середня геометрична проста має такий вигляд:

де  - темпи зростання, y_і, y_і-1 – відповідно розглядаємий та попередній рівні ряду, n – кількість інтервалів.

 

Мода і медіана.

Середніми величинами в статистичних рядах розподілу є мода і медіана, які відносяться до класу структурних (позиційних) середніх. Їх величини залежать лише від характеру частот, тобто від структури розподілу. На відміну від інших середніх, які залежать від усіх значень ознаки, мода і медіана не залежить від крайніх значень Це особливо важливо для незакритих крайніх інтервалів варіаційних рядів розподілу.

Мода (М_о) – це значення варіанти, що найчастіше повторюється в ряду розподілу. Спосіб обчислення моди залежить від статистичного ряду. Для атрибутивних і дискретних рядів розподілу моду визначають візуально без будь-яких розрахунків за значеннями варіанти з найбільшою частотою. В інтервальному ряді спочатку визначається модальний інтервал (інтервал з найбільшою частотою) і значення моди в середині інтервалу розраховується за формулою:

де х₀ – нижня межа модального інтервалу;

h – величина модального інтервалу;

f₁, f₂, f₃ – частота відповідно перед модального, модального та після модального інтервалів.

Медіана (М_е) – варіанта, що ділить ранжируваний ряд на дві рівні за обсягом частини. Медіана для дискретного ряду з непарним числом варіант буде відповідати середній варіанті М_е = х_m-1, де m – номер кратної варіанти першої половини ранжируваного ряду. Медіана для дискретного ряду з парним числом варіант буде відповідати середній із значень варіант у ранжируваному ряду: . Для інтервального ряду медіана обчислюється для середини медіанного інтервалу, за який приймається такий, де сума накопичених частот перевищує половину значень частот ряду розподілу. В даному випадку використовується така формула:  

де х₀ – нижня межа медіанного інтервалу; h – величина медіанного інтервалу; 0,5 ∑f – половина суми накопичених частот інтервального ряду; S_х0 – сума накопичених частот перед медіанним інтервалом; f_m­ – частота медіанного інтервалу.

В аналізі закономірностей використовуються такі характеристики як квартилі та децилі. Квартилі – це варіанти, які поділяють обсяги сукупності на чотири рівні частини, децилі – на десять частин.

Показники варіації.

Після встановлення середньої величини (,М_о, М_е) виникає питання, в якій мірі індивідуальні значення ознаки відрізняються між собою та від середньої. Для цього розраховують показники варіації.

Варіацією ознаки називають різницю у числових значеннях ознак одиниць сукупності та їх коливання навколо середньої величини, що характеризує сукупність. Чим менша варіація, тим одноріднішою є сукупність і більш надійною (типовою) є середня величина.

До основних абсолютних і відносних показників, що характеризують варіацію, є такі: розмах варіації, середнє лінійне відхилення, дисперсія, середнє квадратичне відхилення, коефіцієнт варіації тощо.

Розмах варіації – це різниця між найбільшим і найменшим значеннями ознаки: R = x_max – x_min.

Величина показника залежить тільки від крайніх значень ознаки і не враховує всіх значень, що містяться між ними.

Досконалішим є визначення варіації через інші показники, які дають змогу усунути недолік розмаху варіації.

Середнє лінійне відхилення являє собою арифметичну з абсолютних значень усіх відхилень індивідуальних значень ознаки від середньої:

а) просте: ;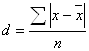

б) зважене: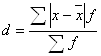

Наявність абсолютних значень відхилень від середньої пояснюються ат: середня арифметична має нульову властивість, згідно якої сума відхилень індивідуальних значень ознаки зі своїми знаками дорівнює нулю; щоб мати суму всіх відхилень, відмінних від нуля, кожне з них слід брати за абсолютною величиною.

Основним недоліком середнього лінійного відхилення є те, що в ньому не враховуються знаки відхилень, тобто їх спрямованість. Тому цей показник варіації використовується рідко. Дисперсія та лінійне квадратичне відхилення усувають недоліки середнього лінійного відхилення.

Дисперсією називають середню арифметичну квадратів відхилень індивідуальних значень ознаки. В залежності від вихідних даних дисперсія може обчислюватись за формулами середньої арифметичної простої або зваженої:

а) проста: ;

б) зважена: .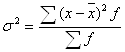

Дисперсія – це один з найбільш розповсюджених в економічній практиці узагальнюючих показників розміру варіації у сукупності. Дисперсію використовують не лише для оцінки варіації, а й для вимірювання зв’язків між досліджувальними факторами; розклад дисперсії на складові дозволяє оцінити вплив різних факторів, які обумовлюють варіацію ознаки.

Середнє квадратичне відхилення, як і дисперсія, виступає в якості широко використовуваного узагальнюючого показника варіації. Його обчислюють, здобувши квадратичний корінь з дисперсії:

а) просте: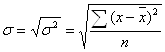

б) зважене: .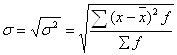

Смислове значення середнього квадратичного відхилення таке саме, як і лінійного відхилення: воно показує, на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього значення. Перевага цього показника порівняно із середнім лінійним відхиленням полягає у відсутності умовного припущення з сумування відхилень без врахування їх знаків, бо відхилення використовують у квадратній степені. Крім зазначеного, перевагою даного показника у зрівнянні з дисперсією є те, що середнє квадратичне відхилення виражається в тих же одиницях вимірювання, що і значення досліджувальної ознаки. Тому цей показник називають також стандартним відхиленням.

В статистичній практиці часто виникає необхідність порівняння варіацій різних ознак. При таких порівняннях показники коливання ознак з різними одиницями вимірювання не можуть бути використані.

Для здійснення такого роду порівнянь, а також при зіставленні ознаки у декількох сукупностях з різними середніми арифметичними використовують відносний показник варіації – коефіцієнт варіації.

Коефіцієнтом варіації називають процентне відношення середнього квадратичного відхилення до середньої арифметичної величини ознаки:

Чим більший коефіцієнт варіації, тим менш однорідна сукупність і тим менш типова середня для даної сукупності. Встановлено, що сукупність кількісно однорідна, якщо коефіцієнт не перевищує 33%.

Дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ і є важливим елементом статистичних методів, зокрема у дисперсному аналізі.

У структурованій сукупності, яка поділена на m груп за факторною ознакою х, загальна дисперсія σ² результативної ознаки у, може бути представлена складовими: між групова дисперсія δ²та середня з групових дисперсій  . Згідно з правилом розкладання дисперсій має місце рівняння:

.

Загальна дисперсія σ² вимірює варіацію результативної ознаки в цілому за сукупністю під впливом усіх факторів, які обумовлюють цю варіацію. Загальна дисперсія для зваженої результативної ознаки y обчислюється за формулою: .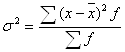

Між групова дисперсія δ² характеризує варіацію ознаки y за рахунок фактора х, покладеного в основу групування, і розраховується за формулою: 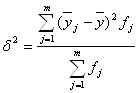, де  - відповідно середня j-ї групи та загальна середня варіюючої ознаки;  - чисельність одиниць (частота) j-ї групи.

Для розрахунку середньої з групових дисперсій з початку обчислюється внутрішньо групова дисперсія, яка характеризує варіацію результативної ознаки за рахунок інших факторів, не врахованих у групуванні:

 , де у_j - значення ознаки окремих елементів сукупності.

Для всіх груп в цілому розраховується середня з групових дисперсій, зважених на частоти відповідних груп:

.

Користуючись правилом розкладання дисперсій, можна за двома відомими дисперсіями знайти третю – невідому, а також мати уяву про силу впливу групувальної ознаки.

Задача 13.

Продуктивність праці у звітному періоді підвищилась порівняно з попереднім періодом на 17% при плановому завданні 115%. Визначить виконання плану з росту продуктивності праці.

Розв’язання.

За наведеними даними ми можемо сказати, що у звітному періоді виконання плану становило 117%, бо базисний період у порівнянні зі звітним розраховують завжди як 100%. Таким чином ми маємо дані: фактичні дані виконання плану у звітному періоді (117%) і планове завдання звітного періоду(115%), тобто дві абсолютні величини.

Тепер нам необхідно знайти відносну величину – узагальнюючий кількісний показник, який виражає співвідношення порівнюваних абсолютних величин.

Логічна формула відносної величини:

Згідно з завданням нам треба визначити відносний показник виконання плану – відношення фактично досягнутого рівня до планового завдання.

Коефіцієнт виконання плану становить 1,02, що дорівнює 102 відсоткам. Це означає, що план фактично перевиконано у порівнянні до планового завдання на 2%.

Задача 45.

За наведеними даними визначте середню частку кредитів під заставу майна у загальній сумі кредиторської заборгованості банків. Обґрунтувати вибір форми середньої.

Відділення комерційних банків	Загальна сума кредиторської заборгованості, млн. грн.	Частка кредитів під заставу майна у загальній сумі кредиторської заборгованості, %.
Центральний	870	30
Філії	926	30
Всього	1796	?

Розв'язання.

Середня арифметична – це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:

 

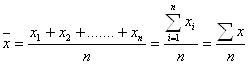
В нашому випадку це можна розрахувати таким чином:

%

або: якщо загальна сума кожної кредиторської заборгованості це 100%, то

1)  870/100×30=261

2)  926/100×30=277,8

Відділення комерційних банків	Загальна сума кредиторської заборгованості, млн. грн.	Частка кредитів під заставу майна у загальній сумі кредиторської заборгованості, грн.
Центральний	870	261
Філії	926	277,8
Всього	1796	538,8

Розрахунки можна перевірити за допомогою звичайного алгебраїчного рівняння:

 тоді

Висновок: середня частка кредитів під заставу майна у загальній сумі кредиторської заборгованості банків становить 30%.

Задача 22.

Споживання палива тепловими електростанціями становило:

Вид палива, млн. т (газ – млн. м3)	Минулий рік	Поточний рік	Коефіцієнт переводу в умовне паливо
Вугілля	24,5	44,8	0,9
Мазут	41,3	36,2	1,37
Газ природний	28,7	35,6	1,2

Визначити: а) обсяги споживного палива за кожен рік; б) структуру споживного палива.

Зробити висновки щодо структурних зрушень.

Розв'язання.

Види палива, зазначені в таблиці, неоднорідні за своєю суттю. Щоб визначити загальні обсяги споживного палива нам потрібно перевести всі види палива в умовне паливо за допомогою коефіцієнту переводу.

1)  24,5×0,9=22,05

2)  41,3×1,37=56,58

3)  28,7×1,2=34,44

4)  44,8×0,9=40,32

5)  36,2×1,37=49,59

6)  35,6×1,2=42,72

7) 

Вид палива, млн.. т (газ – млн.. м3)	Минулий рік	Умовне паливо, минулий рік.	Поточний рік	Умовне паливо, поточний рік.	Коефіцієнт переводу в умовне паливо
Вугілля	24,5	22,05	44,8	40,32	0,9
Мазут	41,3	56,58	36,2	49,59	1,37
Газ природний	28,7	34,44	35,6	42,72	1,2
Всього	х	113,07	х	132,63	х

Сумуючи отримані дані ми можемо визначити обсяги споживного палива за кожен рік: минулий рік споживання становить 113,07 млн. умовного палива, поточний рік споживання становить 132,63 млн. умовного палива.

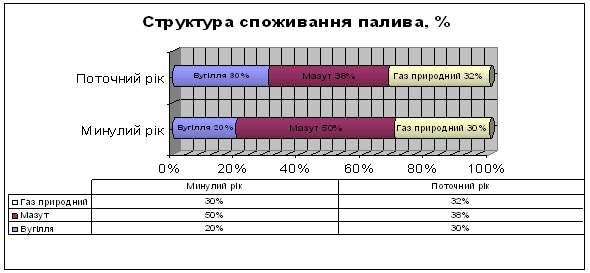
Для статистичного дослідження складу сукупності використовують структурні діаграми – діаграми співвідношення питомої ваги, які характеризують відношення окремих частин сукупності у загальному їх обсязі.

За розрахованими даними і за допомогою Microsoft Excel створюємо стовпчикові діаграми для зображення структури і структурних зрушень споживного палива.

За допомогою цієї діаграми (рис. 1), побудованої на значеннях обсягу в млн. у.п., ми можемо зробити висновок, що в цілому найбільшу частку палива, яке споживається на протязі року займає мазут, а найменшу – вугілля. Досить чітко можна розрізнити істотне підвищення споживання загального обсягу палива взагалі і його часток.

Розраховані дані переводимо у відсотки для зображення на структурній діаграмі.

Розраховуємо структуру споживного умовного палива (у.п.) минулого року.

Загальний обсяг минулого року – 100% = 113,07 млн. у.п.

1)  - вугілля;

2)  - мазут;

3)  - газ природний.

Розраховуємо структуру споживного умовного палива (у.п.) поточного року.

Загальний обсяг поточного року – 100% = 132,63 млн. у.п.

1)  - вугілля;

2)  - мазут;

3)  - газ природний.

За допомогою цієї діаграми (Рис. 2) ми можемо проаналізувати структуру споживного палива, співвідношення питомої ваги кожного виду палива в загальному обсязі за кожен окремий рік споживання.

Також можна зробити висновок, що споживання мазуту в поточному році суттєво зменшилося порівняно з минулим роком, при тому, що його обсяг споживання порівняно з іншими видами палива за поточний рік залишився домінуючим.

Споживання природного газу порівняно з минулим роком збільшилось несуттєво, а споживання вугілля порівняно з минулим роком збільшилось на третину.

Рис. 1.

Рис. 2

Задача 37.

Відома інформація: два квадрата зі сторонами 20 і 30 см. Визначте середню сторону квадрата.

Розв'язання.

Відомо, що квадрат складається з чотирьох сторін.

Таким чином у нас є варіанти: 20 і 30 см, які мають по чотири частоти.

Ми можемо використати для розрахунків формулу середньої арифметичної простої та середньої арифметичної зваженої:

а) проста -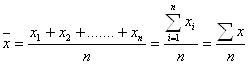

б) зважена -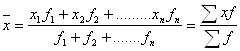

Розв'язання для першого варіанту:

Розв'язання для другого варіанту:

Середня сторона для кожного окремого квадрата:

1)  - перший квадрат.

2) - другий квадрат.

Висновок: середня сторона на обидва дорівнює 25 см, а середні сторони кожного окремого квадратів дорівнюють 20 і 30 см.

Література.

1.  Статистика: Підручник / Лугінін О.Є., Білоусова С.В. – Центр навчальної літератури, 2005. – 580 с.

2.  Теорія статистики: Навчальний посібник / Машков П.Г., Пастер П.І., Сторожук В.П., Ткач Є.І. – 20-ге вид., стереотип. – К.: Либідь, 2004 – 320 с.

3.  Бек В.Л. Теорія статистики: Навчальний посібник. – К.: ТОВ "Центр учбової літератури", 2002, с. 85-94.

4.  Гончарук А.Г. Основи статистики: Навчальний посібник. К.: Вища школа, 1994. – 448 с.

5.  Кулинич О.І. Економічна статистика: Навчальний посібник. – Хмельницький: Поділля, 2000. – 286 с.