Учитель повинен діагностувати, прогнозувати і планувати домашнє навантаження учнів, дотримуватися нормативів максимального навантаження школярів

4.  Учитель повинен діагностувати, прогнозувати і планувати домашнє навантаження учнів, дотримуватися нормативів максимального навантаження школярів.

"Кожний урок повинен бути для наставника завданням, до виконання якого він прагне, обдумуючи його завчасно: кожним завданням необхідно чогось досягти, зробити подальший крок і змусити весь клас зробити цей крок…" - К.Д. Ушинський.

У підготовці учителя до уроку виділяється три етапи: діагностика, прогнозування, планування. При цьому передбачається, що учитель добре знає фактичний матеріал, впевнено володіє ним, у нього немає проблем з освітніми завданнями.

Діагностика зводиться до уточнення всіх обставин проведення уроку: можливостей учнів, мотивів їхньої діяльності та поведінки, інтересів і здібностей, запитів і нахилів, рівня підготовки, характеру навчального матеріалу, його особливостей, структури уроку, а також аналізу всіх витрат часу в навчальному процесі — на актуалізацію опорних знань, засвоєння нового матеріалу, закріплення і систематизацію, контроль і корекцію знань, умінь. Результатом діагностики повинна бути діагностична карта уроку.

Прогнозування забезпечує оцінку різних варіантів проведення майбутнього уроку і вибір з них найоптимальнішого.

Планування — завершальна стадія підготовки, в ході якої створюється план управління пізнавальною діяльністю учнів. У плані молодого учителя повинні відображатися такі моменти:

— дата проведення уроку і його номер за тематичним планом;

— назва теми уроку і класу, в якому він проводиться;

— цілі і завдання освіти, виховання і розвитку учнів;

— структура уроку з вказівкою послідовності його етапів і приблизного розподілу часу за ними;

— зміст навчального матеріалу;

— методи і прийоми роботи учителя в кожній частині уроку;

— навчальне обладнання, необхідне для проведення уроку;

— домашнє завдання.

План-конспект повинен бути детальним. Ця вимога виведена з практики: нікому ще не вдалося стати майстром без осмислення в усіх подробицях організації уроку, який має проводитися.

Отже, вчасно і повноцінно сформовані вміння та навички самостійної праці в початкових класах допомагають класоводові підтримувати інтерес до навчання. Завдяки цьому діти працюють активно, щоразу роблячи для себе невеликі, але важливі відкриття у Країну Знань.

Розділ ІІ. Методика організації самостійної роботи на уроках математики в початкових класах

 

ІІ.1 Самостійна робота учнів з математики в навчальному процесі початкової школи

Тепер освіта зорієнтована на індивідуальний розвиток особистості, тому вчитель повинен цілеспрямовано формувати в учнів здібності до самореалізації і саморозвитку, цілеспрямовано формувати і розвивати окремі якості учня, які допоможуть йому "знайти себе" і реалізувати свій потенціал. А процес учіння має сьогодні розумітися як знання, сприйматися як переконання, втілюватися як дія.

Вважаємо, що одне з головних завдань сучасної математики - навчити учнів самостійно працювати, оскільки темпи надходження наукової інформації зросли і практично кожній людині, яка хоче мати роботу та продуктивно працювати, необхідно увесь час оновлювати свої знання, а то й переучуватись, а це можливо лише за наявності в неї умінь і навичок самостійної роботи.

Організовуючи самостійну роботу на уроці на формувальному етапі експерименту керувалися такими дидактичними вимогами:

1. Організовувати самостійну роботу на всіх ланках навчального процесу, у тому числі й під час засвоєння нового матеріалу. Необхідно забезпечити оволодіння учнями не тільки знаннями, а й загальними уміннями, засобами розумової праці, за допомогою яких засвоюються знання.

2. Завдання самостійної роботи повинні бути спрямовані не стільки на засвоєння окремих фактів, скільки на розв'язування різноманітних проблем. У самостійній роботі треба навчити учнів бачити і формулювати проблеми, самостійно вирішувати їх, вибірково використовуючи для цього наявні знання, уміння і навички, перевіряти отримані результати.

3. Для активізації розумової діяльності учнів треба давати їм роботу, що вимагає посильного розумового напруження.

Самостійну роботу залежно від її мети проводили на різних етапах уроку (закріплення, повторення, ознайомлення з новим матеріалом).

Плануючи завдання для самостійної роботи врахували можливості кожного виду роботи і відповідність мети уроку. Тому використовуючи картки з диференційованими завданнями, план опрацювання нового матеріалу, ми застосовували інструкції, підказки, "ключик" для розв'язання, використовували самостійні роботи з наперед заготовленими відповідями. Старалися, щоб підказки були гранично чіткими й лаконічними, вимагали, щоб учні робили висновки після виконання кожного виду самостійної роботи.

Пропонували 5-6 хв. самостійні роботи з метою первинного закріплення, з метою перевірити наскільки учні зрозуміли новий матеріал і виявити помилки. На цьому етапі роботи важливо швидко зорієнтуватися, чому учень помиляється (не зрозумів пояснення, не знає попереднього матеріалу, через неуважність, тощо).

Такі самостійні роботи допомагали утворити диференційовані підгрупи учнів, використовуючи адаптовані до їх можливостей навчальні матеріали, впроваджуючи принцип вільного вибору варіантів завдань, що відповідають можливостям і підготовленості учнів.

Особливу увагу звертали на роботу з учнями, які виконують індивідуальні завдання вищого рівня складності. Якщо при виконанні завдання такі учні відчували трудність, то надавали інструкцію щодо розв'язання, але поетапно. Зважали на те, щоб ця інструкція була лаконічною, але достатньою і точною. Її зміст відображав послідовний хід міркувань, практичних дій, що приводять до засвоєння нового поняття і т.д.

Форму самостійних завдань урізноманітнювали, щоб працювали різні види сприйняття і пам'яті: зорова, слухова, моторна. Досить часто при вивченні теми пропонували змоделювати описану усно ситуацію за допомогою моделей прямих, площин, пропонували зробити висновок і перевірити його із сформульованим висновком у підручнику і т.д.

Результативність самостійної роботи залежить і від того, як вчитель зуміє поєднати способи виконання завдань: усні з письмовими, фронтальні з індивідуальними.

З одного боку, ефективність самостійної роботи учнів залежить від підготовленості вчителя до її організації, тобто його вміння здійснювати діагностику індивідуальних реальних можливостей учнів, аналізувати зміст навчального матеріалу і визначати характер можливих труднощів для засвоєння його учнями, розробляти систему завдань для самостійної роботи учнів, надавати їм консультативну допомогу.

З іншого боку, вона залежить від підготовленості учнів до самостійної роботи, від їхнього ставлення до неї та володіння необхідним запасом знань з математики, вміння аналізувати і структурувати навчальний матеріал з метою його осмислення [28].

Будь-яка робота дає позитивні результати тільки тоді, коли вона є системною, що задовольняє певні вимоги.

Організовуючи самостійну роботу дотримувались певних основних вимог.

1.Самостійна навчально-пізнавальна діяльність повинна:

а) допомагати учням засвоювати математику глибоко і міцно;

б) розвивати їх пізнавальні здібності;

в) формувати вміння самостійно розширювати і поглиблювати знання та застосовувати їх на практиці;

г) відповідати основним принципам дидактики; а саме доступності, систематичності, зв'язку теорії з практикою, свідомості, творчої активності, навчанню на високому рівні.

2. Завдання, що входять до системи самостійної діяльності, мають бути різними з дидактичною метою та змістом.

3. Послідовність виконання домашніх і класних самостійних робіт повинна бути такою, щоб виконання одних робіт логічно випливало з попередніх і підготовляло учнів до виконання наступних.

4. Самостійна робота повинна носити цілеспрямований характер, що досягається чітким визначенням її мети; недооцінення цієї вимоги приводить до того, що учні неправильно виконують завдання, або вимагають від учителя додаткових пояснень, через що відбувається нераціональне використання часу.

5. Самостійна робота має бути дійсно самостійною, а її зміст та обсяг-посильним для учнів на даному етапі.

6. Спочатку в учнів необхідно сформувати елементарні навички самостійної діяльності, як під час роботи з підручником, так і при виконанні практичних завдань, малюнків, простих вимірів, розв'язуванню задач. Цьому повинна передувати наочна демонстрація учителем цих видів роботи, яка супроводжується чіткими поясненнями і записами на дошці.

7. Для самостійної роботи учням необхідно пропонувати завдання, що розв'язуються за готовими алгоритмами, а також і такі, які вимагають їх створення.

8. Необхідно враховувати те, що різним учням потрібна різна кількість часу для засвоєння одних і тих самих знань, умінь та навичок.

Завдання мають бути цікавими для учнів.

10. Надмірне захоплення самостійною роботою учнів може сповільнити темп навчання.

11. Учитель визначає мету, зміст, обсяг, методи і види самостійної роботи.

Ефективність самостійної роботи збільшується, якщо вона є однією зі складових навчального процесу і проводиться планомірно та систематично, якщо на кожному уроці для неї відводиться певний час. Тільки за таких умов у учнів формуються стійкі вміння та навички щодо виконання різних видів самостійної роботи.

Використовували в експериментальній роботі систему диференційованих завдань, що складалися з:

1. Триваріантних завдань за ступенем складності (полегшеної, середньої, підвищеної) при цьому варіант вибирає учень.

2. Спільного для всього класу завдання із системою додаткових завдань, ступінь складності яких зростає.

3. Індивідуальних диференційованих завдань.

4. Групових диференційованих завдань з урахуванням різної підготовки учнів (варіант визначаю сама).

5. Рівноцінних двоваріантних завдань, до кожного з яких додаються завдання зростаючої складності.

6. Спільного практичного завдання із зазначенням мінімальної і максимальної кількості задач або прикладів для обов'язкового виконання.

Індивідуально-групових завдань.

Учнів кожного класу (групи) умовно поділили на три групи:

"А" - учні, які потребують допомоги, вони мають невисокий рівень розвитку здібностей і мислення, тому навчання відбувається через наочний матеріал;

"Б" - учні, які можуть засвоїти матеріал у рамках програми, робота з ними потребує постійного вивчення мотивації навчальної діяльності;

"В" - учні з високим рівнем математичних здібностей, завдання для них підбираються не тільки за ступенем складності, а й за індивідуальними особливостями.

Отже, за допомогою самостійної роботи прагнули розвивати здібності кожного, організувати навчання так, щоб добре підготовлені учні мали можливість виконувати складніші завдання, учитися швидше, а недостатньо підготовлені виконували менш складні завдання, але поступово підвищували свій рівень знань. Виконання складнішого варіанта завдань стає метою кожного учня. Діти мають можливість ознайомитися з виконанням тих завдань, які на даному уроці були їм не під силу. З цією метою наприкінці уроку я відводжу час на їх пояснення. Для тих учнів, які на уроці виконували полегшені завдання, додому задається завдання другої групи складності; для тих, хто впорався з роботою другого ступеня, домашнім завданням є завдання більш високого ступеня складності. Надавали можливості учням вибирати завдання домашньої роботи самостійно.

Учні, які добре володіють навичками самостійної роботи належно працюють в групі на етапі початкового сприйняття нового матеріалу, що особливо важливо у старших класах при організації лекційно-семінарських занять.

Ефективність уроку залежить і від того, як вчитель вміє реалізувати розвивальні цілі уроку. Тому готуючись до кожного уроку передбачали розвивальні ситуації, а саме:

а) розучували здобувати знання самостійно, при цьому організовуючи і направляючи сам процес учіння;

б) спочатку добре продумували, а потім ставлю запитання так, щоб вони активізували самостійну думку учня;

в) формували в учнів інтерес до навчання через проблемно-пошуковий підхід до висвітлення теми, через цікаві завдання.

На етапі уроку “Контроль, корекція та оцінювання знань” потрібно вчити дітей здійснювати самоконтроль, самоаналіз і самооцінювання. (Фрагменти уроків представлено в додатку 1)

Використовуємо групову і парну форму взаємоконтролю і взаємоаналізу, рефлексивного аналізу і контролю. Звертаюся до таблиць “Повинні знати”, “Повинні вміти”, до планування уроку та перевірки, чи все заплановане вдалося зробити, чи всі завдання уроку виконані.

Таке моделювання уроку можливе тільки при комбінуванні різних методів і прийомів навчання. А це відкриває шлях до творчості, дає можливість проводити різні види уроків. Основою їх проведення є цікавий зміст, самостійний вибір, неординарний підхід і інтелектуально-ігрова ситуація. Останньою керую так, щоб вона по можливості, проходила через дві стадії: дослідницько-спостережувальну і комбінаторно-конструктивну. Як наслідок, одразу, як тільки створюються зовнішні ігрові умови, значно підвищується увага та активність дітей. Це дозволяє в легкий спосіб формувати мислительні операції. Ті ж ігрові умови дають змогу алгоритмізувати навчальну діяльність дітей. Вони чудово орієнтуються у логіці завдань, які перед ними ставляться. У правильній послідовності здійснюють аналіз порівняння, абстрагування, часом, і узагальнення [29].

В центрі уваги завжди ставлю проблему інтелектуального розвитку і уміння вчитися.

Готуючи завдання на вибір або завдання для групової роботи, враховуємо рівень складності за індивідуальними можливостями, міру своєї допомоги. Це дає можливість створити умови для розвитку кожної дитини, не допустити відставання слабких дітей і водночас не стримувати темпу зростання сильних учнів.

В своїй роботі керуємся принципами:

1)  Кожній дитині, навіть неслабкій, дати міцні знання.

2)  У кожній дитині бачити неповторну особистість, індивідуальність.

3)  Кожну хвилину перебування дитини в класі перетворювати на радість.

Учні кольоровими картками сигналізують про обраний варіант, що дає можливість побачити кожного учня, визначити рівень допомоги кожному.

Види допомоги такі:

-  доповнення до завдання у вигляді малюнка, схеми;

-  розв`язання аналогічного завдання, виконаного раніше;

-  посилання на правило, на якому базується дана вправа;

-  використання умовних записів, зразків, опорних схем;

-  попередження учнів про типові помилки.

Під час закріплення матеріалу самостійну роботу проводжу за схемою:

І варіант працює так:

основне завдання – самостійно

творче завдання – самостійно

цікаве завдання – самостійно

спільне завдання – самостійно.

ІІ варіант – заходи допомомги (опорні схеми, зразки)

основне завдання – самостійно

творче завдання – самостіно

спільне завдання – самостійно.

ІІІ варіант – з учителем; рівень допомоги (опорні схеми, зразки)

основне завдання – самсостійно

спільне завдання – самостійно.

Велику увагу приділяємо розвитку мовленнєвих умінь, щоб учні на основі нової інформації та власного досвіду вміли формувати свою думку, не сиділи пасивно на уроках, а розмірковували, робили припущення. Коли діти вірять, що їхні думки і те, що вони говорять, думають є важливим, і кожному з них дозволено сказати “Я згоден”, “Я думаю інакше”, тоді вони можуть включатись в процес критичного мислення. Від таких уроків учні отримують задоволення.

Використовуємо групову і парну форму взаємоконтролю і взаємоаналізу, рефлексивного аналізу і контролю. Звертаюся до таблиць “Повинні знати”, “Повинні вміти”, до планування уроку та перевірки, чи все заплановане вдалося зробити, чи всі завдання уроку виконані.

Таке моделювання уроку можливе тільки при комбінуванні різних методів і прийомів навчання. А це відкриває шлях до творчості, дає можливість проводити різні види уроків. Основою їх проведення є цікавий зміст, самостійний вибір, неординарний підхід і інтелектуально-ігрова ситуація. Останньою керую так, щоб вона по можливості, проходила через дві стадії: дослідницько-спостережувальну і комбінаторно-конструктивну. Як наслідок, одразу, як тільки створюються зовнішні ігрові умови, значно підвищується увага та активність дітей. Це дозволяє в легкий спосіб формувати мислительні операції. Ті ж ігрові умови дають змогу алгоритмізувати навчальну діяльність дітей. Вони чудово орієнтуються у логіці завдань, які перед ними ставляться. У правильній послідовності здійснюють аналіз порівняння, абстрагування, часом, і узагальнення [29].

В центрі уваги завжди ставлю проблему інтелектуального розвитку і уміння вчитися.

Готуючи завдання на вибір або завдання для групової роботи, враховую рівень складності за індивідуальними можливостями, міру своєї допомоги. Це дає можливість створити умови для розвитку кожної дитини, не допустити відставання слабких дітей і водночас не стримувати темпу зростання сильних учнів.

За допомогою яких методів вдається реалізувати розвивальні цілі уроку? В своїй роботі користувалися перш за все методом проблемного навчання і формування творчих здібностей учнів. Невід'ємною частиною цього методу є евристична бесіда, під час якої, під керівництвом вчителя, учні проходять весь шлях пошуку нового знання аж до його відкриття, а саме: створювали умови для виникнення проблемної ситуації, спонукали учнів сформулювати проблему, керувалися самим процесом пошуку (ставили допоміжні запитання, стимулювали учнів до спостережень, порівняння, застосування раніше здобутих знань у новій ситуації, контриприклади), спонукали до формування висновку, (а якщо є потреба, коректували висновок). Таку бесіду з учнями проводили за наперед заготовленим і записаним на дошці планом, в якому вказано сторінку у підручнику, абзац, тощо. Отже, учні вчаться самостійно здобувати знання. А всілякі запитання вчителя дають змогу добитися усвідомлення учнями вивченого.

В процесі експерименту доведено, що дитина розвиватиметься, вдумливо працюватиме, збагачуватиме свої пам'ять і фантазію, якщо завдання, які вона виконує на уроках будуть цікавими. Тому пропонували учням вправи, які не потребують додаткових знань, але, маючи пошуково-проблемний характер, вчать порівнювати, аналізувати, співставляти з протиставленням, встановлювати деякі математичні закономірності.

Це задачі із циклу "Стежинкою до математичних узагальнень", "Вчимося і розвиваємося з дідусем Всезнаєм", "Математика з посмішкою" (Додаток 2).

На кожному уроці перед учнями ставили завдання (що вони повинні знати, чому навчитися, якими знаннями володіти). Важливу роль відводимо викладанню програмового матеріалу блоками. На початку вивчення теми проводиться оглядово-установча лекція з елементами бесіди (з планом лекції учні ознайомлюються заздалегідь), під час якої акцентується увага на вузлових питаннях теми, їх взаємозв'язках.

Враховуючи різний темп сприйняття матеріалу учнями, найважливіші питання висвітлюються повторно. Основне завдання просто домогтися, щоб усі учні працювали на уроці, до того ж охоче, із цікавістю, результативно, а створити такі умови навчання, за яких кожен учень міг би працювати на уроці відповідно до рівня загальної підготовленості на сьогоднішній день. Для учня, який не встигає, лише посильне завдання, щоб виконавши його, він побачив позитивну перспективу в навчанні. А тому, хто добре знає навчальний матеріал, пропоную завдання творчого характеру. Привчаємо учнів уважно слухати, спостерігати, набувати навички, робити висновки. Тому пояснення деякого матеріалу пов'язуємо із виконанням практичної роботи, яка, часто допомагає створити проблемну ситуацію, яку учні розв'язують самі або за невеликою допомогою вчителя. Це сприяє кращому розумінню навчального матеріалу. Щоб навчити учнів слухати і чути, заслуховуємо учнівські рецензії на відповіді колег по класу. В рецензії учень дає оцінку теоретичних знань, вказує на недоліки, доповнює відповідь. При проведенні практичної роботи учні вголос коментують спостереження, роблять висновки, записують в зошит досягнуті результати. Практикуємо коментовані вправи, які виробляють увагу, сприяють кращому запам'ятовуванню.

Переслідуємо мету - вчити дітей мислити, жити, а це значить розв'язувати задачі. Звичайно часткові способи розв'язування задачі можна забути, але загальне уміння, загальний підхід має зберегтися у кожної дитини на все життя. Тому надаємо великого значення поясненню задач (зокрема задач на %, спільну роботу за допомогою малюнка, пропонуючи запросити в гості "Художника", який би допоміг розв'язати задачі). Досить часто пропонували учням розв'язати завдання різними способами.

Вважаємо, щоб в дитини формувалося бажання вміти і потреба здобути знання самостійно, її так потрібно розтлумачити, щоб вона хотіла давати відповідь на запитання (в чому педагогові допомагають зроблені одночасно на дошці, кожним в зошиті малюнок, схема, розданий шаблон, макет). Причому, спочатку кожен міркує самостійно, а потім лише тому, кому не вдається допомагаємо скласти схему, намалювати малюнок і т.д. При розв'язанні нової задачі кожен учень самостійно розшукує подібні їй, які вже розв'язувались, і використовує їх як допоміжні. Так виховуюємо вміння звертатися до власного досвіду і залучати його при розв'язуванні, що розвиває самостійність мислення.

В своїй роботі старались індивідуалізувати навчальний процес. П'ятихвилинні тестові завдання, які часто пропонували зразу ж після пояснення нового матеріалу, дозволяли з'ясувати рівень засвоєння учнями нового матеріалу, чітко вказують над чим і з ким потрібно більше працювати індивідуально на наступному уроці і дозволяють позбутися прогалин. Старались, щоб дітям було цікаво на уроках, щоб вони проявили інтерес до процесу учіння. Тому залучали історичні відомості, цікаві задачі, вислови вчених математиків, народну математику (Додаток 3).

Не секрет, що основна маса дітей з року в рік втрачає інтерес до навчання. У розв'язанні цієї проблеми важливого значення надавали використанню диференційованого підходу до навчання, що дає можливість кожному учневі самовиразитись залежно від його розвитку й володіння навчальним матеріалом. Диференційованому підходу до учнів сприяють і додаткові індивідуальні заняття, робота спецкурсів, диференційовані домашні завдання.

Найважливіше у такій співпраці - не обійти увагою жодної дитини, дати кожному висловитись, вчасно підтримати, допомогти, похвалити, заохотити. Щоб учень не зневірився в собі, в своїх силах, слід запропонувати посильне завдання, стежити за рівнем його знань, вчасно перевести на порівняно вищий рівень. Цю проблему диференційованого підходу, психологи розглядають як гуманний підхід до розкриття здібностей учнів. Одним із дійових засобів розвитку творчої особистості є диференційований підхід при розв'язуванні вправ. Вважали, що диференційовані завдання мають різнитися насамперед ступенем самостійності прийомів розумової діяльності, необхідних для їх виконання. В даному випадку завдання можуть містити вказівки щодо прийомів роботи, їх послідовності, а в іншому орієнтуватися на повну самостійність учнів (так, учням, яким важко пропонували при розв'язуванні вправи звернутися до зразка, що є в "Робочому зошиті і т.д.). Проводили диференційованого характеру самостійні роботи, контрольні роботи, також давали домашні завдання диференційованого характеру. А учням, які цікавляться математикою пропонували серію задач на листках, що містять якусь цікавинку, якийсь додатковий матеріал і т.д.

Старалися вкраплювати в тканину своїх занять дидактичні ігри, оскільки "Гра є обов'язковою потребою людини, а особливо молодої" (М.Зарицький). Ці короткочасні ігрові ситуації - це продуктивно-пізнавальні пошукові проблемні завдання, які спонукають мислити, свідомо засвоювати і осмислювати вивчений матеріал, бо при розв'язуванні цих завдань, учнів навчали міркувати і робити висновки згідно правил Яна Амоса Коменського "від відомого до невідомого, від простого до складного, від загального до часткового" (це "Заморочки із срібної бочки", "Стежинкою до математичних узагальнень", задачі-загадки, задачі-жарти, "Слабка ланка" та інші) (Додаток 4,5).

Застосовували метод узагальнення, який залежить від рівня підготовленості до нього учнів. Тому ще до вивчення ними теми повідомляємо контрольні запитання, а перед узагальнюючим уроком даю домашнє завдання, в якому зазначені запитання для повторення і узагальнення матеріалу, необхідні навчальні посібники, інша література.

Для того щоб учні прагнули працювати, а отже і міркувати, вчитель має забезпечити моральну, психологічну атмосферу уроку, а тому, спонукаючи учнів до праці рекомендуюємо: "Спробуй, це тобі сподобається", "Ти добре вмієш це робити", "Спробуй, в тебе все вийде..." і т.д.

Вважаємо, що важливе місце на уроці має бути відведене оцінюванню, яке має бути тривалим, дієвим стимулом активності учнів на уроці, зрозумілим за змістом; вказувати (прямо чи опосередковано) на способи виправлення помилок, нести позитивні емоції, адже за словами В.Сухомлинського "Успіх у навчанні - єдине джерело внутрішніх сил дитини, які породжують енергію для подолання труднощів, бажання вчитися".

Що ж дає така система?

По-перше, допомагає учню повніше виявити свою індивідуальність, позбутися страху перед опитуванням, або важким завданням, відчути інтерес до уроку й навчання в цілому;

По-друге, морально готує учнів до свідомого навчання у вищих навчальних закладах; дає можливість краще засвоїти навчальний матеріал шляхом багаторазового повторення теми чи розділу; забезпечує диференційований підхід до навчання в межах одного класу, і, нарешті, вона забезпечує розвиток від нижчого ступеня знань до більш продуктивного, та до оволодіння міцними знаннями.

Застосування індивідуально-масових форм роботи забезпечує самостійне виконання різних завдань всіма учнями одночасно. Вони інтенсифікують навчальний процес, дають змогу корисно розподілити робочий час.

Крім цього, ці методи ставлять учня віч-на-віч з певною проблемою, вимагають творчого переосмисленого підходу до набутих знань, розвивають мислення.

Зростає й інтерес учителя до таких нестандартних уроків, оскільки вони спонукають до творчості.

Таке раціональне поєднання стандартних і нестандартних форм і методів дало позитивний результат. Мої вихованці проявляють інтерес до математики.

Щодо форм роботи, то надавали перевагу самостійному виконанню навчальних завдань з наступною перевіркою, самоперевіркою, що дозволяє розвивати самостійність мислення, використовуючи власний досвід при розв'язанні, виділяти головне в інформації.

Програму з математики складено так, що через урок пояснення нового матеріалу. Тому перевагу надавали "комбінованим урокам" (Див. Додаток 5), урокам формуванню знань і вмінь та навичок учнів, на яких учні поступово нагромаджують знання, удосконалюють вміння з наступним узагальненням, тобто рухаються від часткового до загального. Систему вивчення цих уроків, намагались спрямувати на поступове засвоєння учнями матеріалу паралельно з удосконаленням знань і навичок постійним контролем, узагальнення вивченого. Особливого значення надавали урокам перевірки оцінки і корекції знань, урокам систематизації і узагальнення, а також підсумковим урокам.

 

ІІ.2 Аналіз результатів дослідження

Завданням контрольного етапу дослідження було виявлення результатів формуючого експерименту і ефективності програми експериментальної роботи. Для цього нами, по-перше, була проведена діагностична робота за визначенням рівня сформованості обчислювальних навичків, досягнутого ними в ході апробації серії уроків. По-друге, був зроблений порівняльний аналіз даних, отриманих в ході дослідницької роботи в контрольному і експериментальному класах на констатуючому і контрольному етапі. Для цього були використані ті ж методи, що і на констатуючому етапі. На початку даної частини дослідження, нами був проведений зріз по виявленню досягнутого рівня математичних навичків.

Для виявлення математичних умінь дітям пропонувалося виконати обчислення, вибрати правильні відповіді зі всіх запропонованих.

Друге завдання ставило своєю метою виявити уміння виявляти помилки вчителя і пояснювати їх появу. Для цього було запропоновано завдання: перевірити обчислення та пояснити хід рішення.

З метою виявлення та реконструювання рішення було запропоновано завдання, направлене на вибір правильного рішення і виправлення невірного:

Результати проведеного зрізу представлені в таблицях. За даними експерименту можна зробити наступні висновки: вибрати правильні відповіді зі всіх запропонованих змогли все учні. Подібні завдання виконувалися дітьми на формуючому етапі експерименту і викликали у них великий інтерес.

 Виявити помилки вчителя змогли 95,6% учнів. Василишин К. не справився із завданням у зв'язку з відсутністю на багатьох заняттях формувального експерименту. В ході індивідуальної бесіди, яка була проведена з кожним учнем, Грицюк. А., Топірців. Ю., Торгашин. У. не змогли пояснити причину появи помилки.

Наступне завдання, метою якого було уміння здійснювати післяопераційний і рефлексія контроль, виявилося складним для учнів. Реконструювали рішення тільки 69,5% (16 чоловік). Андрійчук З; Лісицький. І; Ольховський. Э ; Торгашин. У. не здійснили контроль по процесу.

Більшість дітей обмежилися знаходженням помилки в процесі обчислення, не виконавши контроль рефлексії. Для виявлення відношення дітей до математики, обчислювальних прийомів, нами була проведена бесіда, експериментальні дані якої дозволили отримати наступні результати: 73,9% виконують обчислення із задоволенням. Самостійно виявити помилку здатні 60,8% учнів.

Аналіз даних проведеного зрізу і бесіди дозволили нам виявити рівень сформованості математичних дій експериментального класу.

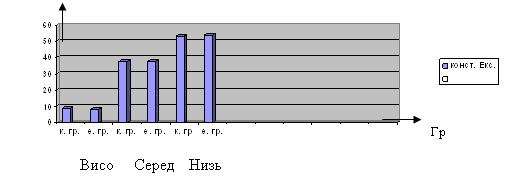
З метою наочного зображення ефективності проведеного формуючого експерименту, представили результати у вигляді діаграми (див. мал. 1):

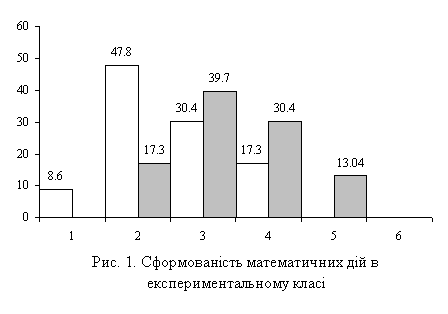
Рівні сформованості математичних дій в контрольному класі представимо наочно (див. мал. 2):

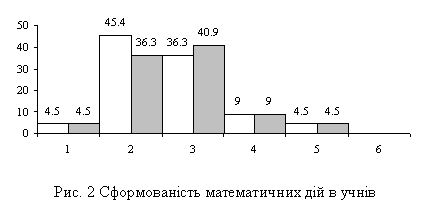
Таким чином, після проведеного формуючого експерименту загальний рівень сформованості математичних дій в експериментальному класі підвищився, а в контрольному класі істотно не змінився.

Аналіз даних проведеного зрізу і індивідуальна бесіда дозволили нам виявити рівні сформованості обчислювальних навиків в експериментальному класі.

Таблиця 3

Сформованість обчислювальних навиків в експериментальному класі

Рівні Критерії	1 людина	2 людина	3 людина
Правильність	0	12	11
Усвідомленість	2	15	6
Міцність	1	12	10

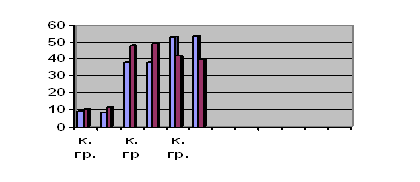
Зобразимо результати (див. рис 3):

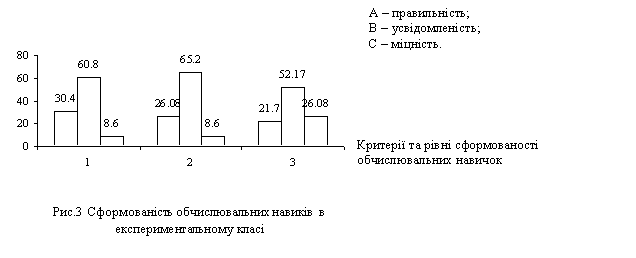
Рівні сформованості обчислювальних навиків в контрольному класі введені в таблицю №4

Таблиця 4

Рівні Критерії	1 людина	2 людина	3 людина
Правильність	5	13	4
Усвідомленість	4	14	4
Міцність	3	15	4

Результати дослідження представлені на гістограмі (див. рис 4)

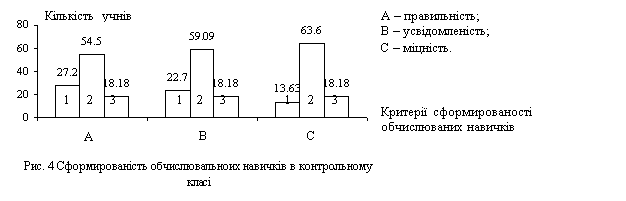
Виходячи з такої обробки даних, отриманих після формуючого експерименту, можна відзначити, що загальний рівень сформованості обчислювальних навичків у учнів контрольного класу практично не змінився, а в учнів експериментального класу підвищився. Отримані результати дають підставу стверджувати про ефективність формуваного експерименту. В цілому можна сказати, що в процесі проведення формувального етапу, у дітей спостерігався інтерес до виконання обчислень самостійно, підвищився інтерес до математики, удосконалилися уміння не тільки виконувати обчислювальні прийоми, але і усвідомлено відноситися до своєї роботи, контролювати дії вчителя, товаришів, уміння міркувати, що зробило позитивний вплив на процес роботи над обчислювальними прийомами і навиками

Висновки

Експериментальна робота дає можливість сформулювати теоретичні висновки і практичні рекомендації щодо організації самостійної роботи учнів початкових класів.

Аналіз психолого-педагогічної літератури засвідчив, що самостійна робота - це сукупність дій учня з предметами у певних умовах, що передбачають відсутність безпосереднього керівництва та допомоги з боку вчителя, з використанням наявних індивідуальних рис особистості для того, щоб отримати продукт, відповідний заданій меті, в результаті чого має бути сформована самостійність як риса особистості учня та засвоєна певна сукупність знань, умінь та навичок.

Широке застосування самостійної роботи учнів на урокахдає змогу успішно розв’язувати багато навчально-виховних завдань:

-  підвищити свідомість і міцність засвоєння знань учнями; виробити в них уміння й навички, яких вимагає навчальна програма;

-  навчити користуватися набутими знаннями і вміннями в житті, в суспільно корисній праці,

-  розвивати в учнів пізнавальні здібності, спостережливість, допитливість. логічне мислення, творчу активність під час засвоєння знань;

-  прищеплювати їм культуру розумової і фізичної праці, вчити їх самостійно продуктивно і з інтересом працювати;

-  готувати учнів до того, щоб вони могли ефективно займатися після закінчення школи.

В роцесі експериментальної роботи доведено, що використання самостійної роботи на уроці робить урок ефективним, бо вона:

1.  формує світогляд, теоретичні знання, практичні і трудові вміння;

2.  2.уміння, навички узагальнювати;

3.  3.систематизувати і застосовувати знання, уміння й навички; вміння вчитися, навички самоосвіти;

4.  закріплення знань, умінь;

5.  розвиває мислення, пізнавальний інтерес, активність, пам'ять, волю, емоції;

6.  .спонукає до продуктивного мислення; застосування набутих знань, умінь; вияву ініціативи; змагання, колективної співпраці.

В процесі роботи доведено, що розроблена програма експериментального навчання є ефективним засобом формування самостійних навичків унавчальної діяльності молодших школярів.

Результати дослідження показали, що із зростанням самостійної роботи на уроці математики посилюється пізнавальний інтерес до уроку математики, удосконалюються обчислювальні навички.

Припущення, висунуте на початку дослідження, в основному підтвердилося: формування основ самостійної роботи учнів при дотриманні наступних умов:

1. Групові роботи не можуть проводитися часто під час вивчення нового матеріалу. Їх можна організувати тоді, коли навчальний матеріал не містить складних теоретичних понять, не вимагає показу демонстраційних дослідів та ін. В умовах спільного повторення ліквідується можливість прогалин у засвоєнні, учні надають один одному допомогу, пояснюють помилки, неточності, спільно обговорюють висновки.

2. Індивідуальна самостінйа робота найчастіше дає позитивні результати, коли учні, знаючи загальні положення, закономірності, можуть зробити окремі висновки про властивості речовин, розв’язати доступні, але досить складні завдання. Однак такі роботи можна організувати не стільки в процесі сприймання нових знань, скільки під час повторення добре усвідомленого матеріалу.

Таким чином, названі вище умови необхідні для успішного застосування методу самостійної роботи на уроках. Вони є основними, найбільш загальними. У процесі навчання можуть створюватись і такі ситуації, коли інші фактори на перший погляд випадкові і незначні, впливають на вибір того чи іншого методу. Тому правильний спосіб проведення уроку та ефективну методику організації самостійної роботи може вибрати вчитель, який знає загальні рекомендації і всебічно оцінює наявні умови.

Список використаних джерел:

 

1.  Абрамова Г. С. Возрастная психология. Учебное пособие для студент. вузов.- М.: Академия, 1997 – 638 с.

2.  Аргинская И. И. Математика 3 класс. – Самара, « Корпорация» Федоров», 1997 – 88 с.

3.  Бабанский Ю. К. Оптимизация процесса обучения. Общедидактический аспект. – М.: Педагогика, 1977 – 254 с.

4.  Берцфаи Л. В., Романко В. Г. Исследование особенностей рефлексивного контроля. Сообщение 1 // Новые исследования в психологии – 1981, - №2 – с. 68 – 72

5.  Бадма – Гаряева М. В. Развитие вычислительных навыков у учащихся 1 класса // Начальная школа – 1999 - №11 – с.21 – 23

6.  Бантова М. А. Система формирования вычислительных навыков // Начальная школа – 1993 - №11 – с. 38 – 43

7.  Бахир В. К. Развивающее обучение // Начальная школа – 1997 - №5 – – 31 с. 26

8.  Буряк В.К. Самостоятельная работа учащихся. – К.: Знание, 1990. – 48 с.

9.  Дубравська Д.М. Основи психології: Навч. посібник. – Львів: Світ, 2001. – 280 с.

10.  Давыдов В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования. – М.: Педагогика, 1986 – 239 с.

11.  Давыдов В. В. Содержание и строение учебной деятельности школьников. – М., 1978 – 321 с.

12.  Давыдов В.В. Теория развивающего обучения. – М.: ИНТОР, 1996 – 544 с.

13.  Давыдов В. В. Что такое учебная деятельность // Начальная школа – 1999 - №7 – с. 12 – 18

14.  .Дичковська. .І.М Основи педагогічної інноватики. Рівне, 2001р

15.   Волкова. Н.П. Педагогіка. Київ, Видавничий центр "Академія",2002р.

16.  Захарова А.В. Развитие контроля и оценки в процессе формирования учебной деятельности//Формирование учебной деятельности школьников. – М., 1982 – 234 с.

17.  Зимняя И. А. Педагогическая психология. – Ростов на Дону: Феникс, 1997 – 476 с.111

18.  Зоренко И.С. Дидактические условия организации самостоятельной учебной работы школьников: Дис… канд. пед. наук. – Кривой Рог, 1997. – 181 с.

19.  Корсакова О. Формування в учнів досвіду творчої діяльності // Шлях освіти. - 1999. - №2. – С. 35-39.

20.   Лозова В.І. Пізнавальна активність школярів. – Харьків: Основа, 1991.

21.  Леонтьев Л. Н. Деятельность. Сознание. Личность – 2 – е изд. – М., 1977 – 364 с.

22.  Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. – 186 с.

23.  . Матеріали газети "Математика"2001р., 2002рр

24.  Махмутов М.И. Вопросы организации проблемного обучения. – Казань: Каз. ГУ, 1971. – 63 с.

25.   Оконь В. Основы проблемного обучения. – М.: Просвещение, 1968. – 208 с.

26.  Особенности психического развития детей 6 – 7 летнего возраста /Под ред. Д.Б.Эльконина, А.Л.Венгера – М.: Педагогика, 1988 – 137 с.

27.  Познавательные процессы и способности в обучении / Под ред. В.Д. Шадрикова. – М.: Просвещение, 1996 – 168 с.

28.  Педагогіка і психологія. Науково-теоретичний та інформаційний журнал академії педагогічних наук України. Київ "Педагогічна думка". №1-2 (34-35)'02р.

29.  .Підласий І.П "Як підготувати ефективний урок" Київ "Радянська школа, 1989р."

30.   Підручна М., Яценко І.. Дидактичні ігри на уроках математики. – К., 1990.

31.  Психологическое развитие младших школьников/ Под ред. В.В. Давыдова. – М.: Педагогика, 1990 – с.22—103

32.  Реализация межпредметных и внутрипредметных связей в обучении и воспитании младших школьников: Межвузовский сборник научных трудов. – Л., 1984 – 132 с.

33.  Репкин В.В. Формирование учебной деятельности в младшем школьном возрасте//Начальная школа – 1999 - №7 – с.19 – 24

34.  Репкина Г.В., Заика Е.В. Оценка уровня сформированности учебной деятельности. Томск: Пеленг, 1993 – 62 с.

35.  Романко В.Г. Особенности рефлексивного контроля как учебного действия//Новые исследования в психологии – 1985, - №1 – с.65 – 71.

36.   Руссо Ж.–Ж. Эмиль или о воспитании: Пер.с франц. М.А. Энгельгардтъ. – С.-Пб.: Изд. газ.”Школа и жизнь”, 1912. – 489 с.

37.  Самоконтроль младших школьников в процессе решения арифметических задач: Методические рекомендации / Сост. Г.М. Соснина. – Иркутск, 1983 – 34с.

38.  Сорока Г.І. Організація колективної творчої діяльності учнів: Методичні рекомендації. – Харків: ХДПУ, 1995. – 41с.

39.   Сухомлинський В.О. Вибрані твори: В 5-ти т. –К.: Рад. школа, 1977. – Т. 4. – 638 с.

40.  Талызина Н.Ф. Педагогическая психология – М.: Академия, 1998 – 497 с.

41.  Талызина Н.Ф. Формирование познавательной деятельности младших школьников. – М.: Просвещение, 1988 – 374 с.

42.  Фридман Л.М., Кулагина М.Ю. Психологический справочник учителя. – М.: Просвещение, 1991 – 287 с.

43.  Філософія: Підручник / За заг. ред. Горлача М.І., Кременя В.Г., Рибалка В.В. К.–Харків: Консум, 2000. – 672 с.

44.  Эльконин Д.Б. Избранные психологические труды. – М., 1995, - 342 с.

45.  Эльконин Д.Б. К проблеме периодизации психического развития в детском возрасте // Вопросы психологии – 1971, - №4 – с. 57 – 61.

Додаток 1

Фрагмент уроку №1

Завдання:

1.  Формувати потребу у здійсненні математичних дій

2.  Розвивати уміння здійснювати контроль по результату;

3.  Розвивати уміння контролювати дії товариша, власні дії;

4.  Розвивати уміння міркувати;

Експериментальні коментарі	Хід уроку
		2 етап – Повторення вид роботи – усний рахунок Завдання для вчителя: перевірити усвідомленість, міцність обчислювальних прийомів щодо усних прийомів складання, ділення. Завдання для учнів: Хлоп'ята, сьогодні ми продовжимо говорити про значення дії контролю, виконаємо завдання, направлені на уміння складати числа, що закінчуються на 0, повторимо усні прийоми ділення;
Уміння здійснювати дії по результатах (зіставляти відповіді) Уміння здійснювати дії по результату. Розвиваємо уміння виявляти помилки в рішеннях товаришів. Це допомагає в розвитку уміння знаходити помилки у власних діях. Розвиваємо уміння доказово міркувати.			Уч. Зад. №1. Практич. Завдання: Знайдіть значення виразів, зіставивши результати і букви на квітках, і ви дізнаєтеся ім'я мультиплікаційного героя, який прийшов до нас на урок. Зміст: 270:270=.; 260:130=.; 930:310=.; 420:105=.; 600:120=.; 666:111=.; 280:40=.; 560:70=.; Хто прийшов в гості? (Степашка). Як ви це дізналися? (Зіставили результати виразів і цифри на квітках). Легіні! Ви дуже кмітливі. Ми перевірили значення виразів за допомогою відповідей. Уч. Зад. №2. Хлоп'ята, хто знає, який птах може ходити по дну водоймища? Щоб відповісти на це питання, виконаєте обчислення: Зміст: 250+150+30+120+250=.; Відповіді: горобець = 850; оляпка= 800; сорока=700; До нас в гості прийшов Незнайко і він стверджує, що по дну водоймища може ходити горобець. Ви з ним згодні? Доведіть, що Незнайко не має рації. Як ви зуміли довести свою правоту? (Виконали перевірку). Як ви вважаєте, без перевірки ви змогли б довести свою думку? Для чого необхідна перевірка? Підсумок: Ми не зможемо довести, що рішення вірне, не будемо упевнені в достовірності результату, якщо не виконаємо перевірку, не проконтролюємо свої дії.

Фрагмент уроку №2

Завдання:

1.  розвивати уміння виконувати математичні дії.

2.  Розвивати уміння ставити уточнюючі питання

3.  Розвивати уміння виявляти помилки в рішеннях товаришів

4.  Розвивати уміння здійснювати контроль рефлексії: реконструювати спосіб дій, що привів до помилки.

5.  Розвивати уміння здійснювати контроль по результату.

Експериментальні коментарі.

Хід уроку

Розвиваємо уміння виконувати математичні дії. Розвиваємо уміння виявляти помилки. Розвиваємо уміння здійснювати контроль рефлексії: реконструювати рішення, що привели до помилки. Розвиваємо уміння міркувати. Розвиваємо уміння розвивати контроль по результату, контролювати дію своїх товаришів.

2 етап. Повторення вид роботи – усний рахунок Завдання для вчителя: перевірити усні прийоми множення і ділення на однозначні, круглі двозначні і тризначні числа. Завдання для учнів: Ми повторимо усні прийоми множення і ділення, продовжимо вчитися виявляти помилки в обчисленнях. Це уміння допоможе нам не припускатися помилки і вчасно помічати їх. Уч. Зад.№1 . Хлоп'ята, Чебурашка і Шапокляк прислали нам декілька виразів. Але в конверті всі вирази переплуталися і тепер ми не знаємо, де рішення Чебурашки, а де «пастки» Шапокляк. Тому ми не можемо бути упевнені, що всі рішення вірні, оскільки Шапокляк любить робити дрібні капості. Наше завдання обговорити вирази і їх значення і виявити помилки, якщо такі є. Зміст: 560:70=80; 360:9=50; 490:90=90; 70 * 9=6500; 30 * 800=2700; 500 * 70=35000; Працюємо в парах. Вам необхідно проглянути всі дії, виявити помилки, пояснити їх своєму сусідові і, доказово міркуючи виправити їх. Отже, скільки обчислень прислав Чебурашка? (Одне). Ви змогли виявити і усунути «пастки» Шапокляк? Легіні! Це допоможе нам не припускатися помилки і бути уважнішими. Уч. Зад. №2 Практіч. Завдання: Знайдіть значення виразів: Зміст: 7080:20=.; 1020:20=.; 630:30=.; 3050:50=.; 2800:40=.; Відповіді для самоконтролю: 308;354;402; 413; 423;484;554; Для того, щоб перевірити себе, підсумовуйте відповіді 1 і 2 виразів. Якщо сума вказана у відповідях для самоконтролю, то значення вірні, переходите до наступного обчислення. Саша назве значення 1 і 2 виразів, їх суму, а ви уважно слухайте і виправляйте з потреби свого товариша. Отже, ми знайшли вірні значення, повчилися контролювати себе, своїх товаришів, виправляти, доказово міркуючи.

Фрагмент урока№3

1.  Розвивати уміння розробляти алгоритм контрольної дії.

2.  Розвивати уміння здійснювати післяопераційний контроль.

3.  Розвивати уміння виявляти помилку в ході обчислень.

Експериментальні коментарі	Хід уроку
Операційний контроль Уміння виявляти помилки в обчисленнях, пояснювати їх. Уміння розробляти алгоритм контрольної дії. Уміння контролювати дії своїх товаришів.		3 етап: Закріплення вивченого матеріалу. Вид роботи – виконання обчислення Завдання для вчителя: закріплювати уміння виконувати письмове ділення багатозначних чисел, продовжити учити виявляти помилки в обчисленнях; Завдання для учнів: Ми продовжимо виконувати письмове ділення багатозначних чисел, повчимося виявляти помилки, пояснювати їх.  Практіч. Завдання: Зла чаклунка Гогера відправила до нас своїх злих слуг мавп. Вони принесли вираз, в якому, можливо, є помилка. Чаклунка упевнена, що ми помилку не знайдемо і перетворимося на дурних учнів. Що нам допоможе знайти помилку? (Перевірка). Правильно, ми повинні повчитися перевіряти не тільки результат рішення, але і важ процес виконання обчислення. Нам необхідно скласти алгоритм перевірки, за допомогою якого ми знайдемо помилку. Ми вже складали подібні алгоритми, так що думаю, ми справимося з цим. Що нам було важливо контролювати в процесі виконання обчислень? На що потрібно звернути увагу? (1. Щоб визначити, правильно ми виділили 1 неповне ділиме, нам необхідно відлічити таку кількість цифр ділимому, скільки в дільнику. Якщо число, що вийшло в ділимому, менше дільника, означає 1 неповне ділиме буде більше дільника на одну цифру. Якщо число, що вийшло в ділимому, більше дільника, отже, воно є 1 неповним дільником. 2. Щоб визначить, чи вірно ми підібрали кількість цифр в приватному, важливо знайти 1 неповне ділиме і порахувати кількість розрядів, що залишилися. 3. Щоб визначити, чи правильно підібрана цифра в приватному, потрібно її помножити на дільника. Число, що вийшло, повинне бути не більше за ділиме, а залишок менше дільника. Ваня спробує поміркувати. Інші уважно слухають і контролюють хід думок свого товариша. Отже, ми справилися із завданням, склали алгоритм перевірки ділення багатозначних чисел, який допоміг нам знайти помилку. Керуючись цим алгоритмом, ви зможете виконувати ділення чисел без помилок.

Додаток 2

 

Хвилини цікавої математики

 

Хвилини цікавої математики проводяться епізодично. Вони можуть плануватися вчителем в зв’язку з поставленою метою, наприклад, викликатив дітей інтерес до організації самостійної роботи. Приведемо подібні запитання, задачі, завдання, які можна запропонувати учням в відповідні періоди їх навчання.

Діти люблять незвичайні задачі в віршах. Тому в звичну для цьогохвилину вчитель може почати бесіду так: “Діти, ви знаєте віршС.Я.Маршака “Багаж”? Звичайно серед дітей знайдуться такі, які знають його напамять. Після цього запропонувати прочитати його хором. А потім сказати:”Теперпослухайте задачу:

Дама здавала в багаж;

Диван, чемодан, саквояж,

Картинку, корзинку, картонку

І маленьку сабачонку.

Але тільки пролунав дзвінок,

Втікло з вагона щеня.

Діти, порахуйте швидше,

Скільки залишилось речей?

З цікавістю діти беруться відгадувати прості ребуси. При цьому необхідно запропонувати не будь – які ребуси, а тільки ті, які мають, визначений зв’язок з математикою: або в його зображенні зустрічаютьсяматематичні знаки, або в відповідях утримується математичний термін, абомає місце першої і другої ознаки одночасно. Ребуси можна раніше зобразити на аркушах паперу. Тоді в любий час вчитель може запропонувати дітям їх для відгадування. Наприклад, вчитель каже: “ Діти, відгадайте, які слова тут написані за допомогою букв та інших знаків:

Ребуси.

1. Баро - барометр

2. сви 100 к - свисток

3. ли 100 к - листок

4. ті 100 - тісто

5. чада - задача

6. А - Куба

7. Е 100 нія - Естонія

8. 100 ляр - столяр

9. 40 а - сорока

10. ш 3 х - штрих

11. с 3 ж - стриж

12. Пі2л

13. 7я

14 мі100

15.100лиця.

Додаток 3

 

Загадки

 

1. Одна нога і шапка, а голови нема. Що це таке? (Гриб.).

2. Штучка – одноручка, носик стальний, а хвостик лляний. Що це?

(Голка).

3. Під двома дугами два яблука з кругами. Що це? (Брови і очі).

4. Коли сухо – клинок, коли мокро – блинець. Одна нога і та без чобота. Що це? (Парасолька).

5. Дві вони кленові, підошви – двохметрові. На них поставиш дві ноги –і по глибокому снігу біжи. (Лижі).

6. Біля ялинок із голок лютневим днем побудовано дім. За травою не видно його, а жильців у ньому мільйон. (Мурашник).

7. Під дахом чотири ноги, на даху суп та ложки. Що це таке? (Стіл).

8. Два брошка, чотири вушка. Що це таке? (Подушка).

9. Шестинога на стелі, а восьминогий жде її в кутку. Що це? (Муха і павук).

10. П’ять хатин, а хід один? Що це? (Рукавичка).

11. Шість ніг без копит, ходить, та не стукає, літає, а не птах, може вверх ногами сидіти. (Муха).

12. Чотири ноги, сто голок несе, а шити не уміє. (Їжачок).

13. Син мого батька, а мені не брат. Хто це? (Я сам).

14. Сімдесят одежинок та всі без застібок. (Капуста).

15. Є, діти, у мене два срібних коня. Їду зразу ж на обох! Що за коні у мене? (Коньки).

16. Хто за рік чотири рази перевдягається? (Земля).

17. Сидить баба у сто шуб вдягнута. Хто її роздягає, той сльози проливає. (Цибуля).

18. Цей кінь не їсть вівса, замість ніг – два колеса. Садись верхи і мчись на нім, - тільки краще управляй рулем! (Велосипед).

19. Дім без вікон та дверей, як зелений сундучок,

В ньому 6 кругленьких діточок.

Називається... ( стручок)

20. Що це за 7 братів: роками рівні, іменами різні. (дні неділі)

21. Росте 4 берези. На кожній березі по 4 гілки. На кожній гілці є по 4 яблука. Скільки всього яблук? ( На березі яблука не ростуть)

22 4 мишки гризли скоринку сиру. Підкралась кішка і схопила 1 мишку. Скільки мишок продовжувало гризти скоринку сиру? ( Ніскільки, всі миші порозбігалися)

Додаток 4

 

Ігри

“Арифметичний квач”.

Беручи участь в грі, діти закріплюють в памятісклад числа 10. гра заключається в наступному. Діти становляться в коло.Один учень є ведучим і становиться в центрі кола. У дітей, які стоять до кола, прикріплені картки з числами від 0 до 10. це в тому випадку, коликрім ведучого, беруть участь в грі ще 11 чоловік. Потім учень – ведучийголосно називає число, наприклад8. тоді учень який стоїть в колі і має число 8 , оббігає коло, щоб доторкнутися до учня з числом 2, яке доповнює 8 до 10. щоб не дати, коли його “заквачують”, учень з 2 повинен швидко здогадатися, що доповнення до 10 число знаходиться в нього, оббігти коло в ту саму сторону, що і 8 і стати на своє місце. Якщо 8 не “ заквачує” 2, то учень з 8 становиться в коло, а минулий ведучий найого місце. При цьому минулий ведучий одночасно отримує від нового ведучого і картку з числом 8 , прикріплює до себе на грудях. Якщо 8 “заквачила” 2 , то учень з числом 2 становиться ведучим, віддаючи свою картку минулому ведучому.

Примітка 1: Якщо ведучий скаже голосно число 10, то, крім учня,який має на картці число 10, повинен оббігати коло і учень з числом 0.

Примітка 2: Якщо учнів, які приймають участь в грі, менше 12, тозвичайно не беруться числа 10, 9, 8 і т. д. І доповнення проводиться донайбільшого з прикріплених на картках чисел. Наприклад, в грі разом зведучим беруть участь 9 чоловік. Тому в колі будуть стояти 8 учнів зприкріпленими числами від 0 до7. в процесі гри доповнення проводиться до числа 7.

Примітка 3: Якщо граючих виявилося більше 12, то доповнення можна вичислити і до більшого числа. Якщо, наприклад, граючих 15, то доповнюють до числа 14.

Гра “Знай таблицю множення”.

Зміст гри наступний. Учасники стають в одну шеренгу. До грудей кожного з них прикріпляються номера від 1 до 9 (послідовно, разом з ведучим в грі можуть приймати участь 10 чоловік). Ведучий називає будь – яке утворення з таблиці множення, наприклад 35. число 35 утворилось від множення 5 і 7 . отже, з шеренги повинні вибігти ті діти, у яких приколені номера 5і 7 , і, добігши до раніш вказаного місця, повернутися в шеренгу. Хто скоріше повернеться на своє місце, то виграє. Він отримує прапорець. Якщо ведучий сказав таке число, яке є добутком двох різних пар чисел ( наприклад, 24 = 6* 4 та 24 = 8*3 ), то з шеренги вибігають всі четверо. Учень, який виграв першим 2 прапорця, становиться ведучим, а ведучий займає його місце. Потім ведучого змінює наступний, отримавши 2 або 3 прапорця. Всі учні, які отримали прапорці, вважаються гарно знаючими таблицю множення.

Гра “Кінцівки”

В процесі цієї гри діти вправляються у виконанні безпосередніх висновків з суджень з відношеннями. Вона корисна тим, що готує дітей до свідомого рішення задач на збільшення і зменшення числа на декілька одиниць і в декілька разів, даних в непрямій формі. Приведемо приклади проведення цієї гри.В неї можуть брати участь 3, 4 і більше учнів. Діти становляться в коло. Я буду починати речення, а ви повинні його правильно закінчити. Закінчувати речення повинен той, докого я доторкнуся рукою. Якщо “кінцівка” учня опиниться не вірною, товін виходить з кола, а хто залишився в колі стараються вірно закінчити речення. Виграють ті, хто вірно давав “кінцівки” і залишився в колі.”Вчитель: “Починаю речення: “Якщо підвіконня вище стола, то...”

Учень: “... то стіл нижче підвіконня”.

Далі речення можуть бути наступними:

- Якщо Саша по росту рівний Петру, то Петро...(по росту рівний Саші)

- Якщо Катя стоїть лівіше Тані, то Таня...( стоїть правіше Каті)

- Якщо в мене в правій руці рахівних паличок на 2 більше чим в лівій,

то в лівій руці...( паличок на 2 менше чим в правій)

- Якщо Марія живе від школи дальше ніж Ніна, то Ніна...(живе від школиближче ніж Марія)

- Якщо сестра старша ніж брат, то брат...( молодший ніж сестра)

- Якщо олівець коротший лінійки, то лінійка...(довша олівця)

Гра “Один, два, не зіб’юсь”

Виходять учасники. По черзі рахують, починаючи з 1, а замість числа, кратного 3 , говорять “не зіб’юсь”. Переможцем буде той, хто назве більше натуральне число. Наприклад: один, два не зіб’юсь, чотири, п’ять,не зіб’юсь, сім, вісім, не зіб’юсь...).

Гра “Виграй приз”.

Потрібно із зав’язаними очима зрізати приз. Якщо учасник, якийзрізав приз, дасть правильну відповідь на математичне запитання,прив’язане до цього призу, він забирає цей приз.

Гра “Весела рибалка”

На підлозі класу обводять контури озера, в яке поміщають рибок.До рибки скріпкою прикріплюються завдання. Учасник бере вудочку. (Накінці ліски – магніт). І ловить рибку. Давши правильну відповідь на запитання – забирає рибку.

Гра “Хто швидше порахує до 25”

На дошці дві однакові таблиці з числами від 1 до 25. хто з

учнів першим закінчить рахунок, той переміг.

Гра “Не зіб’юсь”.

Капітани по черзі роблять по 10 кроків і на кожному кроці

називають:

- приклади на додавання;

- приклади на віднімання.

Гра “Футбол”.

На дошці намальовані футбольні ворота, м’ячі з прикладами. Роль воротаря виконує певна цифра. Суддя – учень з кращих обчислювачів. Діти обчислюють приклади на м’ячиках. Якщо вибрали такий приклад, щовідповідь співпадає з цифрою – воротарем, гол вважається забитим.

Гра “Хто чим пообідає?”

Зайчик із різними цифрами: перед ним малюнки капусти, моркви,буряків, яблук із написаними прикладами. Знайти відповіді до прикладів.

 

Вікторина – блискавка

1. Назвіть три дні підряд, не називаючи днів тижня, чисел. (Відповідь: вчора, сьогодні, завтра ).

2. летіла стая гусей: два попереду, один позаду, два позаду, один попереду. Скільки було гусей?

3. горіло п’ять свічок, три потухло. Скільки залишилось свічок?

4. на гілці сиділо вісім горобців, потім прилетіло ще чотири, а полетіло шість. Скільки стало горобців?

5. скільки років Кості, якщо до його років ще додати вісім і ще один, то буде одинадцять років.

6. Як у кімнаті можна поставити два стільці, щоб біля кожної стіни стояло по одному стільці.

7. колоду завдовжки 5 м потрібно розпиляти на поліна завдовжки 1 м. Скільки треба зробити розрізів?

Додаток 5

 

Цікаві запитання і задачі – смикали

1. а) Скільки одержимо, якщо додамо найбільше однозначне число з найменшим однозначним натуральним числом?

б) Скільки одержимо, якщо додамо найбільше двозначне число і найменше однозначне число?

2. На скільки одиниць більше найбільше двохзначне число, чим більше однозначне число?

3. а) В рамках двадцяти назвати число, в якому число одиниць на 7 більше, ніж його десятків. (Відповідь: 18).

Б) Написати двохзначне число, в якому число десятків на 9 більше числа одиниць. (Відповідь: 90).

4. Використовуючи 2 картки з цифрами 1 і 7, виразити найбільше і найменше двохзначне число. (Відповідь: 17 і 71).

5. Я провів у бабусі понеділок, вівторок, середу і четвер, а моя сестра в цю ж неділю – середу, четвер, п’ятницю і суботу. Скільки всього днів ми гостювали у бабусі? (Відповідь: 6 днів).

6. Як скласти два квадрати із 7 однакових паличок?

7. Мама купила мені 4 стрічки червоного і блакитного кольору. Червонихстрічок було більше ніж блакитних. Скільки стрічок кожного кольорукупила мама?

8. У літні канікули Сергійко побував в Києві, Москві, Каневі, а йогосестра Оленка – в Москві, Каневі, Львові. В яких містах побували діти? Вяких містах були і Сергійко і Оленка?

9. Яке найменше число однакових паличок потрібно взяти, щоб задопомогою їх скласти 3 квадрати? (Відповідь: 10 паличок.).

10. В нашому класі всього 42 учнівських міста. Спочатку навчальногороку у нас було 19 хлопчиків і 18 дівчаток, а потім до нас прийшли ще 4 дівчинки. Чи вистачить учнівських міст для всіх учнів нашого класу?

11. Складіть за умовою задачі вираз і знайдіть його значення: Петя нижчий Колі на 19 см , а Коля вищий Виті на 11 см. Зріст Виті 132 см.Який зріст Петі?

12. Як з допомогою 5 одиниць і одного знаку дії написати число 100? (Відповідь: 111-11=100.).

Задачі-жарти

1. На столі лежали 3 цукерки в одній кучці. Дві матері, дві дочки та бабуся з внучкою взяли цукерки по одній штучці, і не стало цієї кучки.

Як це розуміти. Скільки чоловік брали цукерки?

2. Перед вами стоять в ряду 6 склянок, з яких перші 3 з водою, а решта 3 пусті. Що потрібно зробити, щоб склянки пусті і з водою чергувались між собою при умові, що із всіх склянок можна брати лише 1 і всього 1 раз? (Відповідь: взяти другу склянку, перелити з неї воду у п’яту і поставити на місце.).

3. Два чоловіки підійшли до річки. Біля пустого берегу стояв човен, вякому міг поміститися тільки один чоловік. Обидва без всякої допомоги переправилися на цьому човні через річку і продовжили свій шлях. Як вони це зробили? (Відповідь: двоє підійшли до різних берегів річки.).

4. Два батьки і два сини зїли 3 апельсина. По скільки зїв кожний з них?

(Відповідь: по одному.).

5. В клітці знаходилося 4 кролика. Четверо дітей купили по одному із цих кроликів і один кролик залишився в клітці. Як це могло статися?

(Відповідь: один кролик був куплений з кліткою.).

6. 6 штук картоплин зварилося в каструлі за 30 хвилин. За скільки хвилин зварилась одна штука?

7. У суботу, стомившись від занять у школі і ігор, Костя ліг спати в 9 годин вечора. Щоб не вставати рано ранком, але і не проспати дуже довго,він завів будильник на 11 годин наступного дня. Скільки всього часу вінпроспить, перш ніж розбудить його будильник? (Відповідь: Костя проспитьвсього 2 години, так як в 11 годин вечора того ж дня, тобто в 23 годинибудильник його розбудить.).

8. Скільки кінців у 10 палок? А у десяти з половиною?

9. На березі сиділи дві ворони і дивилися в різні сторони: одна на південь, а друга на північ.

- А у тебе, - говорить перша ворона, - лапки в багні.

-А у тебе, - відповідає друга, - дзьоб у землі.

Як же так? Дивляться в різні сторони, а одна одну бачать?

(Відповідь: вони дивляться одна на одну, а це і є різні сторони.).

10. Що дорожче кілограм гривеників чи півкіло двохгривенників? (Відповідь: кілограм гривеників дорожче чим півкіло двохгривенників, так як вартість металічних монет зв’язана з вагою витраченого на них металу.).

11. Якщо в 12 год. Дня іде дощ, то чи можна ждати через 36 год. Сонячної погоди?

12. Хто назве п’ять днів підряд, не користуючись вказівкою чисел місяця, не називати днів неділі? (Відповідь: позавчора, вчора, сьогодні, завтра, післязавтра.).

Логічні вправи

1. Яка з даних фігур “зайва” (відрізняється від решти)? Чим вона відрізняється?

(Відповідь: третя фігура “зайва”. Вона має 3 сторони, 3 кути, а решта мають по 4 вказані елементи.)

2. Чим відрізняються зображені ряди?

3. Як розрізати фігуру на 2 частини, щоб із них можна було скласти прямокутник?

4. В сумці у мами знаходяться яблука, лимони і апельсини, всього 10 штук. Скільки в сумці окремо яблук, лимонів і апельсинів, якщо кількістьяблук на 7 більше, ніж лимонів? (Відповідь: 8 яблук, 1 лимон, 1 апельсин.).

5. На гілці сиділо 5 синиць і 7 горобців. 6 пташок полетіло. Чи полетів хоча один горобець? (Відповідь: так, полетів, тому що синичок всього, і якщо всі вони полетіли, то тоді серед пташок, які полетіли був горобець.).

6. Що більше – 5 одиниць другого розряду чи 8 одиниць першого розряду?

Додаток 6

Інтегрований урок з математики та природознавства (4 клас)

 

Тема: Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Дії з іменованими числами. Птахи в рідному краї.

Мета. Вправляти учнів у знаходженні значень виразів на сумісні дії з багатоцифровими числами. Удосконалювати вміння учнів розв'язувати задачі на зведення до одиниці. Вчити розв'язувати складні рівняння. Формувати знання про перелітних птахів.

Виховувати бережливе ставлення до природи.

Обладнання: Весняний пейзаж (великого формату); білий папір (великого формату), малюнки перелітних птахів, грамзапис співу пташок, конверти із завданнями.

Хід уроку

Подивіться у вікно. Яка зараз пора року? (Весна). Які ознаки весни ви зараз бачите? На нашу землю прилетіли із теплих країв перші пташки. Послухайте їх радісний спів (грамзапис).Зараз наші пернаті друзі допоможуть нам провести урок і познайомлять нас з частинкою рідного краю, куди вони так спішили прилетіти. Отож сядьте рівненько і послухайте під яким девізом ми будемо сьогодні працювати.

Девіз: Міркуємо – швидко!

Відповідаємо - точно!

Рахуємо – правильно !

Пишемо - гарно!

Усний рахунок: (На окремих листах приклади) Обчислити зручним способом.

4 х 560 х 25 (56000)

15 х 120 х 2 (3600)

500 х 179 х 2 ( 179000)

- А зараз запишіть сьогоднішнє число, класна робота.

- Звертаю вашу увага на правильність написання цифр (на дошці каліграфічно написані цифри).

- Пропоную дібрати з кожного рядка по три доданки так, щоб їх сума дорівнювала виділеному числу - 8600 і записати цифри каліграфічно.

200, 560, 8000, 400, 610 ;

1200, 5000, 2300, 2400, 7600;

- Підкреслити скільки сотень в кожному числі.

( Робота в парах) –Повторити ділення на 10; 100; 1000;

- Дописати каліграфічно ряд, поділивши кожне число на 100.

( 200, 8000, 400; 1200, 5000, 2400; 2, 80,4, 12, 50, 24,)

- Всього на Землі живе 8600 видів птахів, з яких в Україні 360 видів. ( Включаю грамзапис із співом пташок який звучить весь урок, тільки змінюю)

І). А який це птах завітав до нас першим?

Учень: Що за диво, що за птах

Наганяє жабам страх?

На одній нозі дрімає,

На димарі хатку має. (Лелека)

- Першим із птахів на Україну прилітає лелека. Він залетів до нас і приніс конверт. Що ж в цьому конверті? Тут ось яке завдання.

( Робота в парах) Потрібно розв'язати приклад на дошці і виконати самостійну роботу.

26 т 496 кг : 92 (288) - біля дошки

Самостійна робота: (карточки на партах на 2 варіанти)

Ів.

3кг 400г + 2кг 100г =(5кг 500г) - лелека

2кг 90г – 2кг20г = (70г) - шпак

1кг 665г : 37 = (45г) - жайвір

ІІв.

2кг 395г -2кг370г = ( 25г) - соловей

6кг : 60 = (100г ) - зозуля

5кг : 100= ( 50г ) - ластівка

(перевірка фронтально, відповіді в прикладах є відповідна маса птахів, дані прикріпляю біля відповідної перелітної пташки на дошці )

- Ви добре справились із завданням і лелека дозволяє нам відкрити частинку місцевості куди він летить. (відкриваю першу частинку великого білого листа)

2). Після лелек з вирію повертаються шпаки.

(Учень)- Його ми весною зустрічаємо.

У нас він родився і ріс.

Учора з далекого краю

Нам пісню у дзьобі приніс.

- Шпак приніс нам конверт із завданням.

Робота з підручником: №955

( один учень розв'язує біля дошки приклад, коментуючи)

- Другий приклад – коментуючи з місця.

- Шпак відкриває нам другу частину білого листа.

3). До нашого класу влітає ще одна маленька сіренька пташка-жайвір.

( Учень) Жайвір високо у небо літає

Жайвір найперший весну зустрічає.

В нього високий дзвінкий голосочок,

Ніби то срібний б'є молоточок,

Ніби він тягне нитку сріблясту

З неба до лану, людям на щастя.

- Він в конверті приніс нам задачу № 957

(Проводимо аналіз задачі. Розв'язування виконує біля дошки учень)

- Виконавши третє завдання ми можемо відкрити третю частинку білого паперу. Подивіться ще якась пташинка летить до нас.

- (Учень) Відгадайте загадку.

В мене є великий хвіст:

Я співаю як артист.

Спів мій радісний усюди

Дуже люблять слухать люди. (Соловей)

4). З'являється малюнок солов'я і конверт з наступним завданням.

- Пташка пропонує допомогти їй будувати для неї будиночок. Отож візьміть олівець і лінійку. Поставте допоміжну точку. Від неї вправо 3 клітинки і точку А, вправо 6 клітинок – точку В, вниз 8 клітинок – допоміжна точка, вліво 2 клітинки - точка С, вліво 7 клітинок – точка Д. З'єднайте ці точки, дайте характеристику цій геометричній фігурі і знайдіть її периметр. (Один учень коментує роботу з місця, а всі інші виконують.)

- Робота в групах: Накреслені геометричні фігури потрібно розділити на декілька геометричних фігур.

- Виконавши це завдання, ми відкриваємо ще одну частинку листа.

- ФІЗХВИЛИНКА

- Ось іде до нас весна,

- Все навколо ожива:

- Підсніжники прокидаються,

- Проліски посміхаються,

- Діти вибігають,

- На луках стрибають, Птахи прилітають.

5). ( Учень) А можна я загадаю вам ще одну загадку? Я ц ю пташку дуже люблю. Вона влітку живе у нас під дахом.

Швидко скрізь цей птах літає,

Безліч мошок поїдає,

За вікном гніздо будує,

Тільки в нас він не зимує. ( Ластівка)

- В її конверті дуже цікаве завдання. Ластівки живуть біля ваших будинків і нагадують вам , що ви скоро перейдете до 5 класу і повинні вміти розв'язувати складні рівняння.

- ( Рівняння вивішую на дошці)

( 134 + х ) – 583 = 426

- В парах: повторити знаходження компонентів при відніманні і додаванні.(Рівняння розв'язує учень на дошці, коментуючи. Справившись із завданням учень відкриває ще одну частинку білого листа.)

- А що це за пташка давайте відгадаємо.

( Учень) Хто гнізда свого не має,

 Яйця іншим підкладає

Та у лісі в холодку

Все кує „ КУ-КУ, КУ-КУ! ( Зозуля)

- І конверт у цієї пташки незвичайний. Що ж там?

6). ЗУСТРІЧАЙТЕ ВЕСНУ!

(Виходить дівчинка вбрана у весну, відкриває останній білий листок, і розповідає вірш.)

Всі ви добре працювали

На уроці не дрімали,

Гарно руки піднімали

Й знань багато упіймали!

Тож прийміть оці весняні квіти,

Бо ви в класі - працьовиті діти!

(Учениця роздає всім квіти)

Домашнє завдання:

1) Виконати завдання № 960; № 961

2) Прикріпити годівнички для птахів і насипати в них зерна.

Підсумок уроку:

Ось перед нами весняний ліс. Він є домівкою для багатьох тварин. Ми всі повинні берегти цю красу, любити й шанувати рідну природу. Які птахи прилітають до нас найпершими?

Які за масою найважчі? Які найменші? Чому вони до нас прилітають ?

Чи сподобався вам урок? Кому сподобався то поставте свої квіти у вазу біля картини весняної картини.