Навигация
3. Математический анализ
Функция limit – вычисляет предел функции одной переменной
Синтаксис
limit (F, x, a)
limit (F, a)
limit(F)
limit (F, x, a, ’right’)
limit (F, x, a, ’left’)
Описание
Ø Функция limit (F, x, a) определяет предел функции F(x) при x->a.
Ø Функция limit (F, a) автоматически определяет независимую переменную, например t, с помощью функции findsym(F) и затем вычисляется предел функции F(t) при t->a.
Ø Функция limit(F) предполагает по умолчанию в качестве предельной точки a=0.
Ø Функции limit (F, x, a, ’right’) и limit (F, x, a, ’left’) вычисляют соответственно правосторонний и левосторонний пределы.
Примеры.
>>syms x a t h
>>limit (sin(x)/x)
ans=1
>>limit((x‑2)/(x^2–4), 2)
ans=1/4
>>limit((1+2*t/x)^(3*x), x, inf)
ans=exp (6*t)
>>limit (1/x, x, 0,’right’)
ans=inf
>>limit (1/x, x, 0,’left’)
ans=-inf
>>limit((sin (x+h) – sin(x))/h, h, 0)
ans=cos(x)
v=[(1+a/x)^x, exp(-x)]
>>limit (v, x, inf, ’left’)
ans=[exp(a), 0]
Функция diff – выполняет дифференцирование функции одной переменной
Синтаксис
diff(S)
diff (S, ’v’)
diff (S, sym(‘v’))
diff (S, n)
diff (S, ’v’, n)
diff (S, n, ’v’)
Ø Функция diff(S) автоматически определяет независимую переменную с помощью функции findsym(S) и затем выполняет соответствующее дифференцирование.
Ø Функция diff (S, ’v’) и diff (S, sym(‘v’)) дифференцирует символьное выражение S по переменной, указанной в ‘v’.
Ø Функции diff (S, n), diff (S, ’v’, n), diff (S, n, ’v’) дифференцируют n раз символьное выражение S по переменной, указанной в ‘v’.
Ø Если S матрица, то операция дифференцирования применяется к каждому элементу матрицы.
Примеры
>>syms x t
>>diff (sin(x^2))
ans=2*cos (x^2)*x
>>diff (t^6,6)
ans=720
Функция int – выполняет интегрирование функции одной переменной
Синтаксис
R=int(S)
R=int (S, v)
R=int (S, a, b)
R=int (S, v, a, b)
Ø Функция int(S) возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym. Если S – скаляр или матрица, то вычисляется интеграл по переменной ‘x’.
Ø Функция int (S, v) возвращает неопределенный интеграл от S по переменной v.
Ø Функция int (S, a, b) возвращает определенный интеграл от S с пределами интегрирования от a до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
Ø Функция int (S, v, a, b) возвращает определенный интеграл от S по переменной v с пределами интегрирования от a до b.
Примеры
>> x=sym('x');
>> int (x^2, x)
ans =
1/3*x^3
>> int (sin(x)^3, x)
ans =
-1/3*sin(x)^2*cos(x) – 2/3*cos(x)
>> int (log(2*x), x)
ans =
log (2*x)*x-x
>> int((x^2–2)/(x^3–1), x, 1,2)
ans =
– inf
>> int((x^2–2)/(x^3–1), x, 2,5)
ans =
-2/3*log(2)+2/3*log(31)+2/3*3^(1/2)*atan (11/3*3^(1/2)) – 2/3*log(7) – 2/3*3^(1/2)*atan (5/3*3^(1/2))
>> int([x^3 sin(x) exp(x)], x)
ans =
[1/4*x^4, – cos(x), exp(x)]
Функция taylor – служит для получения разложений аналитических функций в ряд Тейлора (и Маклорена)
Синтаксис
taylor(f)
taylor (f, n)
taylor (f, a)
taylor (f, x)
Ø Функция taylor(f) возвращает шесть первых членов ряда Маклорена (ряд Тейлора в точке x=0). В любом разложении можно задавать число членов ряда n, точку a, относительно которой ищется разложение, и переменную x, по которой ищется разложение, например taylor (f, n, x, a).
Ø Функция taylor (f, a) возвращает ряд Тейлора в окрестности точки a.
Ø Функция taylor (f, x) возвращает ряд Тейлора для переменной x, определяемой функцией findsym.
Примеры
>> x=sym('x');
>> F=sin(x);
>> taylor(F)
ans =
x‑1/6*x^3+1/120*x^5
>> taylor (F, 10)
ans =
x‑1/6*x^3+1/120*x^5–1/5040*x^7+1/362880*x^9
>> taylor (exp(x), 1)
ans =
>> taylor (cos(x), – pi/2,6)
ans =
x+1/2*pi‑1/6*(x+1/2*pi)^3+1/120*(x+1/2*pi)^5
Функция yacobian – вычисляет матрицу Якоби
Синтаксис
yacobian (f, v)
Ø Функция yacobian (f, v) возвращает матрицу Якоби для скаляра или вектора f по вектору переменных v. Каждый (i, j) – й элемент матрицы представляет собой частную производную ∂fi/∂vj.
Примеры
>> v=[x, y, z];
>> J=jacobian (F, v)
J =
[2*x, 0, 0]
[1, 1/z, – y/z^2]
[z, 0, x]
>> v=[x; y];
>> J=jacobian (F, v)
J =
[2*x, 0]
[1, 1/z]
[z, 0]
>> J=jacobian (x*y, v)
J =
[y, x]
Функция symsum – вычисляет аналитическое значение суммы ряда
Синтаксис
symsum(S)
symsum (S, v)
symsum (S, a, b)
Ø Функция symsum(S) возвращает символьное значение суммы бесконечного ряда по переменной, найденной автоматически с помощью функции findsym.
Ø Функция symsum (S, v) возвращает сумму бесконечного ряда по переменной v.
Ø Функция symsum (S, a, b) возвращает конечную сумму ряда в пределах номеров слагаемых от a до b.
Примеры
>> x=sym('x');
>> symsum (x^2)
ans =
1/3*x^3–1/2*x^2+1/6*x
>> symsum (1/x^4)
ans =
-1/6*Psi (3, x)
>> symsum (1/x^4,1,5)
ans =
14001361/12960000
>> symsum([x, x^2, x^3], 1,5)
ans =
[15, 55, 225]
Функция solve – решает системы алгебраических уравнений и одиночных уравнений
Синтаксис
solve (expr1, expr2,…, exprN, var1, var2,…, varN)
solve (expr1, expr2,…, exprN)
Ø Функция solve (expr1, expr2,…, exprN, var1, var2,…, varN) возвращает значения переменных varI, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается exprI=0.
Ø Функция solve (expr1, expr2,…, exprN) аналогична предшествующей функции, но переменные, по которым ищется решение, определяются функцией fimdsym.
Примеры
>> syms x y;
>> solve (x^3–1, x)
ans =
[1]
[-1/2+1/2*i*3^(1/2)]
[-1/2–1/2*i*3^(1/2)]
>> solve (x^2‑x‑9, x)
ans =
[1/2+1/2*37^(1/2)]
[1/2–1/2*37^(1/2)]
>> syms a b c;
>> solve (a*x^2+b*x+c)
ans =
[1/2/a*(-b+(b^2–4*a*c)^(1/2))]
[1/2/a*(-b – (b^2–4*a*c)^(1/2))]
>> S=solve ('x+y=3', 'x*y^2=4', x, y)
S =
x: [3x1 sym]
y: [3x1 sym]
>> S.x
ans =
[4]
[1]
[1]
>> S.y
ans =
[-1]
[2]
[2]
>> solve ('sin(x)=0.5', x)
ans =
52359877559829887307710723054658
Функция dsolve – решает дифференциальные уравнения в форме Коши
Синтаксис
dsolve (‘eqn1’, ‘eqn2’,…)
Ø Функция dsolve (‘eqn1’, ‘eqn2’,…) возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqnI.
Примеры
>> dsolve ('D2x=-2*x')
ans =
C1*sin (2^(1/2)*t)+C2*cos (2^(1/2)*t)
>> dsolve ('D2y=-2*x+y', 'y(0)=1', 'x')
ans =
2*x+C1*sinh(x)+cosh(x)
4. Графические возможности
Функция ezplot – строит графики символьно заданной функций
Синтаксис
ezplot(f)
ezplot (f, xmin, xmax)
ezplot (f, [xmin xmax])
ezplot (f, [xmin xmax], fig)
Ø Функция ezplot(f) строит график символьно заданной функции f(x) независимой переменной ‘x’ в интервале [-2*pi 2*pi].
Ø Функции ezplot (f, xmin, xmax) и ezplot (f, [xmin xmax]) позволяют задать диапазон изменения независимой переменной x от xmin до xmax.
Ø Функция ezplot (f, [xmin xmax], fig) обеспечивает спецификацию с помощью параметра fig.
Примеры
>> ezplot ('tan(x)', 0,20)
>> grid on
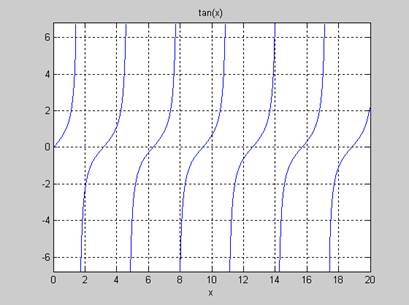
Рис. 1 Графические возможности функции ezplot
Функция ezcontour – строит контурные графики функций вида f (x, y)
Синтаксис
ezcontour(f)
ezcontour (f, domain)
ezcontour(…, n)
Ø Функция ezcontour(f) строит контурный график с настройкой по умолчанию.
Ø Функция ezcontour (f, domain) строит контурный график с заданными параметром domain пределами изменения x и y.
Ø Функция ezcontour(…, n) обеспечивает ранее указанные построения при явном задании числа линий n.
Примеры
>> syms x y
>> ezcontour (sin(x*y), [-3,3], 30)
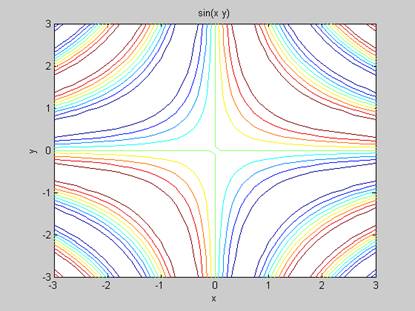
Рис. 2 Графические возможности функции ezcontour
>> syms x y
>> ezcontour (sin(x)*sin(y), [-3,3], 50)
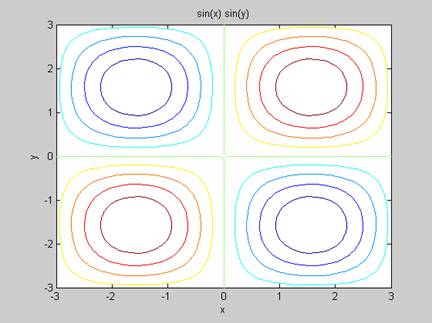
Рис. 3 Графические возможности функции ezcontour
Функция ezplot3 – строит трехмерные графики параметрически заданных функций
ezplot3 (x, y, z)
ezplot3 (x, y, z, [tmin tmax])
ezplot3 (…, ‘animate’)
Ø Функция ezplot3 (x, y, z) строит трехмерный график функции, заданной параметрически уравнениями x(t), y(t), z(t) при настроеке по умолчанию.
Ø Функция ezplot3 (x, y, z, [tmin tmax]) строит трехмерный график функции, заданной параметрически уравнениями x(t), y(t), z(t) при изменениях аргумента t от tmin до tmaxю
Ø Функция ezplot3 (…, ‘animate’) аналогична предшествующим функциям, но обеспечивает анимацию графика.
Примеры
>> syms t;
>> ezplot3 (cos(t), sin(t), t, [0 20], 'animate')
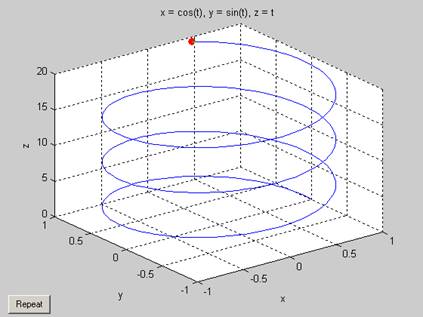
Рис. 4 Графические возможности функции ezplot3
Функция ezsurf – строит графики поверхностей, задаваемых функциями двух переменных f (x, y)
Синтаксис
ezsurf(f)
ezsurf (f, domain)
ezsurf (x, y, z)
ezsurf (x, y, z, [smin, smax, tmin, tmax])
ezsurf (x, y, z, [min max])
ezsurf(…, n)
ezsurf(…, ‘circ’)
Ø Функция ezsurf(f) строит поверхность f (x, y) с параметрами x и y, меняющимися по умолчанию от -2π до 2π.
Ø Функция ezsurf (f, domain) строит поверхность f (x, y) с пределами изменения x и y, заданными параметром domain.
Ø Функция ezsurf (x, y, z) строит поверхность, заданной параметрически зависимостями x (s, t), y (s, t), z (s, t) при s и t, меняющихся в интервале -2π до 2π.
Ø Функция ezsurf (x, y, z, [smin, smax, tmin, tmax]) строит поверхность, заданной параметрически зависимостями x (s, t), y (s, t), z (s, t) при s и t, меняющихся в заданном интервале.
Ø Функция ezsurf (x, y, z, [min max]) строит поверхность, заданной параметрически зависимостями x (s, t), y (s, t), z (s, t) при s и t, меняющихся в одинаковом интервале от min до max.
Ø Функция ezsurf(…, n) аналогична описанным выше командам, но с задаваемым числом линий сетки n.
Функция ezsurf(…, ‘circ’) аналогична описанным выше командам, но вписывает поверхность в окружность
Похожие работы
... наиболее часто используемые при аналитических преобразованиях, располагаются в его системном ядре – части программного обеспечения системы аналитических вычислений, постоянно находящейся в памяти компьютера. К ним относятся команды, выполняющие разнообразные преобразования выражений, получающие решение уравнений и систем уравнений, дифференцирующие функции и т.д. В данной работе вводятся команды, ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
... Windows будем подразумевать операционные системы Windows 95 и Windows NT, имеющие практически идентичный интерфейс пользователя. С точки зрения работы в них системы MathCAD 7. 0 разницы между этими операционными системами нет. 1. 2. Инсталляция и запуск системы Системы MathCAD 7. 0 PRO поставляются на CD-ROM (возможна поставка минимальных версий и на 3, 5-дюймовых дискетах). При этом полная ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...



0 комментариев