Навигация
Проектирование и исследование механизма двигателя внутреннего сгорания
ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ МЕХАНИЗМА ДВИГАТЕЛЯ ВНУТРЕННЕГО СГОРАНИЯ
Пояснительная записка к курсовому проекту
Дисциплина – «Теория машин и механизмов»
Харьков 2009
Введение
Среди рычажных механизмов различных типов одним из наиболее распространенных в технике являются кривошипно-ползунные механизмы (КПМ). Они используются в двигателях внутреннего сгорания (ДВС), компрессорах, насосах, ряде станков (например, прессах) и других машинах различного назначения, включая наземные и воздушные транспортные средства.
Поршневые ДВС служат для преобразования теплоты, выделяющейся при сгорании топлива в цилиндрах, в механическую работу. Механизмы одноцилиндровых ДВС имеют сравнительно небольшую мощность ![]() . Они применяются в основном в энергоустановках для привода в движение электрогенераторов, компрессоров, воздуходувных установок, в самоходных шасси, служат для перемещения грузов и т.д.
. Они применяются в основном в энергоустановках для привода в движение электрогенераторов, компрессоров, воздуходувных установок, в самоходных шасси, служат для перемещения грузов и т.д.
Одним из эффективных средств повышения мощности ДВС является увеличение числа их цилиндров. Поэтому многоцилиндровые ДВС широко распространены в современной технике. В авиации ДВС сейчас применяются в вертолетах, легких транспортных, спортивных и учебных самолетах.
1. Проектирование кривошипно-ползунного механизма ДВС
1.1 Определение линейных размеров звеньев механизма
Проектирование кинематической схемы кривошипно–ползунного механизма (КПМ) заключается в выборе в соответствии с заданными условиями и требованиями значений линейных размеров кривошипа и шатуна.
Определяем ход поршня:
![]() ,
,
где: ![]() – диаметр поршня.
– диаметр поршня.
Запишем ход поршня через длину кривошипа:
![]()
Из отношения длины шатуна к радиусу кривошипа ![]() определим длину шатуна:
определим длину шатуна:
![]()
В качестве начального звена в КПМ выбрано кривошип. Условие существования КПМ:
![]()
1.2 Структурный анализ механизма
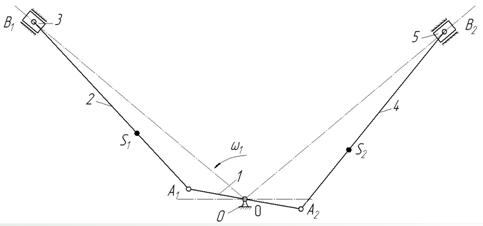
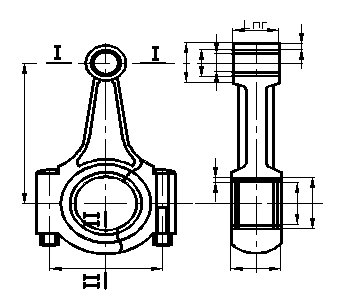
Рисунок 1.2.1. Механизм ДВС – кривошипно-шатунный механизм
1.2.1. Определяем число подвижных звеньев: ![]()
1.2.2. Подсчет и классификация кинематических пар 5 и 4 класса:
1. (0–1) – НКП, вращательная, 5 класса;
2. (1–2) – НКП, вращательная, 5 класса;
3. (1–4) – НКП, вращательная, 5 класса;
4. (2–3) – НКП, вращательная, 5 класса;
5. (3–0) – НКП, поступательная, 5 класса;
6. (4–5) – НКП, вращательная, 5 класса;
7. (5–0) – НКП, поступательная, 5 класса.
Таким образом, ![]()
Определение степени подвижности:
![]()
![]()
Выделение основного механизма – основной механизм это первое звено и стойка с соединяющей их кинематической парой.
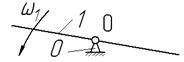
Рисунок 1.2.2. Основной механизм первого класса
Выделение 1-й в порядке наслоения группы Ассура – звено 2–3, 4–5.
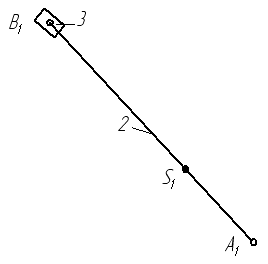
Рисунок 1.2.3. Первая в порядке наслоения группа Ассура 2-го класса 2-го вида
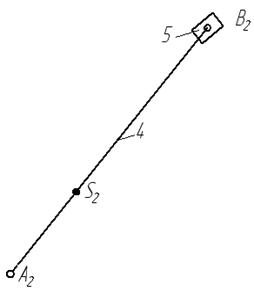
Рисунок 1.2.4. Вторая в порядке наслоения группа Ассура 2-го класса 2-го вида
Определение класса механизма в целом. Механизм 2-го класса, так как в его состав входит структурная группа второго класса.
1.3 Кинематический анализ механизма
Метод замкнутых контуров устанавливает связь между геометрическими и кинематическими параметрами механизма и основан на условии замкнутости контуров. В механизмах 2-го класса количество замкнутых контуров равно количеству структурных групп 2-го класса, образующих механизм. Если звенья механизма принять за векторы, то в процессе движения конфигурация векторного многоугольника изменяется, но условие замкнутости сохраняется, т.е. в любом положении механизма геометрическая сумма векторов равна нулю.

Рисунок 1.3.1. Замкнутый векторный многоугольник
Кинематическая схема механизма приведена на рис. 1.3.1. Направляющие ползунов наклонены относительно системы координат ![]() . Целесообразно выбрать новую систему координат
. Целесообразно выбрать новую систему координат ![]() , начало
, начало ![]() которой совмещено с осью вращения кривошипа 1, а ось
которой совмещено с осью вращения кривошипа 1, а ось ![]() абсцисс ориентирована параллельно направляющим ползуна 3. Для однозначного определения направляющих углов
абсцисс ориентирована параллельно направляющим ползуна 3. Для однозначного определения направляющих углов ![]() и
и ![]() со звеньями 1 и 2 связываются векторами
со звеньями 1 и 2 связываются векторами ![]() . Длину шатуна 2 и положение точки
. Длину шатуна 2 и положение точки ![]() на шатуне выражено через длину
на шатуне выражено через длину ![]() кривошипа:
кривошипа: ![]()
![]()
Направляющий угол ![]() вектора
вектора ![]() :
:
![]()
где: ![]() координаты начала
координаты начала ![]() и конца
и конца ![]() вектора
вектора ![]() которые выражены в виде соотношений:
которые выражены в виде соотношений:
![]()
![]()
![]()
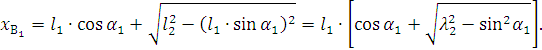
После подстановки уравнений ![]() в
в ![]() имеется:
имеется:

или
![]()
Функция положения точки ![]() ползуна 3 соответствует выражению
ползуна 3 соответствует выражению
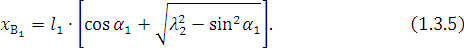
Функция положения точки ![]() на шатуне 2
на шатуне 2
![]()
![]()
Кинематические передаточные функции получаются путем дифференцирования соотношений ![]() по обобщенной координате
по обобщенной координате ![]() .
.
Передаточное отношение ![]() угловых скоростей шатуна и кривошипа
угловых скоростей шатуна и кривошипа
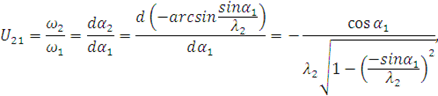
или окончательно
![]()
Передаточные функции скорости некоторых точек: точки ![]() на ползуне
на ползуне
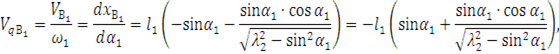
или окончательно
![]()
точки ![]() на шатуне:
на шатуне:
![]()
![]()
![]()
Угловое ускорение шатуна 2:
![]()
или
![]()
Передаточная функция углового ускорения шатуна 2 определяется соотношением
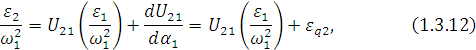
где:
![]()
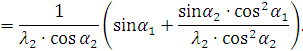
Окончательно получается
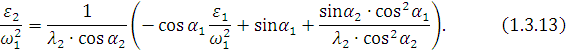
Отношение ускорения ![]() к квадрату угловой скорости
к квадрату угловой скорости ![]() точки
точки ![]() на ползуне равно
на ползуне равно
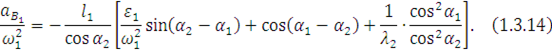
Действительные значения углового ускорения шатуна 2 и линейного ускорения точки ![]() ползуна 3 соответственно становят:
ползуна 3 соответственно становят:
![]()
![]()
Следуя методике, изложенной выше, получим
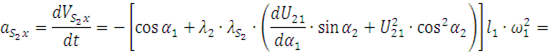
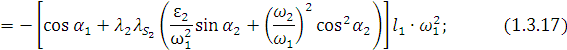
![]()
![]()
Результаты вычислений для 24 положений кривошипно-ползунного механизма приведены в таблицах ниже
Таблица 1.3.1. Результаты расчетов
|
|
|
|
|
|
|
|
|
|
| 0 | 0 | 14,3 | 0 | 2,9633 | -10 | -1,792 | -144 | 7,8606 |
| 30 | -7,18 | 11,0 | -1,754 | 2,5674 | -8,729 | -6,549 | -114,6 | -69,42 |
| 60 | -12,5 | 4,91 | -2,813 | 1,2173 | -5,121 | -9,431 | -43,21 | -130,6 |
| 90 | -14,5 | -2,49 | -2,88 | -0,623 | 0 | -9,857 | 29,745 | -140,6 |
| 120 | -12,5 | -9,25 | -2,175 | -2,21 | 5,1215 | -7,761 | 71,987 | -93,77 |
| 150 | -7,18 | -13,6 | -1,126 | -2,944 | 8,7287 | -3,519 | 84,907 | -16,91 |
| 180 | 0 | -14,3 | 0 | -2,709 | 10 | 1,7916 | 86,4 | 47,869 |
| 210 | 7,18 | -11,0 | 1,1258 | -1,845 | 8,7287 | 6,5491 | 84,907 | 78,683 |
| 240 | 12,5 | -4,91 | 2,1748 | -0,753 | 5,1215 | 9,4315 | 71,987 | 85,921 |
| 270 | 14,5 | 2,49 | 2,88 | 0,3769 | 0 | 9,8574 | 29,745 | 86,308 |
| 300 | 12,5 | 9,25 | 2,8135 | 1,492 | -5,121 | 7,7613 | -43,21 | 82,728 |
| 330 | 7,18 | 13,6 | 1,7542 | 2,4682 | -8,729 | 3,5187 | -114,6 | 61,896 |
| 360 | 0 | 14,3 | 0 | 2,9633 | -10 | -1,792 | -144 | 7,8606 |
| 390 | -7,18 | 11,0 | -1,754 | 2,5674 | -8,729 | -6,549 | -114,6 | -69,42 |
| 420 | -12,5 | 4,91 | -2,813 | 1,2173 | -5,121 | -9,431 | -43,21 | -130,6 |
| 450 | -14,5 | -2,49 | -2,88 | -0,623 | 0 | -9,857 | 29,745 | -140,6 |
| 480 | -12,5 | -9,25 | -2,175 | -2,21 | 5,1215 | -7,761 | 71,987 | -93,77 |
| 510 | -7,18 | -13,6 | -1,126 | -2,944 | 8,7287 | -3,519 | 84,907 | -16,91 |
| 540 | 0 | -14,3 | 0 | -2,709 | 10 | 1,7916 | 86,4 | 47,869 |
| 570 | 7,18 | -11,0 | 1,1258 | -1,845 | 8,7287 | 6,5491 | 84,907 | 78,683 |
| 600 | 12,5 | -4,91 | 2,1748 | -0,753 | 5,1215 | 9,4315 | 71,987 | 85,921 |
| 630 | 14,5 | 2,49 | 2,88 | 0,3769 | 0 | 9,8574 | 29,745 | 86,308 |
| 660 | 12,5 | 9,25 | 2,8135 | 1,492 | -5,121 | 7,7613 | -43,21 | 82,728 |
| 690 | 7,18 | 13,6 | 1,7542 | 2,4682 | -8,729 | 3,5187 | -114,6 | 61,896 |
| 720 | 0 | 14,3 | 0 | 2,9633 | -10 | -1,792 | -144 | 7,8606 |
Таблица 1.3.2. Результаты расчетов
|
|
|
|
|
|
|
|
| 0 | 1,92 | 2,8978 | 124,8 | 76,387 | 0 | -405,6 |
| 30 | 2,2696 | 2,6337 | 111,48 | 93,313 | 191,98 | -303,8 |
| 60 | 2,7721 | 2,0938 | 84,887 | 118,61 | 349,01 | -129,7 |
| 90 | 2,88 | 1,9668 | 77,437 | 123,21 | 413,12 | 65,303 |
| 120 | 2,5735 | 2,4593 | 91,237 | 102,66 | 349,01 | 250,69 |
| 150 | 2,1325 | 2,862 | 102,35 | 78,892 | 191,98 | 383,71 |
| 180 | 1,92 | 2,8137 | 105,6 | 81,111 | 0 | 405,62 |
| 210 | 2,1325 | 2,4236 | 102,35 | 95,849 | -192 | 303,83 |
| 240 | 2,5735 | 2,0196 | 91,237 | 104,2 | -349 | 129,68 |
| 270 | 2,88 | 1,9458 | 77,437 | 105,26 | -413,1 | -65,3 |
| 300 | 2,7721 | 2,2719 | 84,887 | 99,58 | -349 | -250,7 |
| 330 | 2,2696 | 2,7078 | 111,48 | 86,086 | -192 | -383,7 |
| 360 | 1,92 | 2,8978 | 124,8 | 76,387 | 0 | -405,6 |
| 390 | 2,2696 | 2,6337 | 111,48 | 93,313 | 191,98 | -303,8 |
| 420 | 2,7721 | 2,0938 | 84,887 | 118,61 | 349,01 | -129,7 |
| 450 | 2,88 | 1,9668 | 77,437 | 123,21 | 413,12 | 65,303 |
| 480 | 2,5735 | 2,4593 | 91,237 | 102,66 | 349,01 | 250,69 |
| 510 | 2,1325 | 2,862 | 102,35 | 78,892 | 191,98 | 383,71 |
| 540 | 1,92 | 2,8137 | 105,6 | 81,111 | 0 | 405,62 |
| 570 | 2,1325 | 2,4236 | 102,35 | 95,849 | -192 | 303,83 |
| 600 | 2,5735 | 2,0196 | 91,237 | 104,2 | -349 | 129,68 |
| 630 | 2,88 | 1,9458 | 77,437 | 105,26 | -413,1 | -65,3 |
| 660 | 2,7721 | 2,2719 | 84,887 | 99,58 | -349 | -250,7 |
| 690 | 2,2696 | 2,7078 | 111,48 | 86,086 | -192 | -383,7 |
| 720 | 1,92 | 2,8978 | 124,8 | 76,387 | 0 | -405,6 |
1.4 Силовой расчет механизма при ![]() ,
, ![]() ,
, ![]() и
и ![]()
Цель этого этапа исследования – определение реакций в кинематических парах механизма и величины действующего момента, приложенного к кривошипу механизма.
Определение движущей силы при помощи давления ![]() рабочего тела в цилиндре и диаметра поршня
рабочего тела в цилиндре и диаметра поршня ![]() :
:
![]()
Таблица 1.4.1. Движущие силы и давления в цилиндрах
|
|
|
|
|
|
| 0 | 1,38 | 15607,43 | 0,03 | 339,292 |
| 30 | 2,64 | 29857,7 | 0,03 | 339,292 |
| 60 | 1,14 | 12893,1 | 0,02 | 227,33 |
| 90 | 0,54 | 6107,256 | 0 | 0 |
| 120 | 0,3 | 3392,92 | -0,01 | -112 |
| 150 | 0,21 | 2375,044 | -0,03 | -339,292 |
| 180 | 0,15 | 1696,46 | -0,03 | -339,292 |
| 210 | 0,03 | 339,292 | -0,03 | -339,292 |
| 240 | 0,03 | 339,292 | -0,02 | -227,33 |
| 270 | 0,03 | 339,292 | -0,01 | -112 |
| 300 | 0,03 | 339,292 | 0,03 | 339,292 |
| 330 | 0,03 | 339,292 | 0,04 | 451,26 |
| 360 | 0 | 0 | 0,13 | 1469,134 |
| 390 | 0 | 0 | 0,45 | 5089,38 |
| 420 | -0,03 | -339,292 | 1 | 11308,6 |
| 450 | -0,03 | -339,292 | 1,8 | 20357,52 |
| 480 | -0,03 | -339,292 | 2,14 | 24201,7 |
| 510 | -0,03 | -339,292 | 0,94 | 10630,02 |
| 540 | 0 | 0 | 0,46 | 5201,346 |
| 570 | 0,03 | 339,292 | 0,27 | 3053,628 |
| 600 | 0,03 | 339,292 | 0,19 | 2147,718 |
| 630 | 0,06 | 678,584 | 0,11 | 1245,202 |
| 660 | 0,27 | 3053,628 | 0,03 | 339,292 |
| 690 | 0,81 | 9160,884 | 0,03 | 339,292 |
| 720 | 1,38 | 15607,43 | 0,03 | 339,292 |
Используя построенный план ускорений, определим силы и моменты сил инерции, действующие на звенья механизма в процессе движения:
![]()
![]()
положение 2:
![]()
![]()
![]()
![]()
![]()
![]()
положение 5:
![]()
![]()
![]()
![]()
![]()
![]()
положение 21:
![]()
![]()
![]()
![]()
![]()
![]()
положение 24:
![]()
![]()
![]()
![]()
![]()
![]()
Определив направления сил и моментов сил инерции с помощью плана ускорений (силы инерции противоположно направлены ускорениям центров масс звеньев механизма, а моменты сил инерции противоположно направлены угловым ускорениям звеньев механизма), и перенеся их на схему механизма. Разобьем его на части согласно проведенному структурному анализу. Рассмотрим группу Ассура звенья 2–3. Запишем сумму моментов относительно точки ![]() :
:
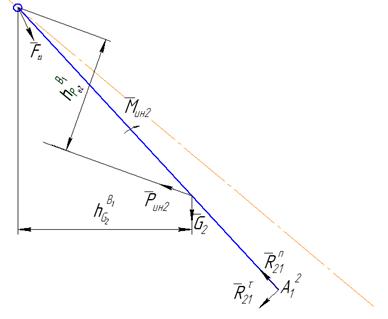
Рисунок 1.4.1. Плечи сил
положение 2:
![]()
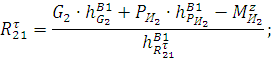
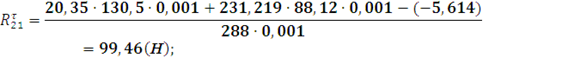
положение 5:
![]()
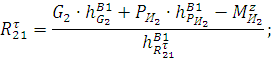
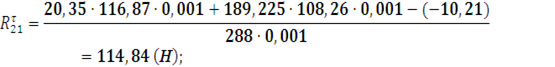
положение 21:
![]()
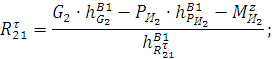
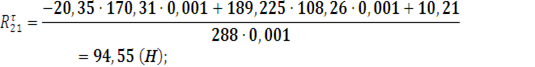
положение 24:
![]()
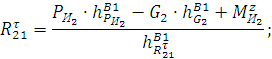
![]()
где: ![]() и
и ![]() – плечи силы тяжести
– плечи силы тяжести ![]() и силы инерции
и силы инерции ![]() , соответственно.
, соответственно. ![]() – проекция момента на ось z, направление которой к нам перпендикулярно плоскости чертежа.
– проекция момента на ось z, направление которой к нам перпендикулярно плоскости чертежа.
Запишем уравнение суммы сил:
![]()
В уравнении (1.4.4) неизвестны по модулю силы ![]() и
и ![]() , так как в уравнении два неизвестных, то можно построить план сил, откуда и определим неизвестные силы.
, так как в уравнении два неизвестных, то можно построить план сил, откуда и определим неизвестные силы.
Для каждого положения выбрано масштаб плана сил ![]() :
:
Тогда отрезки соответствующие известным силам будут равны:
положение 2:
![]()
![]()
![]()
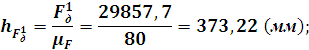
![]()
![]()
положение 5:
![]()
![]()
![]()
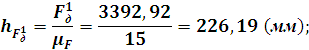
![]()
![]()
положение 21:
![]()
![]()
![]()
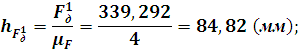
![]()
![]()
положение 24:
![]()
![]()
![]()
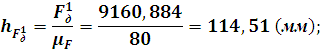
![]()
![]()
Построив план сил, определяем:
положение 2:
![]()
![]()
![]()
положение 5:
![]()
![]()
![]()
положение 21:
![]()
![]()
![]()
положение 24:
![]()
![]()
![]()
Рассмотрим звено 3, записав уравнение суммы сил, определим реакцию ![]() используя ранее построенный план сил:
используя ранее построенный план сил:
![]()
Из плана сил определяем:
положение 2:
![]()
положение 5:
![]()
положение 21:
![]()
положение 24:
![]()
Рассмотрим группу Ассура звенья 4–5. Запишем сумму моментов относительно точки ![]() :
:
положение 2:
![]()
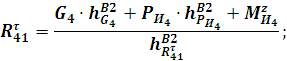

положение 5:
![]()
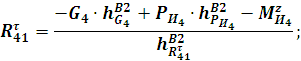
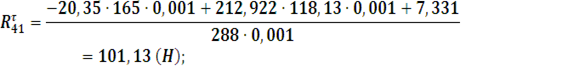
положение 21:
![]()
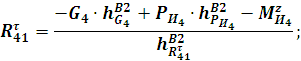
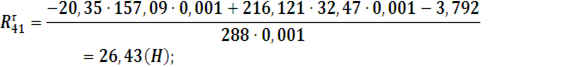
положение 24:
![]()
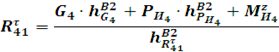
где: ![]() и
и ![]() – плечи силы тяжести
– плечи силы тяжести ![]() и силы инерции
и силы инерции ![]() , соответственно.
, соответственно.
![]() – проекция момента на ось z, направление которой к нам перпендикулярно плоскости чертежа.
– проекция момента на ось z, направление которой к нам перпендикулярно плоскости чертежа.
Запишем уравнение суммы сил:
![]()
В уравнении (1.37) неизвестны по модулю силы ![]() и
и ![]() , так как в уравнении два неизвестных, то можно построить план сил, откуда и определим силы
, так как в уравнении два неизвестных, то можно построить план сил, откуда и определим силы ![]() и
и ![]() .
.
Для каждого положения выбрано масштаб плана сил ![]() :
:
Тогда отрезки соответствующие известным силам будут равны:
положение 2:
![]()
![]()
![]()
![]()
![]()
![]()
положение 5:
![]()
![]()
![]()
![]()
![]()
![]()
положение 21:
![]()
![]()
![]()
![]()
![]()
![]()
положение 24:
![]()
![]()
![]()
![]()
![]()
![]()
Построив план сил, определяем:
положение 2:
![]()
![]()
![]()
положение 5:
![]()
![]()
![]()
положение 21:
![]()
![]()
![]()
положение 24:
![]()
![]()
![]()
Рассмотрим звено 5, записав уравнение суммы сил, определим реакцию ![]() , используя ранее построенный план сил:
, используя ранее построенный план сил:
![]()
Из плана сил определяем:
положение 2:
![]()
положение 5:
![]()
положение 21:
![]()
положение 24:
![]()
Рассмотрим основной механизм первое звено.
Составим сумму моментов относительно точки О, учитывая,
что ![]() и
и ![]() :
:
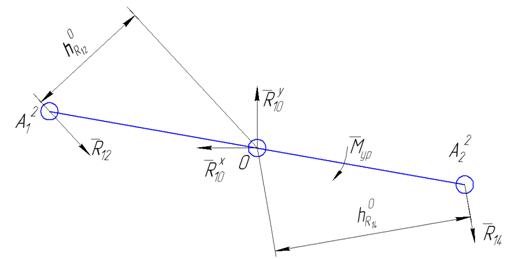
Рисунок 1.4.2. Плечи сил
![]()
При этом плечи будут равны:
![]()
![]()
![]()
положение 5:
![]()
При этом плечи будут равны:
![]()
![]()
![]()
положение 21:
![]()
При этом плечи будут равны:
![]()
![]()
![]()
положение 24:
![]()
При этом плечи будут равны:
![]()
![]()
![]()
Для нахождения реакции ![]() составим уравнение суммы сил действующих на основной механизм:
составим уравнение суммы сил действующих на основной механизм:
![]()
Для построения каждого плана сил выберано масштабный коэффициент![]() :
:
Тогда отрезки соответствующие силам ![]() и
и ![]() будут равны:
будут равны:
положение 2:
![]()
![]()
положение 5:
![]()
![]()
положение 21:
![]()
![]()
положение 24:
![]()
![]()
Из плана находим:
положение 2:
![]()
положение 5:
![]()
положение 21:
![]()
положение 24:
![]()
Похожие работы
... 24 0,00 0,00 14,10 14,10 9,30 9,30 58,02 58,02 2.4 Исследование механизма методом кинематических диаграмм Исследование механизмов методом диаграмм производится с целями: 1. Получения наглядного представления о законе движения интересующей нас точки или звена механизма. 2. Определения скоростей и ускорений точек или звеньев на основе известного закона перемещений точек или ...
... двигателя и улучшения его показателей в соответствии с уровнем развития техники. ЛИТЕРТУРА 1. Б.Е.Железко, В.М.Адамов, И.К.Русецкий, Г.Я.Якубенко / Расчет и конструирование автомобильных и тракторных двигателей (Дипломное проектирование): Учебное пособие для вузов / Мн.:"Высшая школа", 1987 г. 2. А.И.Колчин, В.П.Демидов / Расчет автомобильных и тракторных двигателей. Учебник для ВУЗов / ...
... электроэнергии, воды, местные вентиляционные отсосы, нахождения аптечки и средств пожаротушения. 6. Конструкторская разработка 6.1 Анализ существующих конструкций и приспособлений для обкатки и испытания двигателей внутреннего сгорания Приработка и испытания двигателей внутреннего сгорания производятся на обкаточно-тормозных стендах переменного тока, включающих устройство для вращения ...
... и точки расширения соединяем плавными кривыми. После этого достраиваем процессы газообмена. Полученная индикаторная диаграмма двигателя внутреннего сгорания дизеля MAN изображена на рисунке 14.1. Рисунок 14.1 - Индикаторная диаграмма ДВС MAN. Выводы Результаты расчетов и общепринятые границы изменения расчетных параметров сводим в таблицу. Таблица - Результаты расчетов. НАЗВАНИЕ ...
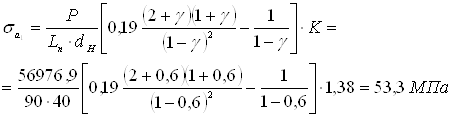
0 комментариев