Навигация
3 Проверочный расчёт
Расчет долговечности подшипников качения
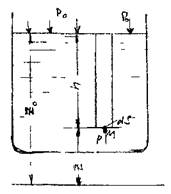
Приводной вал может быть представлен следующей расчетной схемой.
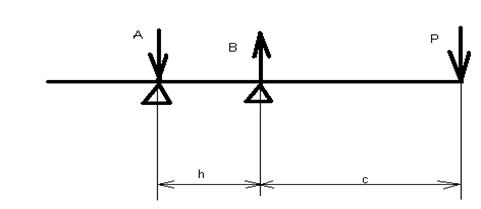
На схеме приняты следующие обозначения: h = 40 мм - расстояние между подшипниками А (№ 46306) и В (№ 46306);
с = 100 мм - расстояние от подшипника В до силы Р
Согласно [2, с.172]:
![]()
где ![]() площадь поршня.
площадь поршня.
Определяем реакции А, В :
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
Определение долговечности подшипников
В соответствии с [3, с.393] расчетный срок службы подшипника качения в часах определяется по формуле:
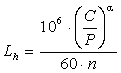 ,
,
где С - каталожная динамическая грузоподъемность данного типоразмера подшипника, Н;
α - степенной показатель: α = 3 - для шарикоподшипников, α = 3,3 - для роликоподшипников;
![]() - эквивалентная нагрузка подшипника в Н, для определения которой принимаем:Y= 0 и X = 1, в соответствии с [3, с.395 - 397];
- эквивалентная нагрузка подшипника в Н, для определения которой принимаем:Y= 0 и X = 1, в соответствии с [3, с.395 - 397];
V= 1, т.к. относительно вектора нагрузки вращается внутреннее кольцо;
Fa = 0, т.к. осевая нагрузка отсутствует;
kб = 1 - коэффициент безопасности для спокойной без толчков нагрузки; kТ = 1, для температуры до 100°С;
Fr- радиальная нагрузка, определенная выше (А, В,).
Таким образом, и для шарикоподшипника и для роликоподшипников гидромашины:
Р = Fr .
После подстановки значений n ,α и Fr получим выражение для определения срока службы:
шарикоподшипника 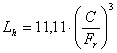 ;
;
роликоподшипников 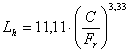
Подставляя в формулу для шарикоподшипника №46306 табличное значение С и рассчитанное выше значение Рr, определим его срок службы:
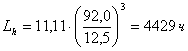 .
.
Аналогично для роликоподшипника № 42306 :
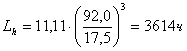 .
.
Определение усилия пружин, обеспечивающего прижим подпятников к опорному диску
Расчеты производятся по методике изложенной в [2, с.165-172 ].
Усилие пружин определяется по выражению:
Pпр=∑Pimax +∑P1 +∑P2+∑P3+∑P4 ,
где ∑Pimax - максимальная суммарная сила инерции, действующая на плунжера, соединенные с подпятниками;
∑P1 - усилие пружины подпятников, предотвращающее поворот их под действием центробежной силы инерции;
∑P2 - усилие, необходимое для перемещения плунжеров при ходе всасывания, создающееся вследствие разряжения под плунжерами;
∑P3 - усилие, создающее уплотнение между торцом подпятника и плоскостью опорного диска;
∑P4 - усилие, обусловленное трением плунжеров.
Определение силы Pimax
Расчет производится по [2, ф. 2.162]:
∑Pi max =ξ·ω2·mn·r·tgb
где ξ= 3,17 - коэффициент для z= 7 шт. плунжеров; ξ= 2,88 - коэффициент для z= 9 шт. плунжеров; ξ= 2,53 - коэффициент для z= 11 шт. плунжеров;
![]() -частота вращения ротора;
-частота вращения ротора;
mn » 0,1…0,4 кг. масса плунжера с подпятником, принято mn=0,32 кг;
r = 0,048 м - радиус расположения плунжеров в роторе.
Подставляя значения входящих величин в формулу, получим:
∑Pimax=2,88·1572·0,32·0,0225·tg18º=166 Н.
Определение усилия Р1
Расчет производится по [2, ф. 2.165]:
![]() ,
,
где m0 » 0,02…0,07 кг - масса подпятника, принято m0 = 0,054 кг;
e = 10,82 мм расстояние от центра тяжести подпятника до центра сферической головки плунжера.
Подставляя значения в формулу, получим выражения силы ∑P1:
![]() Н.
Н.
Определение усилия ∑P2
Расчет производится по [2, ф. 2.166]:
![]() ,
,
где Pв = 0,05 МПа - допустимое разрежение в поршневой камере;
F = 2,0 × 10-4 м2 - площадь сечения плунжера.
Подставляя значения в формулу, получим:
![]() Н.
Н.
Определение усилия ∑P3
Расчет производится по [2, ф. 2.168]:
![]() ,
,
где F1 - площадь кольцевых поверхностей подпятника за вычетом площади дренажных пазов;
σв = 0,1 МПа - удельное давление на поверхностях скольжения, необходимое для создания достаточного уплотнения, препятствующего засасыванию воздуха через стык между ними.
![]()
После вычислений:
![]() Н.
Н.
Определение усилия ∑P4
Расчет производится по [2, ф. 2.170]:
![]() ,
,
где μ=0,05 – коэффициент трения;
![]() .
.
![]()
Таким образом, минимальное усилие пружин по [2, ф. 2.159] равно:
Pпр=∑Pimax +∑P1 +∑P2+∑P3+∑P4 .
Подставив ранее полученные значения, получим:
![]()
К этой величине следует прибавить согласно [2, ф. 2.171] запас:
![]() .
.
Подставив ранее полученные значения, получим:
![]()
Тогда полное требуемое усилие пружин составит :
![]()
Расчет вала ротора
Определение запаса прочности
Вал ротора нагружен крутящим моментом и поперечными силами вызывающими изгиб.
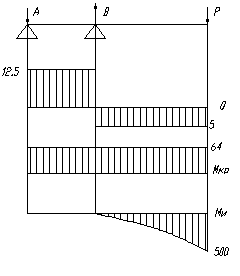
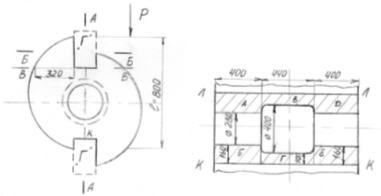
Рис.9. Расчет вала ротора
Крутящий момент, передаваемый валом:
![]()
где N – мощность, потребляемая насосом.
Изгибающий момент в опасном сечении:
![]()
Расчетное сечение вала представляет собой шлицевое сечение с наружным диаметром Дн=2,2 см и внутренним Дв=1,8 см, для которого определяем моменты сопротивления.
Осевой: 
Полярный: ![]()
Определяем напряжения в расчетном сечении от изгиба:
![]()
Определяем напряжения в расчетном сечении от кручения:
![]()
Механические свойства стали 40X (закалка с нагревом ТВЧ) из которой изготавливается вал, имеет следующие справочные данные:
предел прочности σв = 850 МПа;
предел текучести σт = 700 МПа;
предел выносливости при изгибе σ-1 = 560 МПа.
Тогда согласно [5, с.107] определяем коэффициент запаса прочности по нормальным напряжениям:
![]() .
.
По касательным напряжениям расчет производится по [4, с.219]:
![]() ,
,
где τТ - предел текучести вала по касательным напряжениям. Согласно энергетической теории прочности, наиболее верной для пластичных материалов:
![]() .
.
Запас прочности по статической несущей способности для пластичного материала определяется [5, с.219]:
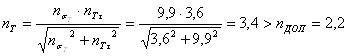 ,
,
где nДОП = 2,2 - допускаемая величина запаса прочности.
Определение прогиба вала ротора
Определение прогиба вала ротора в сечение k (см. рис.8):
![]() .
.
Это выражение справедливо в предположении постоянной по длине жесткости вала. Условно будем считать, что вал имеет жесткость, равную жесткости прослабленного шлицевого участка с наружным диаметром ДН, внутренним ДВ, шириной зуба b и числом зубьев Z:
Из предварительного расчета шлицевое соединение имеет следующие параметры:
Момент сечения определим по формуле:
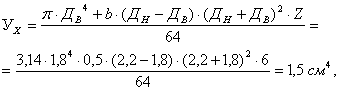
![]() .
.
Тогда прогиб вала:
![]() .
.
Проверка шлиц вала на смятие
Допускаемые напряжения смятия на боковых поверхностях шлицевых зубьев для данных условий эксплуатации, согласно [3, с.383] :
![]() .
.
Фактическое напряжение смятия, согласно [3, с.382]:
![]() ,
,
где Мк - крутящий момент, передаваемый валом;
ψ = 0,75 коэффициент, учитывающий неравномерное распределение нагрузки между зубьями;
z - число зубъев;
l - длина зубъев;
h - высота поверхности контакта зубъев, измеренная по радиусу;
rср - расстояние от оси вала до поверхности контакта.
Высота поверхности контакта зубъев определяется по [3, с.383]:
![]() ,
,
где f-= 0,04 – коэффициент трения на поверхности шлицов.
Расстояние от оси вала до поверхности контакта находится по выражению:
![]() .
.
Тогда фактическое напряжение смятия:
![]() .
.
Прочность зубьев на смятие обеспечена, т.к. полученное значение находится в пределах допустимого.
Проверка плотности загруженности стыков
Расчеты производятся по [2, с.165-166].
Для того, чтобы максимально уменьшить утечки по подвижным стыкам насоса (трущиеся пары "подпятник - опорный диск" и "распределительный диск - ротор"), необходимо обеспечить уплотняющее усилие при минимальном давлении рабочей жидкости с тем условием, чтобы при максимальном удельные давления в стыке не превышали допускаемых.
Расчет стыка "подпятник - опорный диск"
Начальное уплотнение по торцу подпятника в рассматриваемой конструкции создается пружинами ротора. При этом должно быть обеспечено удельное давление в стыке при ходе всасывания σв = 0,1 МПа.
С другой стороны, при ходе нагнетания удельное давление на торце подпятника не должны превышать допускаемого значения [2, с.166].:
[σn]=2,5 – 3,0 МПа.
Силы, действующие на стык "подпятник - опорный диск", показаны на рис. 4.
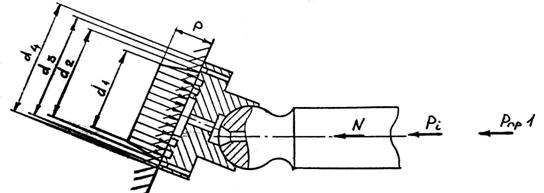
Рис.10. Схема сил действующих на стык "подпятник - опорный диск"
Определение удельных давлений на торце подпятника.
а) усилие гидравлического прижима рассчитывается по [2, ф. 2.136]:
![]() ;
;
б) усилие пружины, приходящееся на один плунжер рассчитывается по [2, ф. 2.136]:
![]() ;
;
в)усилие отжима Р0, возникающего на поверхности выточки d1 подпятника и в зазоре опорного поиска.
Усилие Р0 определяется из условия, что в выточке подпятника действует рабочее давление Р, что обычно и соблюдается, так как утечка жидкости пренебрежимо мала. Можно принять, что в торцовом зазоре между кольцевой поверхностью подпятника, ограниченной диаметрами d1 и d2, разность между которыми мала и поверхностью опорного диска, давление распределяется по линейному закону.
Тогда усилие конуса высотой Р и диаметрами d1 и d2 :
![]() .
.
г) удельное давление σn на торцовой поверхности подпятника при ходе нагнетания плунжеров (без учета силы трения между поршнем и ротором) рассчитывается по [2, ф. 2.139]:
![]() ,
,
где F1 =3,2 см2 - площадь кольцевых поверхностей опоры;
Рi - сила инерции подпятника с плунжером:
![]() .
.
После подстановки получим:
![]() .
.
Условие выполняется.
Расчет стыка ''распределительный диск - ротор"
Расчет производятся по [2, с.184-190].
Для того, чтобы обеспечить надежный прижим ротора к распределительному диску, должен быть произведен соответствующий расчет, исключающий возможность раскрытия стыка.
На рис.5 представлена эпюра распределения давления по торцу ротора (заштрихованная трапецеидальная площадка). При этом кольцевая площадка, лежащая на торце ротора против окна "а", в распределительном диске нагружается полным давлением рабочей жидкости, а площадки с размерами![]() и
и![]() нагружаются давлением, распределенным по треугольнику.
нагружаются давлением, распределенным по треугольнику.
В результате на торец ротора действуют силы P1, P2, Р3 величины которых определяются следующими уравнениями:
![]() .
.
![]() .
.
![]() .
.
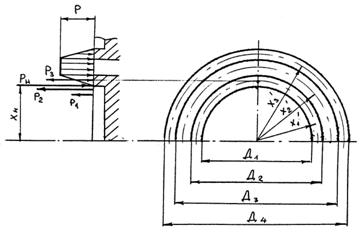 Рис.11. Эпюра распределения давления по торцу ротора
Рис.11. Эпюра распределения давления по торцу ротора Сила РH, прижимающая ротор к торцу распределительного диска, определяется уравнением:
![]() .
.
Для того чтобы предотвратить раскрытие стыка между ротором и распределительным диском, должно быть обеспечено превышение ΔР сил, прижимающих ротор, над силами, отжимающими ротор от распределительного диска. Это условие записывается так [2, ф. 2.224]:
![]() .
.
На основании опытных данных в общем случае должно быть соблюдено [2, ф. 2.226]:
![]() , тогда
, тогда![]() .
.
Кроме соблюдения условия, выражаемого [2, ф. 2.226], должно быть также обеспечено превышение момента ΔМ, создаваемого силой РH относительно оси ротора, над суммой моментов, создаваемых силами P1, P2, P3 относительно той же оси. Это условие записывается следующим образом:
![]() ,
,
где ХH, X1, X2, X3 - точки приложения сил.
Указанные силы рассматриваются как равнодействующие равномерно распределительной нагрузки, действующей по полукольцам со средними радиусами соответственно X1′, X2′, X3′ которые определяются по следующим уравнениям:
![]() [2, ф. 2.215];
[2, ф. 2.215];
![]() [2, ф. 2.216];
[2, ф. 2.216];
![]() [2, ф. 2.217];
[2, ф. 2.217];
Точки приложения указанных сил определяются как центры тяжести полуколец со средними радиусами X1′, X2′, X3′ :
![]() [2, ф. 2.218];
[2, ф. 2.218];
![]() [2, ф. 2.219];
[2, ф. 2.219];
![]() [2, ф. 2.220];
[2, ф. 2.220];
![]() .
.
Таким образом:
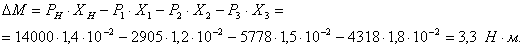
![]()
Полученное значение находится в пределах допустимых значений согласно условию [2, ф. 2.226] :
![]() .
.
Удельное давление на плоскости контакта ротора и распределительного диска определяется по [2, ф. 2.227]:
![]() ,
,
где ∑f - суммарная площадь уплотняющих поясков и разгрузочных площадок.
[σ] = 1,4 МПа - допустимое удельное давление [2, с189].
![]()
![]() .
.
Определение удельных давлений в сопряжениях деталей
Удельные давления на поверхностях контакта деталей не должны превышать допускаемых значений для каждого конкретного материала.
Расчет удельных давлений в сопряжении "шаровая втулка –
прижимной диск"
Расчет проведем для нейтрального положения диска.
При расчете будем исходить из условия, что удельные давления на поверхности контакта изменяются по синусоидальному закону (рис. 12).
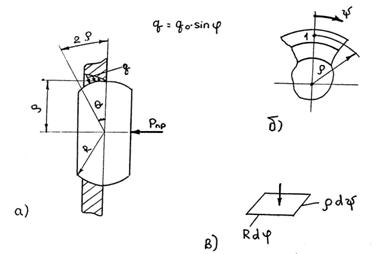
Рис.12. Схема к расчету удельных давлений в сопряжении "шаровая втулка – прижимной диск":
где q0 - максимальное значение удельных давлений; φ - угол, отсчитываемый вдоль образующей шарового пояса от вертикальной плоскости, проходящей через центр сферы.
Определим удельные давления на поверхности контакта шаровой втулки и прижимного диска.
Равнодействующая Q горизонтальных составляющих сил давления на поверхности контакта уравновешивает усилие центральной пружины:
РПР = Q.
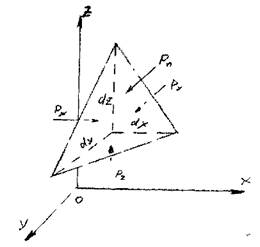
Для определения горизонтальной равнодействующей сил давления Q вырежем в точке 1 (см. рис.12) элементарную площадку шарового пояса, отстоящую от оси пояса на расстоянии ρ (pиc.12, в), со сторонами Rdφ и ρdψ. Элементарная площадь равна:
![]()
где R - радиус сферической поверхности;
ψ - угол, отсчитываемый в направлении, перпендикулярном образующей шарового пояса (рис.6, б).
Радиус положения элементарной площадки:
![]() ,
,
тогда ![]() ,
,
Давление, действующее на площадку dS:
![]() .
.
Горизонтальная проекция этой элементарной силы:
![]() .
.
Горизонтальная равнодействующая сил давления:
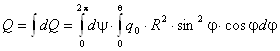 ,
,
где θ – угол контакта (см. рис.6).
Решив данный интеграл, находим:
![]() .
.
Приравнивая это положение усилию пружины РПР, определяем:
![]() ,
,
где h - толщина нажимного диска в пределах зоны контакта;
![]() - синус угла контакта.
- синус угла контакта.
Тогда:
![]() .
.
После вычислений получим:
![]() .
.
Определим удельное давление q при φ = θ
![]() .
.
С изменением угла наклона прижимного диска удельные давление на поверхности его контакта с шаровой втулкой изменяются обратно пропорционально косинусу этого угла:
![]() .
.
После вычислений получим:
![]() .
.
Расчет удельных давлений в сопряжении ''плунжер-ротор''
В расчете будем исходить из условия, что плунжер консольно нагружен вертикальной составляющей РВ реакции N нажимного диска (рис.13 а), её горизонтальная составляющая Рr уравновешена силой давления рабочей жидкости:
![]() ;
;
![]() .
.
Примем также, что удельное давление на поверхности контакта в каждом поперечном сечении плунжера изменяются по синусоидальному закону (рис. 13, б):
![]() ,
,
где ψ - угол, отсчитываемый от диаметральной плоскости плунжера, перпендикулярной вектору силы РB, вдоль направляющей поверхности контакта.
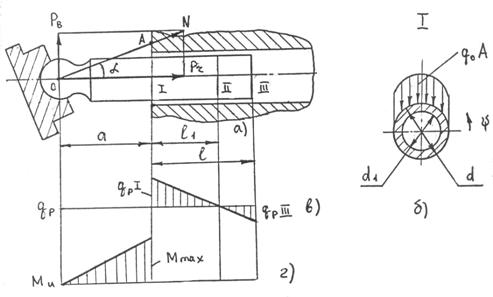
Рис.13 Схема к расчету удельных давлений в сопряжении ''плунжер-ротор''
Будем считать, что вдоль образующей поверхности контакта равнодействующая qP удельных давлений в поперечной сечении изменяется линейно.
Для определения положения нейтрального сечения II запишем уравнение моментов относительно точки 0:
![]() ,
,
где qp1, qp3 - равнодействующие удельных давлений в поперечных сечениях 1 и 3 соответственно;
a - вылет плунжера;
l - длина части плунжера в роторе;
l1 - расстояние от торца ротора до нейтрального сечения плунжера 2.
Учитывая соотношение (см. рис.13, в):
![]()
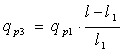 ,
,
решая уравнение моментов относительно l1, получим,:
![]() .
.
Легко убедиться, что ![]() , а значит
, а значит ![]() .
.
Равнодействующая удельных давлений в любом сечении:
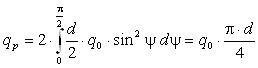 .
.
Для определения равнодействующей в опасном сечении I составим уравнение проекций сил на направление силы Рв с учетом qp3 .
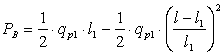 .
.
Подставляя выражения Pв и l1, получим:
![]() ,
,
откуда ![]()
Наибольший вылет плунжера amax = 38,3 мм.
Длина плунжера в роторе l = 71,7 мм.
Тогда, подставляя значения величин, получим:![]() .
.
Определение скорости потока
Расчет производится по [2, с.184-185].
Скорость потока рабочей жидкости в узких сечениях не должны превышать допустимых значений, установленных экспериментальным путем.
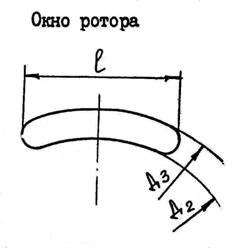
Рис.14. Схема к определению скорости потока
Расчет скорости потока жидкости в окнах ротора
Скорость рабочей жидкости в распределительных окнах ротора определяется согласно [2, ф.2.208]:
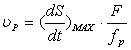 ,
,
где ![]() - наибольшая скорость плунжера в роторе, определяемая по [2, ф.2.142]:
- наибольшая скорость плунжера в роторе, определяемая по [2, ф.2.142]: ![]() ;
;
fp – площадь окна ротора, определяемая по [2, ф.2.208] :
![]()
Тогда, подставив числовые значения:
![]() .
.
Согласно опытным данным должно соблюдаться:
![]() - условие выполняется;
- условие выполняется;
![]() - условие выполняется.
- условие выполняется.
Расчет скорости потока жидкости в окне распределительного диска
Скорость потока жидкости в окне распределительного диска определяется по формуле:
![]() ,
,
где f0 – площадь окна распределительного диска:
![]() ,
,
где Xa = 159° – угол, на котором расположено окно распределительного диска.
Тогда, подставив числовые данные:
![]() .
.
![]() .
.
Согласно опытным данным должно соблюдаться:
![]() - условие выполняется
- условие выполняется
Заключение
В курсовом проекте была спроектирована аксиально-поршневая гидромашина со следующими техническими характеристиками: объёмная постоянная V0=20 ![]() , максимальное рабочее давление Рмах=20 МПа, номинальная частота вращения вала n=1500 об/мин., объёмный КПД
, максимальное рабочее давление Рмах=20 МПа, номинальная частота вращения вала n=1500 об/мин., объёмный КПД ![]() , гидромеханический КПД
, гидромеханический КПД ![]() , аналог разрабатываемой гидромашины - Г13….
, аналог разрабатываемой гидромашины - Г13….
В курсовом проекте был произведен предварительный и уточнённый расчёт гидромашины, рассчитана мощность гидромашины N=10кВт и определён крутящий момент на её валу, который составил 64 Н·м. Также в курсовом проекте была проверена шпонка на срез и смятие на выходном конце вала и произведена проверка плотности и загруженности стыков, определена скорость потока жидкости в окне распределительного диска и в окнах ротора, которые составили, соответственно, 2,2 м/с и 2 м/c.
Литература
1. Андрианов Д.Н. Проектирование аксиально-поршневой гидромашины: Практическое руководство по выполнению курсового проекта по курсу ''Объемные гидравлические и пневматические машины'' для студентов специальности Т.05.11.00. –Гомель: Учреждение образования ''Гомельский государственный технический университет имени П.О. Сухого'', 2002. – 21 с.
2. Башта Т.М., Зайченко И.З., Ермаков В.В., Хаймович Е.М. Объемные гидравлические приводы, -М.: Машиностроение, 1969. - 512 с.
3. Справочник металлиста. Том I. Под редакцией С.А. Чернавокого и В.Ф. Рещикова -М.: Металлургия, 1976г. - 357 с.
4. Справочник расчетно-теоретический. Книга 1. Под редакцией А.А. Уманского, -М.: Машиностроение, 1962. - 476 с.
5. Биргер И.А., Шорр Б.Ф., Шнейдерович P.M. Расчет на прочность деталей машин. Справочное пособие. Под редакцией И.А. Биргера, -М.: Высшая школа, 1966. –342 с.
6. Цветные металлы и сплавы. Том 1. Под редакцией И.В. Кудрявцева, -М., Металлургия, 1967. –494 с.
7. Куклин М.Г., Куклина Г.С. Детали машин. – М.: Высшая школа, 1973.-382с.
8. Анурьев В.И. Справочник конструктора – машиностроителя: В 3-х
т. - 5-еизд., перераб. и доп., - М.: Машиностроение,1980. –Т.1 – 728с.
Похожие работы
... . Для оценки режима течения жидкости вводят специальный критерий; число кавитации К f ' 7. Истечение жидкости из отверстий и насадков > 7.1. Отверстие в тонкой стенке Одной из типичных задач гидравлики, которую можно назвать задачей прикладного характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. ...
... Мощность электродвигателя , кВт, привода дробилки рассчитывается по формуле , (11) где - удельный энергетический показатель дробилки, при дробимом материале известняке [1]; - производительность дробилки, м3/ч; - степень дробления, для роторной дробилки типоразмера 1250´1000 мм [1]; - средневзвешенный диаметр исходного продукта, м; ...
... машины широко используют в качестве гидродвигателей. Гидродвигатели используются в гидроприводах палубных механизмов. 6. Элементы объёмного гидропривода: рабочие жидкости; гидроаппаратура, гидролинии и гидроёмкости, кондиционеры рабочей жидкости Объемным гидроприводом наз совокупность объем гидромашин, гидроаппаратуры и вспомогательных устройств соед. с помощью гидролиний. Предназначена для ...
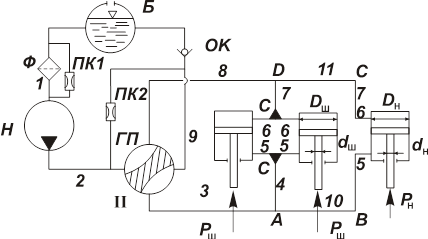
... Линия "Н" – участок трубопроводов в контуре ABCD, обслуживающих носовую стойку; Линия "Ш" – участок трубопроводов в контуре ABCD, обслуживающих основные стойки. Введение Гидравлические системы получили широкое применение в машиностроении, на транспорте, в технологических процессах и в других случаях. Современные самолеты и вертолеты снабжены гидравлическими системами, выполняющими многие ...

0 комментариев