Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях их можно получить аналитически

3.  Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях их можно получить аналитически.

4.  После выполнения первого этапа (условной оптимизации) приступают ко второму этапу — безусловной оптимизации.

а) Если начальное состояние  задано ,
то непосредственно определяют максимум целевой
функции

(3.5)

а затем — искомое безусловное оптимальное управление по цепочке

(3.6)

В этой цепочке переход, указанный сплошной линией, проводят по последовательности , а пунктирной — с помощью уравнений состояний.

б) Если задано множество  начальных состояний,
, то дополнительно решают еще одну задачу на максимум:

(3.7)

откуда находят , а затем, как и в п. а), по цепочке (3.6) —безусловное оптимальное управление.

Иногда на этапе условной оптимизации вычислительный процесс удобно строить в направлении, обратном описанному выше, т. е. от 1-го шага к л-му. Этот способ получил название прямого хода вычислений в отличие от вышеизложенного, который называется обратным ходом. Уравнения состояний для прямого хода удобно записывать в виде

(3.8)

Они могут быть получены решением уравнений (1.1) относительно . Введем в рассмотрение условные максимумы показателя эффективности за k шагов, от 1-го до k-го включительно — величины . Повторив рассуждения п. 2.2.2., придем к следующей форме уравнений Беллмана:

(3.9)

(3.10)

В результате решения этих уравнений получим последовательности

(3.11)

Этап безусловной оптимизации не отличается принципиально от аналогичного этапа в обратном ходе вычислений: , если  задано, или

(3.12)

если указано множество  возможных конечных состояний. Далее, определяем безусловное оптимальное управление по цепочке

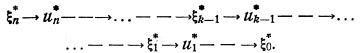(3.13)

2.2.4 Оптимальное распределение ресурсов

Класс задач, рассматриваемый в данной главе, имеет многочисленные практические приложения.

В общем виде эти задачи могут быть описаны следующим образом. Имеется некоторое количество ресурсов, под которыми можно понимать денежные средства, материальные ресурсы (например, сырье, полуфабрикаты, трудовые ресурсы, различные виды оборудования и т. п.). Эти ресурсы необходимо распределить между различными объектами их использования по отдельным промежуткам планового периода или по различным промежутками по различным объектам так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, товарная продукция, фондоотдача (задачи максимизации) или суммарные затраты, себестоимость, время выполнения данного объема работ и т. п. (задачи минимизации).

Вообще говоря, подавляющее число задач математического программирования вписывается в общую постановку задачи оптимального распределения ресурсов. Естественно, что при рассмотрении моделей и вычислительных схем решения подобных задач методом ДП необходимо конкретизировать общую форму задачи распределения ресурсов.

В дальнейшем будем предполагать, что условия, необходимые для построения модели ДП, в задаче выполняются. Опишем типичную задачу распределения ресурсов в общем виде.

Задача 1. Имеется начальное количество средств , которое необходимо распределить в течение п лет между s предприятиями. Средства  (k=1, 2,…,n; i=1,…, s), выделенные в k-м году i-му предприятию, приносят доход в размере  и к концу года возвращаются в количестве . В последующем распреелении доход может либо участвовать (частично или полностью), либо не участвовать.

Требуется определить такой способ распределения ресурсов (количество средств, выделяемых каждому предприятию в каждом плановом году), чтобы суммарный доход от s предприятий за п лет был максимальным.

Следовательно, в качестве показателя эффективности процесса распределения ресурсов за п лет принимается суммарный доход, полученный от s предприятий:

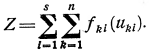(4.1)

Количество ресурсов в начале k-го года будем характеризовать величиной  (параметр состояния). Управление на k-м шаге состоит в выборе переменных   обозначающих ресурсы, выделяемые в k-м году i-му предприятию.

Если предположить, что доход в дальнейшем распределении не участвует, то уравнение состояния процесса имеет вид

(4.2)

Если же некоторая часть дохода участвует в дальнейшем распределении в каком-нибудь году, то к правой части равенства (4.2) прибавляется соответствующая величина.

Требуется определить ns неотрицательных переменных , удовлетворяющих условиям (4.2) и максимизирующих функцию (4.1).

Вычислительная процедура ДП начинается с введения функции , обозначающей доход, полученный за п—k+1 лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s предприятиями, если в k-м году распределялось средств. Функции  для k=1, 2, ...n-1 удовлетворяют функциональным уравнениям (2.2), которые запишутся в виде:

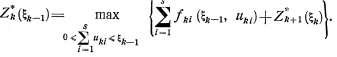(4.3)

При k=n согласно (2.2) получаем

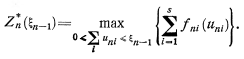(4.4)

Далее необходимо последовательно решить уравнения (4.4) и (4.3) для всех возможных  (k = n—1, п—2, 1). Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных. Таким образом, задача с ns переменными сведена к последовательности п задач, каждая из которых содержит s переменных. В этой общей постановке задача по-прежнему сложна (из-за многомерности) и упростить ее, рассматривая как ns-шаговую задачу, в данном случае нельзя. В самом деле, попробуем это сделать. Пронумеруем шаги по номерам предприятий сначала в 1-м году, затем во 2-м и т. д.:

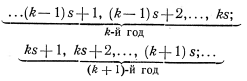
и будем пользоваться одним параметром  для характристики остатка средств.

В течение k-го года состояние ' к началу любого шага s(k-1)_+i (i=1,2,…,s) определится по предыдущему состоянию  с помощью простого уравнения . Однако по истечении года, т.е. к началу следующего года, к наличным средствам необходимо будет добавить 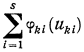средств и, следовательно, состояние  в начале (ks+1)-гo шага будет зависеть не только от предшествующего ks-гo состояния, но и от всех s состояний и управлений за прошлый год. В результате мы получим процесс с последействием. Чтобы исключить последействие, приходится вводить несколько параметров состояний; задача на каждом шаге остается по-прежнему сложной из-за многомерности.

Задача 2. Планируется деятельность двух предприятий (s=2) в течение п лет. Начальные средства составляют . Средства х, вложенные в предприятие I, приносят к концу года доход f₁(x) и возвращаются в размере  аналогично, средства х, вложенные в предприятие II, дают доход f₂(x) и возвращаются в размере . По истечении года все оставшиеся средства заново перераспределяются между предприятиями I и II, новых средств не поступает и доход в производство не вкладывается.

Требуется найти оптимальный способ распределения имеющихся средств.

Будем рассматривать процесс распределения средств как n-шаговый, в котором номер шага соответствует номеру года. Управляемая система — два предприятия с вложенными в них средствами. Система характеризуется одним параметром состояния  —количеством средств, которые следует перераспределить в начале k-гo года. Переменных управления на каждом шаге две:  — количество средств, выделенных соответственно предприятию I и II. Так как средства ежегодно перераспределяются полностью, то  ). Для каждого шага задача становится одномерной. Обозначим  через , тогда

Показатель эффективности k-гo шага равен  . Это — доход, полученный от двух предприятий в течение k-гo года.

Показатель эффективности задачи — доход, полученный от двух предприятий в течение п лет — составляет

(4.5)

Уравнение состояния выражает остаток средств  после k-гo шага и имеет вид

(4.6)

Пусть —условный оптимальный доход, полученный от распределения средств  между двумя предприятиями за n—k+1 лет, начиная с k-гo года до конца рассматриваемого периода. Запишем рекуррентные соотношения для этих функций:

(4.7)

где  - определяется из уравнения состояния (4.6).

При дискретном вложении ресурсов может возникнуть вопрос о выборе шага Δх в изменении переменных управления. Этот шаг может быть задан или определяется исходя из требуемой точности вычислений и точности исходных данных. В общем случае эта задача сложна, требует интерполирования по таблицам  на предыдущих шагах вычисления. Иногда предварительный анализ уравнения состояния позволяет выбрать подходящий шаг Δх, а также установить предельные значения , для которых на каждом шаге нужно выполнить табулирование.

Рассмотрим двумерную задачу, аналогичную предыдущей, в которой строится дискретная модель ДП процесса распределения ресурсов.

Задача 3. Составить оптимальный план ежегодного распределения средств между двумя предприятиями в течение трехлетнего планового периода при следующихусловиях:

1) начальная сумма составляет 400;

2) вложенные средства в размере х приносят на предприятии I доход f₁(x) и возвращаются в размере 60% от х, а на предприятии II — соответственно f2(x) и 20%;

3) ежегодно распределяются все наличные средства, получаемые из возвращенных средств:

4) функции f₁(x) и f2(x)заданы в табл. 1:

Модель динамического программирования данной задачи аналогична модели, составленной в задаче 1.

Процесс управления является трехшаговым. Параметр  — средства, подлежащие распределению в k-м году (k=l, 2, 3). Переменная управления  — средства, вложенные в предприятие I в k-м году. Средства, вложенные в предприятие II в k-м году, составляют  Следовательно, процесс управления на k-м шаге зависит от одного параметра  (модель одномерная). Уравнение состояния запишется в виде

(4.8)

А функциональные уравнения в виде

(4.9)

(4.10)

Попытаемся определить максимально возможные значения, для которых необходимо проводить табулирование на k-м шаге (k=l, 2, 3). При =400 из уравнения (4.8) определяем максимально возможное значение  имеем  = 0,6*400=2400 (все средства вкладываются в предприятие I). Аналогично, для  получаем предельное значение 0,6*240 = 144. Пусть интервал изменения  совпадает с табличным, т. е. Δх =50. Составим таблицу суммарной прибыли на данном шаге:

Это облегчит дальнейшие расчеты. Так как  то клетки, расположенные по диагонали таблицы, отвечают одному и тому же значению , указанному в 1-й строке (в 1-м столбце) табл. 2. Во 2-й строке таблицы записаны значения f₁(x), а во 2-м столбце — значения f₂(у)взятые из табл. 1.Значения в остальных клетках таблицы получены сложением чисел f₁(x) и f₂(у),стоящих во 2-й строке и во 2-м столбце и соответствующих столбцу и строке, на пересечении которых находится данная клетка. Например, для =150 получаем ряд чисел: 20 —для х = 0, у=150; 18 —для х=50, у=100; 18— для х—100, у=50; 15 — для х= 150, у=0.

Проведем условную оптимизацию по обычной схеме. 3-й шаг. Основное уравнение (4.9)

Как указывалось выше, . Просмотрим числа на диагоналях, соответствующих =0; 50; 100; 150 и на каждой диагонали выберем наибольшее. Это и есть  В 1-й строке находим соответствующее условное оптимальное управление. Данные оптимизации на 3-м шаге поместим в основную таблицу (табл. 4). В ней введен столбец Δх, который в дальнейшем используется при интерполяции.

Оптимизация 2-го шага проведена в табл. 5 согласно уравнению вида (4.10):

При этом может быть получен максимальный доход, равный Zmax=99,l. Прямой подсчет дохода по табл. 2 для найденного оптимального управления дает 97,2. Расхождение в результатах на 1,9 (около 2%) объясняется ошибкой линейной интерполяции.

Мы рассмотрели несколько вариантов задачи оптимального распределения ресурсов. Существуют другие варианты этой задачи, особенности которых учитываются соответствующей динамической моделью.

2.2.5 Оптимальное управление запасами

Класс задач, в которых рассматривается оптимальное управление Запасами, является наиболее характерным для динамического программирования. Это обусловлено тем, что в задачах управления запасами процесс естественно разворачивается во времени, причем управление как раз и заключается в том, что решение на данном промежутке времени принимается с учетом того состояния, к которому пришла система за предшествующие периоды времени. Кроме того, эти задачи связаны, как правило, с дискретным характером переменных и, следовательно, решаются довольно сложно другими методами. Наконец, весьма важным обстоятельством является то, что форма зависимостей задачи для каждого периода времени является довольно простой (часто — линейной), что облегчает решение частной задачи оптимизации на каждом шаге, в то время как единовременное решение общей задачи с большим числом переменных (для многих промежутков времени и кусочно-линейной или нелинейной целевой функцией для всего процесса) является достаточно сложным.

Проблема управления запасами является одной из важнейших областей практического приложения экономико-математических методов, в том числе методов математического программирования. Мы ограничимся анализом некоторых простейших задач с целью иллюстрации их решения методами динамического программирования.

При формулировке задач управления запасами используют такие понятия.

Запасы — это любые денежные или материальные ценности, которые периодически пополняются (производятся, доставляются и т. д.) и некоторое время сохраняются с целью расходования их в последующие промежутки времени. Уровень запасов в любой момент времени определяется начальным уровнем запасов плюс пополнение и минус расход за промежуток времени от начального момента до данного.

Управление запасами в общем случае состоит в воздействии на соотношение между двумя основными факторами— пополнением и расходом. Цель управления — оптимизация некоторого критерия, зависящего от расходов на хранение запасов, стоимости поставок, затрат, связанных с пополнением, штрафов и т. д.

В такой общей постановке подобные задачи могут иметь самое разнообразное практическое применение. Например, под запасами можно понимать продукцию предприятия, которая производится непрерывно (пополнение) и отгружается потребителям определенными дискретными партиями (расход). При этом спрос на продукцию предполагается наперед заданным (детерминированный спрос) или подверженным случайным колебаниям (стохастическая задача). Управление запасами состоит в определении, размеров необходимого выпуска продукции для удовлетворения заданного спроса. Цель — минимизация суммарных затрат на хранение и пополнение запасов. Под запасами можно понимать запасы сырья или других материалов, поставляемых дискретными партиями (пополнение) и должных обеспечить непрерывное потребление в процессе производства (расход). Критерием оптимальности могут служить суммарные затраты на хранение запасов, замораживание оборотных средств и поставки запасов.

Запасами могут быть товары, поставляемые в магазин определенными партиями и предназначенные для удовлетворения непрерывного, но подверженного случайным колебаниям покупательского спроса. Критерий оптимальности — суммарные затраты на поставки, хранение запасов и изменение производственного ритма в связи с вариациями спроса.

Запасами могут быть и сезонные товары, сохраняющиеся на складе ограниченной емкости. Товары можно покупать и продавать в различных количествах по ценам, меняющимся во времени. Задача состоит в определении политики покупок и продаж, обеспечивающих максимум суммарной прибыли, и является примером задачи складирования.

Число таких примеров можно было бы умножить. Однако в настоящем параграфе мы рассмотрим лишь некоторые простейшие динамические модели задач управления запасами.

Если в задаче исходные данные определены однозначно, то задачи называются детерминированными; если же хотя бы часть данных носит случайный характер и заданы распределения вероятностей, то соответствующие задачи называются стохастическими. В этой главе мы ограничимся примерами детерминированных задач управления запасами.

Рассмотрим модель задачи управления запасами при заданном расходе. Управление в этих задачах будет сводиться к пополнению.

Задача 1. Планируемый период разделен на n промежутков времени (дни, месяцы, кварталы и т. д.), в которых задан расход d_k (k=l, 2, ..., п), производимый в конце каждого из промежутков. Известны начальный уровень запасов и зависимость суммарных затрат на хранение и пополнение запасов в данном периоде от среднего уровня хранимых запасов и их пополнения.

Требуется определить размеры пополнения запасов в каждом промежутке времени для удовлетворения заданного расхода из условия минимизации суммарных затрат за весь планируемый период времени.

Составим математическую модель задачи. Обозначим размер пополнения запасов в k-м промежутке времени через x_k, а уровень запасов в начале этого промежутка (после произведенного расхода) — через -Согласно условию, суммарные затраты в k-м промежутке зависят от x_k и  — среднего уровня запасов в k-м промежутке, равного

(5.1)

Следовательно, затраты в k-м промежутке можно рассматривать как функцию

Целевая функция задачи — суммарные затраты — запишется в виде

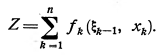(5.2)

Требуется определить переменные x_k, которые связаны с переменными  балансовыми уравнениями

(5.3)

выражающими уровень запаса в начале (k+1)-гo промежутка через сумму уровня запасов в начале k-гo промежутка и пополнения запасов в этом промежутке x_k минус расход d_k.

Ставится задача — найти совокупность п переменных x_k, удовлетворяющих ограничениям (5.3) — (5.5) и минимизирующих функцию (5.2).

Подобные задачи при большом числе переменных и нелинейности функций  другими методами математического программирования решаются сложно. Особенно сложным становится решение, когда на переменные x_k налагаются условия целочисленности (или в общем случае — дискретности), как это часто бывает.

Дадим описание динамической модели задачи. Будем рассматривать n-шаговый процесс оптимизации с параметрами состояния  и переменными управлениями x_k. Тогда равенство (5.3) представляет собой уравнение состояния. Здесь удобнее использовать прямую схему расчета, так как задано конечное состояние.

В задачах управления запасами чаще всего возникает именно такая ситуация, поэтому продемонстрируем построение прямой схемы вычислений.

Обозначим через ) условные оптимальные затраты за промежутки, начиная с 1-го до k-гo включительно, если в конце k-гo промежутка уровень запасов равен .

Начинаем с условной оптимизации 1-го шага в предположении, что к концу этого шага система окажется в состоянии

(5.6)

На k-м шаге получим соответственно

(5.7)

В соответствии с формой рекуррентных соотношений удобно и уравнение состояния (5.3) записать в виде

(5.8)

При решении локальных задач в соответствии с уравнениями (5.6) и (5.7) будем считать, что состояние  в конце шага известно. Поэтому и неравенство (5.4) удобно записать для т. е. в виде , откуда следуют ограничения на x_h:

(5.9)

Функцию затрат также удобно привести к зависимости от состояния в конце шага, используя уравнение (5.8):

Выполнив условную оптимизацию, получим последовательно

Далее (безусловная оптимизация), находим Z_max = при заданном конечном состоянии, или Z_max = и , если конечное состояние не задано. Затем последовательно определяем

Данная задача является примером общего случая, когда функции ) — затраты на производство и  — затраты на хранение — являются вогнутыми (Функция f(x), определенная в промежутке X, называется вогнутой, если для любых точек x₁X, x₂X (x₁x₂) выполняется неравенство f(t₁x₁+t₂x₂)≥t₁f(x₁)+t₂f(x₂) при любых t₁≥0, t₂≥0 таких, что t₁+t₂=1). Тогда суммарные затраты  и целевая функция  также вогнутые функции от переменных

Если  общая сумма затрат, то вогнутость функций Z означает, что каждая дополнительная единица продукции (производимая, хранимая) стоит не больше предыдущей. Подобная ситуация чаще всего встречается в производстве.

Модель задачи с вогнутыми функциями затрат на производство и хранение называется динамической моделью экономически выгодного размера партии .

Вогнутость функции производственных затрат встречается, например, в случае, если выпуск продукции связан с затратами на дополнительную операцию, переналадку оборудования или освоение нового оборудования. После этой подготовительной стадии процесса производства (больших единовременных затрат) выпуску каждой дополнительной единицы продукции соответствуют не меняющиеся пропорциональные затраты.

Другим примером может служить модель задачи пополнения запасов у внешнего поставщика, который нередко делает скидки в зависимости от размера закупаемой партии, назначает ступенчатые цены.

Например, функция

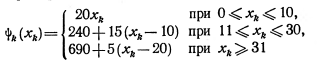
является вогнутой, так как коэффициент при x_h убывает с ростом x_h

Известно, что глобальный минимум вогнутой функции достигается по крайней мере в одной из угловых точек области. В рассмотренном выше случае область задана системой п линейных уравнений (5.3). и условиями неотрицательности (5.4) и (5.5). Угловым точкам области соответствуют опорные решения системы (5.3); в каждом из которых не более чем п переменных x_k и положительны, а остальные равны нулю. Предположим, что все . Тогда, при любом k, если , то , а если , то , иначе нечем будет обеспечить расход d_k к концу k-гo периода. Одновременно невозможно, чтобы , так как при этом в опорном решении системы (5.3) оказалось бы более чем п положительных составляющих.

Из уравнения состояния (5.8) получим

При проведении условной оптимизации на k-м шаге согласно уравнению (5.7) достаточно сравнить и выбрать наименьшее из двух значений в указанных двух точках, которые принимает выражение, содержащееся в фигурных скобках:

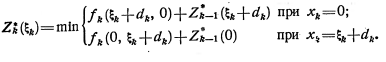
Для 1-го шага (k=1) имеем  и, следовательно,

Оптимальное управление пополнением запасов x_k на любом k-м шаге имеет следующий вид:

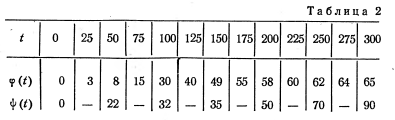
Задача 2. Определить оптимальное пополнение запасов в течение четырех периодов при следующих условиях:  пополнение запасов может производиться партиями, кратными 50; функции затрат на хранение  и на пополнение , одинаковые для всех периодов времени, заданы в табл. 2:

Задача носит дискретный характер. Для упрощения, поскольку расход и пополнение кратны 50, расчеты будем вести в целых партиях. Таким образом, d₁ = 3, d₂=l, d₃ = 2, d₄ = 2, переменные x_h и параметры  меняются с шагом в единицу. Вычисления выполняем в соответствии с моделью, приведенной в задаче 1. Как обычно, при выполнении первого этапа расчеты производим в таблицах: основной (табл. 3) и вспомогательных (табл. 4—7).

Для 1-го шага имеем единственное значение  . Поэтому

Прежде чем перейти к табулированию, определим предельные значения для параметров состояния. Так как , то даже при  должно быть , следовательно, . Соответственно

В заключение настоящей главы рассмотрим тип задач, названных выше задачами складирования.

Особенностью этих задач является наличие двух переменных управления (двумерная модель). Однако решение этих задач значительно упрощается благодаря линейности целевой функции.

Задача 3. Емкость склада по хранению запасов ограничена некоторой величиной с. В каждом из п промежутков времени запасы могут пополняться с затратами  на единицу продукции и расходоваться с получением дохода  за единицу продукции, причем решение о пополнении или расходовании запасов принимается однократно в каждом промежутке времени. Определить оптимальную стратегию в управлении запасами из условия максимизации суммарной прибыли при заданном начальном уровне запасов.

Уточним постановку задачи. Возможны три варианта в очередности пополнения и расходования запасов в каждом из промежутков времени: I вариант — пополнение предшествует расходу; II вариант — расход предшествует пополнению и III вариант — очередность любая.

В III варианте выбор оптимальной стратегии означает не только определение размера пополнения и расхода, но и выбор оптимальной очередности в каждом из промежутков времени.

Указанные варианты условия отразятся на форме ограничений модели задачи.

Составим динамическую модель задачи. Рассмотрим n-шаговый процесс, понимая под k-м шагом промежуток времени, в котором принимается решение о пополнении или расходовании запасов (k = 1, 2,..., п).

В качестве параметров состояния  примем запас товаров в начале k-гo шага. Переменными управления служат размеры пополнения (х_к) и расхода (у_к) запасов на k-м шаге. Тогда уравнение состояния, выражающее материальный баланс запасов, запишется в виде

(5.11)

Будем решать задачу с помощью обратной вычислительной схемы, т. е. используя рекуррентные соотношения в виде

(5.12)

(5.13)

Переменные задачи должны удовлетворять условиям неотрицательности:

(5.14)

и дополнительным ограничениям для всех k, зависящих от варианта постановки задачи:

(5.15)

(5.15’)

III вариант: или (5.15), или (5.15').

Первые неравенства в (5.15) и (5.15') диктуются ограниченной емкостью склада, вторые — условием, согласно которому расход не может превышать наличные запасы. Для III варианта альтернативные условия означают, что если будет принято решение сначала пополнить запасы, а затем их расходовать, то должны выполняться условия (5.15); если же будет принят противоположный порядок, то должны выполняться условия (5.15').

Решение задач условной максимизации по двум переменным согласно рекуррентным соотношениям (5.12) и (5.13) в общем случае представляет собой сложную задачу, однако линейность функций

и  

максимумы которых определяются на каждом шаге, а также ограничений, налагаемых на переменные, позволяет значительно упростить решение всех этих частных задач.

Рассмотрим подробнее решение задачи в I варианте постановки. Ограничения (5.14) и (5.15) определяют при данном значении параметра  область допустимых значений Х_k и Ук в виде выпуклого четырехугольника ABCD, изображенную на рис. 6. Так как в этой области максимизируется линейная функция, то получается задача линейного программирования, оптимальное решение которой достигается, по крайней мере, в одной из вершин области. На рис. 6 находим координаты всех четырех вершин:  . Поэтому вместо нахождения максимума по соотношениям (3.12) и (3.13) при произвольных изменениях достаточно вычислить значения выражений, содержащихся в фигурных скобках, во всех четырех вершинах и путем сравнения выбрать среди них наибольшее.

При этом для последнего (n-го) шага можно ограничиться выбором из двух альтернатив, так как значение  в точках А и D дает заведомо меньшее число, чем соответственно в точках В ч С.

Итак, для n-го шага получаем

(5.12’)

Для выполнения оптимизации на последующих шагах предварительно найдем из уравнения (5.11) значение  для каждой точки. Тогда получим:  в точке А;  в точке в точке  в точке D. Вместо соотношения (5.13) получаем

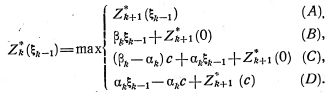(5.13’)

При выполнении практических расчетов оказывается достаточным не табулировать функции  Для всех значений , а ограничиться вычислением этих функций лишь для крайних значений  т. е. для  

В случае II варианта исходной постановки задачи получим область, изображенную на рис. 7. В новой области изменятся лишь координаты вершины С; находим . Аналогично предыдущему получим следующие формулы для выполнения условной максимизации:

(5.12’’)

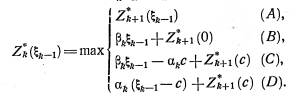(5.13’’)

Наконец, при III варианте постановки задачи на каждом шаге мы должны выбрать наибольшее число по формулам (3.12'), (3.13') и сравнить его с наибольшим числом, найденным по формулам (3.12"), (3.13"). Сопоставив полученные таким образом два значения  выбираем из них наибольшее. Это и есть окончательное выражение для  Одновременно, в зависимости от того, к какому из вариантов относится найденный максимум, устанавливается выгодная на данном шаге очередность пополнения и расхода запасов.

Поскольку выражение (3.12") содержится среди альтернатив выбора по формуле (3.12'), для k-го шага достаточно производить выбор только по соотношению (3.12').

Аналогично, так как среди четырех альтернатив в формуле (3.13") только третья альтернатива отличается от выбираемых по формуле (3.13'), то достаточно производить выбор по формуле (3.13'), добавив пятую альтернативу.

2.2.6 Задача о замене

Одной из важных экономических проблем, с которыми приходится встречаться на практике, является определение оптимальной стратегии в замене старых станков, производственных зданий, агрегатов, машин и т. д., другими словами, старого оборудования — на новое.

Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на его ремонт и обслуживание, а вместе с тем снижаются производительность и так называемая ликвидная стоимость.

Наступает момент, когда старое оборудование более выгодно продать, заменить новым, чем эксплуатировать ценой больших затрат. При этом оборудование можно заменить либо новым оборудованием того же вида, либо новым, более совершенным в техническом отношении, с учетом технического прогресса.

Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при определении сроков замены может служить либо прибыль от эксплуатации оборудования, которую следует максимизировать, либо суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации. Известно, что при заданном плане выпуска продукции максимизация прибыли эквивалентна минимизации затрат. Практически удобнее пользоваться вторым критерием, вводя для учета снижения производительности условно приведенные затраты.

Условимся считать, что решения о замене оборудования принимаются периодически в начале каждого промежутка (года, месяца, недели и т. д.), на которые разбит плановый период. Предположим также, что оборудование может использоваться неограниченно долго, если тратить достаточные суммы на его ремонт.

Основной характеристикой оборудования является его возраст. От возраста оборудования зависят эксплуатационные расходы, затраты на производство, производительность и ликвидная стоимость. Эти показатели изменяются, если учитывать технический прогресс, не только при замене старого оборудования новым, с новыми технико-экономическими характеристиками, но и новым того же типа, еще не использованным. В последнем случае изменение вызвано моральным износом.

Метод ДП обеспечивает единый подход к решению всех видов задач о замене.

При составлении модели ДП мы рассматриваем процесс замены как n-шаговый, разбив весь плановый период на п промежутков. Так как в начале каждого из этих промежутков принимается решение либо о сохранении оборудования, либо о его замене, то управление на k-м шаге (k=l, ..., п) содержит всего лишь две альтернативные переменные. Обозначим через и^с решение, состоящее в сохранении старого оборудования, а через и³ — решение, состоящее в замене старого оборудования новым. Функциональные уравнения, благодаря наличию двух альтернативных управлений на каждом шаге, содержат лишь две величины: одна выражает условную прибыль (условные затраты) при управлении u^с, другая — тот же показатель при управлении и^з. Условная оптимизация на каждом шаге состоит в вычислении двух величин и в выборе из них наибольшей (наименьшей). Это значительно упрощает расчеты на стадии условной оптимизации и позволяет решать вручную задачи о замене с большим числом шагов.

Рассмотрим две модели ДП задачи о замене оборудования. В одной из них в качестве показателя эффективности выберем прибыль, которую следует максимизировать, в другой — суммарные затраты на эксплуатацию, которые следует минимизировать.

Задача 1. Определить оптимальные сроки замены оборудования в течение п лет, при которых прибыль от эксплуатации оборудования максимальна, если известны: р — начальная стоимость оборудования; f(t) —стоимость производимой продукции на оборудовании возраста t лет; r(t) —ежегодные затраты на эксплуатацию оборудования возраста t лет; —ликвидная стоимость оборудования возраста t лет. .

Рассмотрим n-шаговый процесс, считая k-м шагом номер k-гo года от начала эксплуатации (k=l, 2, ..., п). Выше указывалось, что управление на k-м шаге выбирается из двух возможных решений: u^с — сохранить и продолжать использование старого оборудования или и³ — заменить оборудование новым.

Будем считать, что в начале планового периода возраст оборудования равен t₀. Состояние  -системы (оборудования) в начале k-ro шага характеризуется одним параметром  — возрастом оборудования. Для k-ro шага параметр состояния t может принимать значения 0,1, 2, ..., k—1, т. е. t≤k-1

Если к началу k-гo шага система находилась в состоянии , то под влиянием управления и^с в конце k-гo шага она перейдет в состояние  возраст оборудования увеличится на один год. Под влиянием управления и³, принятого на k-м шаге, система перейдет в состояние  (замену произвели в начале k-гo года; в конце k-го года возраст нового оборудования равен одному году).

Уравнение состояния (1.2) для данного процесса имеет вид

(6.1)

Определим прибыль на k-м шаге (показатель эффективности k-гo шага), соответствующую каждому из альтернативных управлений и^с и и³. Выбирая на k-м шаге управление и^с, мы сможем произвести продукции стоимостью f(t) на старом оборудовании, что потребует затрат r(t), поэтому прибыль равна f(t)—r(t). Обозначим ее через

(6.2)

При управлении и³ получим доход  от продажи старого оборудования (ликвидную стоимость) и f(0) от произведенной на новом оборудовании продукции, затратив р на приобретение нового оборудования и r(0) на содержание нового оборудования. В этом случае прибыль (обозначим ее через ) составляет

(6.3)

Построим обратную вычислительную схему решения данной задачи методом ДП.

Обозначим через  условную максимальную прибыль, полученную за n—k+l шагов использования оборудования с k-гo по n-й шаг включительно, если к k-му шагу возраст оборудования составлял  лет, при условии, что был выбран оптимальный режим эксплуатации. Соответствующее условное оптимальное управление на k-м шаге обозначим через . Условный максимальный доход за последний n-й промежуток составляет

(6.4)

Сравнив эти две величины для всех возможных значений t<n получим значения  и соответствующие значения . Предположим, что для всех значений  известна максимальная прибыль, полученная за n—k шагов с (k+1)-гo по n-й включительно. Поэтому основные рекуррентные соотношения можно записать в виде

(6.5)

В уравнении (6.5) величина —условная максимальная прибыль, полученная за n—k шагов, если к началу (k+l)-гo шага система находилась в состоянии  (возраст оборудования составлял один год).

•Процесс условной оптимизации на каждом шаге, начиная с n-го, сводится к сравнению двух величин в уравнениях (6.4) и (6.5) и выбору наибольшей из них. Этап условной оптимизации заканчивается, как обычно, получением последовательностей функций

На этапе безусловной оптимизации для  (возраст оборудования в начале процесса) получаем  , а далее по цепочке: , из (6.1) находим ,, откуда , и т. д. Оптимальное управление  представляет собой набор управлений u^с и и³.

Замечание. В задаче 1 не рассматривался вопрос о том, что происходит с оборудованием после п лет его эксплуатации. Можно предположить, что п неограниченно велико и, рассматривая процесс для достаточно большого значения п, получить закономерность в оптимальном управлении в виде периодически повторяющихся циклов замены и использования старого оборудования, (такой пример будет рассмотрен ниже). Можно также предположить, что после л лет использования оборудование продается и ликвидная стоимость присоединяется к общей прибыли. Во втором случае уравнения (6.4) принимают вид

(6.6)

Рассмотрим некоторую модификацию задачи 1.

Задача 2. В задаче 1 предположим, что ежегодные затраты на эксплуатацию, ликвидная и начальная стоимость зависят не только от возраста оборудования t, но и от времени, прошедшего с начала процесса. Пусть r_h{t)—затраты на эксплуатацию в течение k-гo года, если со времени последней замены прошло t лет; —ликвидная стоимость оборудования возрастав лет, если оно продается в начале k-гo года; р_k — начальная стоимость оборудования, если оно куплено в начале k-гo года.

Требуется определить оптимальные сроки замены старого оборудования новым в течение п лет с тем, чтобы минимизировать затраты на его содержание.

Показатель эффективности в данной задаче — суммарные затраты на эксплуатацию оборудования. Затраты на k-м шаге, как и прежде, зависят от выбранного управления. При управлении и_k= и^с эти затраты равны , а при управлении и_k =u³ составляют  

Пусть Z_k*{t)—условные минимальные затраты за n—k+1 шагов с k-гo по n-й включительно, если к началу k-гo шага возраст оборудования составлял t лет, при условии, что был выбран оптимальный режим эксплуатации.

Рекуррентные соотношения для Z_k*{t) имеют вид

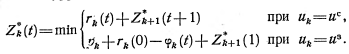(6.7)

Для n-го шага соответственно получим

(6.8)

Вычислительный процесс строится как и в предыдущей задаче.

Введение в условие задачи функций, оценивающих затраты, выпуск продукции и стоимость, зависящие не только от возраста t, но и непосредственно от k, т. е. от времени, прошедшего с начала процесса, является косвенным способом учета технического прогресса.

Как уже отмечалось неоднократно, модели ДП очень гибки и в смысле возможностей анализа чувствительности к вариации исходных данных, и в смысле возможностей включения в модель различных модификаций задачи. Так, например, аналогичная модель может быть построена для задач, в которых ежегодно рассматривается более двух вариантов управления («сохранение», «замена», «реконструкция» и т. д.). Можно рассматривать задачи, в которых затраты или прибыль зависят не только от возраста оборудования, но и еще от одного параметра, например, времени, прошедшего после восстановительного ремонта, и т. д.

Замечание. Если функции затрат, ликвидная и начальная стоимости в задаче 2 зависят от времени τ, прошедшего с начала эксплуатационного периода, и τ не совпадает с k, то состояние системы следует характеризовать двумя параметрами τ и t.

В заключение главы рассмотрим задачу определения оптимальной стратегии замены оборудования при бесконечном плановом периоде.

Задача 3. Определить оптимальные сроки замены оборудования при неограниченном времени его использования, если известны: р — начальная стоимость; r(t) — эксплуатационные затраты на содержание оборудования возраста t лет в течение ближайшего года;  —ликвидная стоимость оборудования возраста t лет.

В задаче будем минимизировать затраты. Параметр состояния есть время: . Процесс, является бесконечным, поэтому условные минимальные затраты  за все последующее время, начиная с k-гo года, зависят только от  и не зависят от k.

При рассмотрении бесконечного процесса необходимо ввести так называемый дисконтирующий множитель 0<α<1, позволяющий привести сумму в последующий момент времени к настоящему моменту с учетом ежегодного роста по правилу сложных процентов. Если имеется первоначальная сумма а руб., то через п лет она составит, при процентной ставке р%, сумму  руб. Наоборот, конечную сумму а руб. через п лет можно получить от первоначальной суммы руб. Множитель называется коэффициентом дисконтирования.

Учитывая этот множитель и повторяя весь ход рассуждений, изложенный в предыдущих задачах, получим следующие функциональные уравнения:

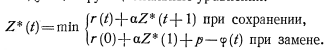(6.9)

Поскольку конечного шага нет, обратный ход выпол-. нить нельзя, поэтому решим уравнения явно следующим образом.

Для 1-го шага имеем , поэтому

Так как  то выражение, стоящее в первой строке, всегда не больше выражения во второй строке. Поэтому , что соответствует сохранению оборудования.

Пусть оптимальным является решение о сохранении для первых N шагов и о замене на (N+1)-м шаге. Задача состоит в определении этого числа N. Запишем последовательность рекуррентных соотношений для этих N шагов:

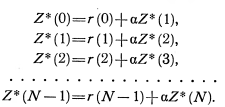
Исключив из этих равенств последовательно Z*(2),Z*(3), … получим

(6.10)

Но для (N+ 1)-го шага по предположению оптимальным является решение о замене оборудования, следовательно,

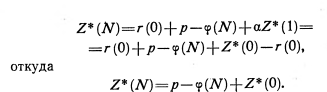
Подставляя значение Z*(N) в равенство (6.10) и разрешая полученное при этом уравнение относительно Z*(0), найдем

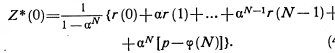(6.11)

Величина Z*(0) равна необходимому минимуму затрат на весь процесс. Теперь, полагая последовательно N = 1, 2, 3, .... вычисляем значение Z*(0) и находим среди них наименьшее.

  Заключение

В данной курсовой работе рассмотрены виды математических моделей, используемых в экономике и менеджменте, а также их классификация.

Особое внимание в курсовой работе уделено оптимизационному моделированию.

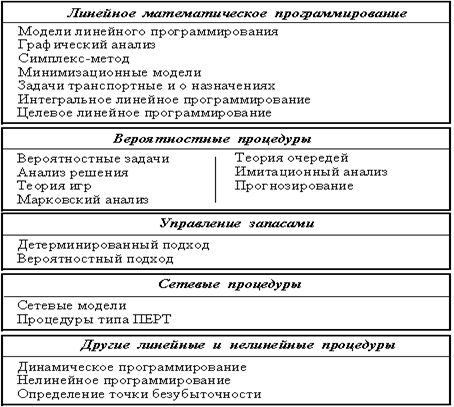
Изучен принцип построения моделей линейного программирования, также приведены модели следующих задач:

·  Задача о раскрое материалов;

·  Задача выбора оптимальной производственной программы предприятия;

·  Задача о диете;

·  Транспортная задача.

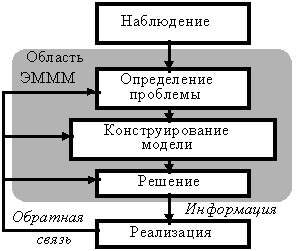
В работе представлены общие характеристики задач дискретного программирования, описан принцип оптимальности и уравнение Беллмана, приведено общее описание процесса моделирования.

Для построения моделей выбраны три задачи:

·  Задача оптимального распределения ресурсов;

·  Задача об оптимальном управлении запасами;

·  Задача о замене.

В свою очередь для каждой из задач построены различные модели динамического программирования. Для отдельных задач приведены числовые расчеты, в соответствии с построенными моделями.

Список литературы:

1.  Вавилов В.А., Змеев О.А., Змеева Е.Е. Электронное пособие “Исследование операций”

2.  Калихман И.Л., Войтенко М.А. “Динамическое программирование в примерах и задачах”, Москва ”Высшая школа”, 1979

3.  Косоруков О.А., Мищенко А.В. “Исследование операций”, Москва, 2003

4.  Материалы из сети Internet.