Навигация
Построение кода с заданной коррекцией
1.1.4 Построение кода с заданной коррекцией
При рассмотрении корректирующих кодов предполагалось, что его длина n задана, а повышение корректирующей способности кода достигалось за счёт уменьшения множества Nk разрешённых комбинаций при неизменном n или уменьшении информационных символов k. На практике коды строятся в обратном порядке: вначале выбирается количество информационных символов, а затем обеспечивается необходимая корректирующая способность кода за счёт добавления избыточных символов.
Если задано число корректирующих разрядов k (), а всего в коде n разрядов, то граница Хемминга для исправления l ошибок определяется выражением:
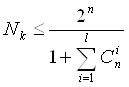 (6)
(6)
Все корректирующие коды можно разделить на два основных класса: непрерывные (рекуррентные) и блочные. В непрерывных кодах процесс кодирования и декодирование имеет непрерывный характер. Каждый избыточный символ (проверочный) формируется по двум или нескольким информационным символам. Проверочные символы размещаются в определённом порядке между информационными символами исходной последовательности.
В блочных кодах каждому сообщению (или элементу сообщения) соответствует кодовая комбинация из n символов, которая называется блоком. Блоки кодируются и декодируются раздельно. Блочные коды могут быть равномерными, если n – постоянно, и неравномерными, если n – непостоянно. Как непрерывные, так и блочные коды в зависимости от методов размещения проверочных символов могут быть разделимыми и неразделимыми. В разделимых кодах одни символы являются информационными, а другие проверочными и служат для обнаружения и исправления ошибок. Информационные и проверочные символы занимают во всех комбинациях одни и те же позиции.
Разделимые блочные коды называют n,k‑кодами, где n – значность кода, к – число информационных символов. Разделимые блочные коды делятся на несистематические и систематические. В несистематических кодах проверочные символы представляют суммы подблоков длиной l, на которые разделена последовательность информационных символов. Такой код может обнаружить серийные ошибки с длиной серии не более l. В несистематических или линейных кодах проверочные символы определяются в результате линейных операций над определёнными информационными символами. Для двоичных кодов каждый проверочный символ выбирается таким, чтобы его сумма по mod2 с определёнными информационными символами стала равной 0. При декодировании производится проверка на четность определённых групп символов, поэтому также коды ещё называют – коды с проверкой на четность.
1.1.5 Коды Хэмминга
Двоичный код Хэмминга содержит k информационных символов и p=n‑k избыточных символов. Избыточная часть кода строится так, чтобы при декодировании можно было указать номер позиции, в которой произошла ошибка. Это достигается путём многократной проверки принятой комбинации на четность. Количество проверок равно количеству избыточных символов Р. При каждой проверке получают двоичный контрольный символ. Если результат проверки даёт чётное число единиц, то контрольному символу присваивается 0, иначе –1. В результате всех проверок получается p‑разрядное двоичное число, указывающее номер искажённого символа. Для исправления ошибки достаточно проинвертировать данный символ.
Необходимое количество проверочных символов p (или значность кода n) определяется по формуле:
Nk £ 2n/(1+n)(7)
Значения проверочных символов и номера их позиций устанавливаются одновременно с выбором контролируемых групп кодовой комбинации.
При первой проверке получают цифру младшего разряда контрольного числа, указывающего номер искаженного символа. Если в результате проверки младший разряд контрольного числа равен 1, то один из символов данной группы искажён.
Для упрощения операций кодирования и декодирования рекомендуется размещать проверочные символы так, чтобы каждый входил в минимальное число проверяемых групп, то есть размещать контрольные символы на позициях, номера которых встречаются только в одной из проверочных групп: 1, 2, 4, 8.(Таблица 2). Следовательно в кодовой комбинации символы а1, а2, а4, а8 . . . должны быть проверочными, а символы а3, а5, а6, а7, а9, и т. д.- информационными.
Так как значения информационных символов определяются заранее, то значения проверочных символов должны быть такими, чтобы сумма единиц в каждой проверочной группе была чётным числом.
1.1.6 Циклические коды
Циклические коды являются наиболее простыми и эффективными для обнаружения и исправления независимых и серийных ошибок. Основным свойством циклических кодов является то, что каждая кодовая комбинация может быть получена путём циклической перестановки символов комбинации, принадлежащей данному коду, то есть если кодовый вектор V=(a0,a1,a2, . . ., an-2) принадлежит циклическому коду, то и вектор V1 = (an‑1, a0, a1, a2, . . ., an-2) также ему принадлежит. Циклические коды записываются в виде полиномов.
Идея построения циклических кодов базируется на использовании неприводимых многочленов. Неприводимым называется многочлен, который не может быть представлен в виде произведения многочленов низших степеней, т.е. такой многочлен делиться только на самого себя или на единицу и не делиться ни на какой другой многочлен. На такой многочлен делиться без остатка двучлен xn+1. Неприводимые многочлены в теории циклических кодов играют роль образующих полиномов.
Для построения циклического кода, комбинация простого k-значного кода Q(x) умножается на одночлен xr, затем делится на образующий полином P(x), степень которого равна r. В результате умножения Q(x) на xr степень каждого одночлена, входящего в Q(x), повышается на r. При делении произведения xrQ(x) на образующий полином получается частное C(x) такой же степени, как и Q(x). Частное C(x) имеет такую же степень, как и кодовая комбинация Q(x) простого кода, поэтому C(x) является кодовой комбинацией этого же простого k-значного кода. Наибольшее число разрядов остатка R(x) не превышает числа r. Окончательное выражение для кода:
F(x) = C(x) P(x) = Q(x) xr + R(x). (8)
Похожие работы
... взаимной нестабильности несущей частоты излучаемого сигнала и частоты настройки приемника и доплеровского сдвига. 2.2 Расчет энергетических характеристик Качество выделения информации приемным устройством цифровой системы передачи информации, связано с вероятностью ошибки приёма разряда сообщения. Связь между допустимым значением вероятности ошибки Рд и пороговым отношением мощности сигнала к ...
... сигналу дорівнює добутку ширини спектра сигналу на його тривалість і визначається [9] (1.6.1), де B – база сигналу. 2. Аналіз відомих технічних рішень побудови радіоприймального пристрою цифрової системи передачі інформації Структурна схема приймача в значній мірі визначається його призначенням, і видом модуляції сигналу. В структурному відношенні всі існуючі приймачі можна розділити на ...
... универсальный сервер часто называют сервером приложений. Серверы в сети часто специализируются. Специализированные серверы используются для устранения наиболее "узких" мест в работе сети: создание и управление базами данных и архивами данных, поддержка многоадресной факсимильной связи и электронной почты, управление многопользовательскими терминалами (принтеры, плоттеры) и др. Файл-сервер (File ...
... 1.5 Уровни помех и линейных затуханий 1.5.1 Электрические помехи в каналах ВЧ связи по ВЛ Электрические помехи имеются в любом канале связи. Они являются основным фактором, ограничивающим дальность передачи информации из-за того, что сигналы, принимаемые приемником, искажаются помехами. Для того чтобы искажения не выходили за пределы, допустимые для данного вида информации, должно быть ...



0 комментариев