Навигация
Устойчивость дискретных систем управления
Реферат
Предмет: Теория автоматического управления
Тема: Устойчивость дискретных систем управления
1. Основные понятия устойчивости дискретных систем
Основные определения устойчивости непрерывных систем справедливы и для дискретных систем с учетом некоторых особенностей.
Необходимым и достаточным условием устойчивости непрерывной линейной системы является расположение в левой полуплоскости всех корней ее характеристического уравнения. Сопоставим, как выглядят уравнения для непрерывных и для дискретных систем.
Для непрерывных систем передаточные функции представляют отношение дробно – рациональных функций и имеют вид
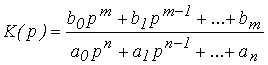 . (1)
. (1)
Характеристическое уравнение ![]() представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома - n .
представляет собой степенное уравнение, при этом число корней уравнения равно степени полинома - n .
Например, для передаточной функции
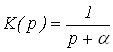
![]()
Для дискретных систем передаточные функции имеют вид
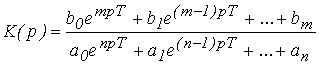 .(2)
.(2)
Характеристическое уравнение ![]() представляет собой трансцендентное уравнение, при этом число корней уравнения бесконечно, так как они имеют периодический характер.
представляет собой трансцендентное уравнение, при этом число корней уравнения бесконечно, так как они имеют периодический характер.
Например, для передаточной функции
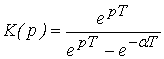 (3)
(3)
корни определяются из соотношений
![]() .
.
Каждому из n корней в плоскости Р, соответствует бесконечное множество периодических корней в плоскости Р*, отстоящих друг от друга на расстоянии частоты квантования и расположенных по группам в каждой полосе. Для анализа свойств системы достаточно анализировать расположение корней в одной, так называемой основной полосе, в качестве которой обычно считают полосу частот ![]() .
.
Расположение корней этого уравнения в комплексной плоскости приведено на рис. 1.
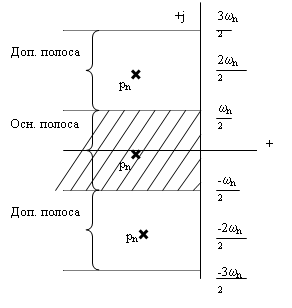
Рис. 1
Дискретная система автоматического управления устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы.
Пример 1. Определить устойчивость дискретной системы с передаточной функцией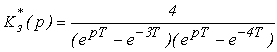 .
.
Решение: Характеристическое уравнение системы имеет вид
![]()
Определим корни характеристического уравнения
![]() .
.
Система устойчива, так как все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы.
Пример 2. Определить устойчивость дискретной системы с передаточной функцией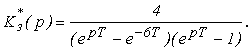
Характеристическое уравнение имеет вид
![]() .
.
Определим корни характеристического уравнения заданной системы
![]() .
.
Система на границе устойчивости, так как один корень расположен на мнимой оси, а второй устойчивый.
2. Определение устойчивости дискретных систем в форме z-преобразования
Использование z-преобразования позволяет преобразовать трансцендентный полином в степенной, что позволяет упростить процесс исследования дискретных систем управления.
Применение z-преобразования (рис. 2.3) отображает основную полосу на плоскость Z, отрезок мнимой оси ![]() в окружность единичного радиуса, а левую часть полосы в круг единичного радиуса.
в окружность единичного радиуса, а левую часть полосы в круг единичного радиуса.
Следовательно, дискретная система устойчива, если все корни ее характеристического уравнения расположены в левой полуплоскости в пределах основной полосы (т. е. условие устойчивости ![]() ).
).
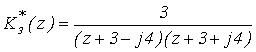 .
.
Характеристическое уравнение имеет вид
![]() .
.
Определим корни характеристического уравнения
![]()
Определим модуль корней
![]() .
.
Система не устойчива, так как модуль корней ее характеристического уравнения меньше единицы.
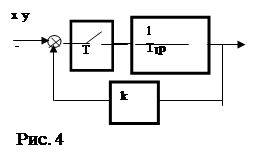
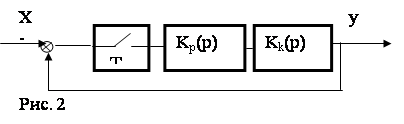
Пример 4. Определить устойчивость дискретной системы, структурная схема которой представлена на рис. 2. 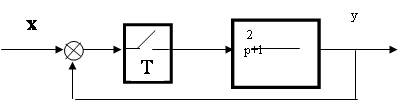
-
![]() Рис. 2
Рис. 2
Решение: Передаточная функция разомкнутой дискретной системы
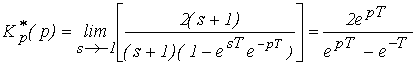 .
.
Передаточная функция разомкнутой дискретной системы в форме z- преобразования
![]() , где
, где ![]()
![]() .
.
Передаточная функция замкнутой дискретной системы в форме z- преобразования
Характеристическое уравнение имеет вид ![]() .
.
Определим корни характеристического уравнения
![]()
При этом модуль корня ![]() при любых допустимых T, следовательно, система устойчива.
при любых допустимых T, следовательно, система устойчива.
Похожие работы
... Определим R(z) , где d=T1 /(T1 +k). 4. Определим величину интеграла J2 с помощью вычетов z1 = d 5. Определим величину интеграла J2 с помощью таблиц 4. Точность дискретных систем управления Точность дискретных САУ оценивается аналогично, как и непрерывных, с учетом некоторых особенностей. Изображение ошибки для дискретной системы равно (5) Установившееся значение ...
... Недостаток: сложность реализации структуры. 2. Реализация дискретных передаточных функций Необходимость реализации дискретных передаточных функций может возникнуть при коррекции дискретных систем управления, при этом используются различные методы. Наиболее часто используют следующие методы: с помощью линий задержки; с помощью импульсных RC-цепей; с помощью методов цифрового моделирования ( ...
... файлов GB_prog.m и GB_mod.mdl, а анализ спектрального состава периодического режима на выходе линейной части – при помощи файлов GB_prog.m и R_Fourie.mdl. Cодержание файла GB_prog.m: %Исследование нелинейных систем методом гармонического баланса %Используемые файлы: GB_prog.m, GB_mod.mdl и R_Fourie.mdl. %Используемые обозначениЯ: НЭ – нелинейный элемент, ЛЧ – линейнаЯ часть. %Очистка всех ...
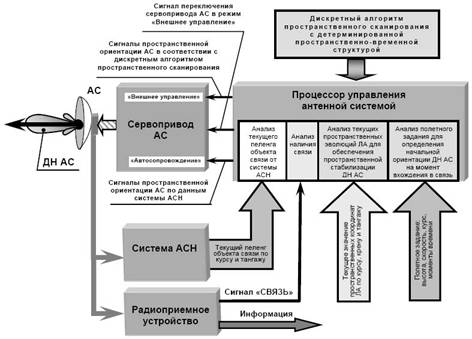
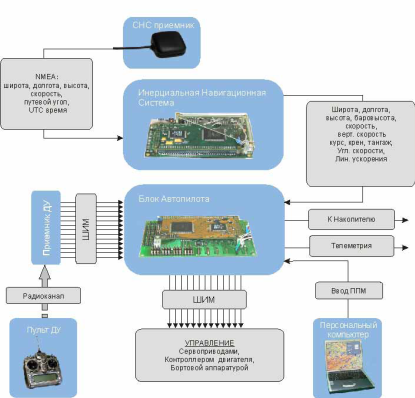
... бортовыми средствами БЛА, на пункт управления. Бортовой комплекс навигации и управления БЛА Бортовой комплекс "Аист" является полнофункциональным средством навигации и управления беспилотного летательного аппарата (БЛА) самолетной схемы. Комплекс обеспечивает: определение навигационных параметров, углов ориентации и параметров движения БЛА (угловых скоростей и ускорений); навигацию и ...
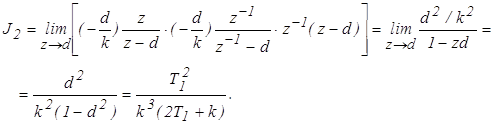

0 комментариев