Навигация
Основные положения синтеза электрических цепей
Академия
Кафедра Физики
Реферат
«Основные положения синтеза электрических цепей»
Орёл 2009
Содержание
Введение………………………………………………………………………..3
Понятие о синтезе электрических цепей……………………………………..4
Условия физической реализуемости передаточных функций……………...4
Этапы решения задачи синтеза ЭЦ…………………………………………...7
Методы аппроксимации заданных характеристик…………………………..9
Литература…………………………………………………………………….16
Введение
Важнейшей составной частью проектирования систем передачи и обработки информации, а также их компонентов, является задача синтеза, под которым понимают построение цепей с заданными свойствами.
Главное в задачах синтеза, непременно подлежащее исполнению, состоит в том, что проектируемая цепь должна воспроизводить с необходимой точностью одну или несколько заданных характеристик.
Понятие о синтезе электрических цепей
Приближенное описание требуемых свойств с помощью математических уравнений, функций, алгоритмов и т.д. в дальнейшем будем называть математической моделью.
Если по ней можно построить электрическую схему, то такую модель называют удовлетворяющей условиям физической реализуемости (УФР) или осуществимости (УФО).
Отметим также тот факт, что одной и той же математической моделью, удовлетворяющей УФР, могут быть поставлены в точное соответствие не одна, а множество схем.
Очевидно, что формулирования УФР для той или иной математической модели не представляются возможным без знания свойств функций линейных электрических цепей. В задачах анализа и синтеза ЛРТУ чаще других используются физически осуществимые математические модели в виде:
- операторных передаточных функций [Т(p),Z(p),Y(p)];
- комплексных передаточных функций [T(jω), АЧХ, ФЧХ];
- временных характеристик [h(t), g(t)].
Рассмотрим свойства лишь некоторых из них, которые в наибольшей мере используются в задачах синтеза ТЭЦ.
Условия физической реализуемости передаточных функций
а) Свойства операторных передаточных функций.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей :
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточных функций располагаются в левой полуплоскости комплексной переменной ![]() . На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции
. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции 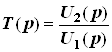 . Выберем входное воздействие
. Выберем входное воздействие ![]() или в операторной форме
или в операторной форме ![]() . Изображение выходного напряжения
. Изображение выходного напряжения ![]() в этом случае численно равно
в этом случае численно равно ![]() , т.е.
, т.е.
 ,
,
где W(p)-полином числителя передаточной функции; А1, А2,… Аm-коэффициенты разложения дробно-рациональной функции на сумму простых дробей. Перейдем от изображения к оригиналу ![]() :
:
![]() (1)
(1)
где в общем случае ![]() .
.
В пассивных и устойчивых активных четырёхполюсниках колебания на выходе четырёхполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что вещественные части полюсов ![]() должны быть отрицательными, т.е. полюсы должны находиться в левой полуплоскости переменной p.
должны быть отрицательными, т.е. полюсы должны находиться в левой полуплоскости переменной p.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей , т.е. ![]() . Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимало бы бесконечно большое значение (т.к. числитель рос бы с увеличением частоты быстрее знаменателя), т.е. цепь обладала бесконечным усилением, что противоречит физическому смыслу.
. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимало бы бесконечно большое значение (т.к. числитель рос бы с увеличением частоты быстрее знаменателя), т.е. цепь обладала бесконечным усилением, что противоречит физическому смыслу.
Итак, будем считать, что ОПФ соответствует УФР, если Т(р) имеет:
- дробно-рациональную математическую конструкцию (![]() );
);
- вещественные коэффициенты ;
- полином знаменателя – полином Гурвица V(p).
б) свойства комплексных передаточных функций.
Из формулы (1) при Р=jω получаем
где ![]() – чётные части полинома, есть функции вещественные;
– чётные части полинома, есть функции вещественные;
![]() – нечётные части полинома являются функциями мнимыми.
– нечётные части полинома являются функциями мнимыми.
Из полученного выражения находим
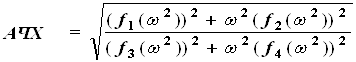 ;
;
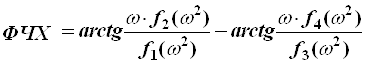 ;
;
Таким образом, АЧХ является иррациональной четной функцией частоты ω,а ФЧХ – нечётной, трансцендентной функцией.
Для математического моделирования более удобной является функция
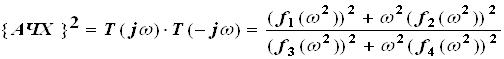
поскольку она во всех случаях есть чётная дробно-рациональная функция.
Её свойства вытекают непосредственно из свойств КПФ и АЧХ и позволяют в простом виде выразить УФР соответствующих математических моделей. Итак, для {АЧХ}2 эти условия имеют следующий вид:
- дробно-рациональные математические конструкции;
- вещественность коэффициентов;
- чётность функций числителя и знаменателя;
- {АЧХ}2![]() 0 для всех ω Є(0,
0 для всех ω Є(0,![]() ).
).
Свойства временных характеристик реальных цепей предлагается изучить самостоятельно.
Этапы решения задачи синтеза ЭЦ
Суть задачи синтеза в наиболее общем виде заключается в отыскании цепи, обладающей требуемыми характеристиками или свойствами и имеющей в своём составе элементы только заранее определенных разновидностей, которые в дальнейшем будем именовать элементным базисом.
Предположим, простоты ради, что синтезируемая цепь должна воспроизводить только одну характеристику ξ (х), под которой может подразумеваться АЧХ, характеристика затухания, временные характеристики и т.д.
В качестве аргумента с «х» чаще всего выступают частота или время.
Как правило ξ (х) задаётся либо в виде графика, либо таблицы и, несколько реже ξ в виде аналитического выражения.
Требуемая функция f (х) всегда задаётся в некотором интервале х Є(ха, хb), который принято называть рабочим интервалом.
Проектируемая цепь на этом интервале в идеальном случае должна иметь соответствующую функцию f (х) точно совпадающей с ξ (х).
Однако этого добиться практически невозможно, да и нет в этом необходимости. Важно, чтобы цепью конечной сложности обеспечивалась необходимая точность совпадений функций f (х) и ξ (х).
Математическое расстояние ρ{ξ(x),f(x)} как характеристика близости функций конструируется таким образом, чтобы это было одно единственное положительное число. В теории синтеза ЭЦ обычно используется Чебышевская оценка точности совпадения функций ξ (х) и f (х). (ЧОТС)
При этом математическое расстояние между ξ (х) и f (х) определяется следующим выражением
![]()
Геометрический смысл чебышевской оценки точности иллюстрируется графиками (рисунок 1).
В общем случае, при синтезе (проектировании) электрических цепей можно выделить два существенных этапа, которые будут рассмотрены в дальнейшем:
1. Нахождение такой f (х), удовлетворяющей УФР, чтобы в рабочем интервале ![]() , где
, где ![]() - заданная точность воспроизведения. Назовём это этапом аппроксимации.
- заданная точность воспроизведения. Назовём это этапом аппроксимации.
Похожие работы
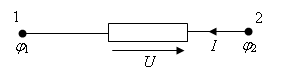
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
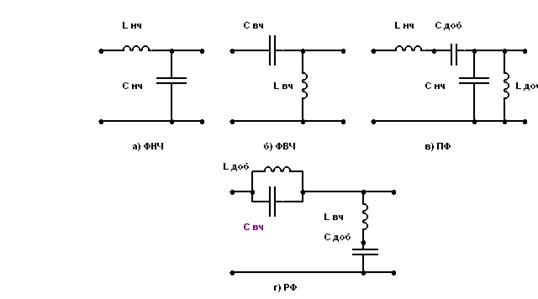
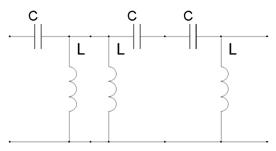
... курсовой работе, в соответствии с заданием, необходимо решить следующие задачи: - разработать (любым методом) эквивалентную, принципиальную схемы электрического фильтра на любых радиокомпонентах; - разработать усилитель напряжения на любых радиоэлементах (схему электрическую принципиальную); - любым методом рассчитать спектр сложного периодического сигнала, подаваемого с “генератора импульсов” ...
... метода применимы только для линейных электрических цепей, поскольку в их основе лежит метод наложения (суперпозиции). Сущность классического метода анализа переходных колебаний в электрических цепях Переходные процессы в электрических цепях описываются уравнениями, составленными на основании законов Кирхгофа для мгновенных значений напряжений и токов. Эти уравнения для различных цепей после ...
... сопротивление) механически из схемы не исключается. Отметим, что ступенчатое воздействие является простейшей функцией. Нахождение реакции на такое воздействие является одной из важных задач в теории переходных процессов (аналогично задаче нахождения реакции цепи на гармоническое воздействие в стационарном режиме). в) другие воздействия, например, в виде импульсов различной формы, включение и ...





0 комментариев