Навигация
1 кгс або 1кГ ; кГ = 9.8 Н.
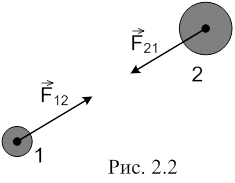 Будь-яка дія тiл одного на друге носить характер взаємодії: якщо тіло 1 діє на тіло 2 з силою
Будь-яка дія тiл одного на друге носить характер взаємодії: якщо тіло 1 діє на тіло 2 з силою ![]() , то i тіло 2 в свою чергу діє на тіло 1 з силою
, то i тіло 2 в свою чергу діє на тіло 1 з силою ![]() (рис. 2.2).
(рис. 2.2).
Третій закон Ньютона стверджує, що сили, з якими тiла діють одне на одне, рiвнi за значенням i протилежні за напрямом:
4. ЗАКОН ЗБЕРЕЖЕННЯ ІМПУЛЬСУ
Перетворимо (2.1) наступним чином:
![]()
![]() або
або ![]() (2.11)
(2.11)
Назвемо імпульсом системи м.т. векторну суму iмпульсiв окремих м.т. системи: ![]() Одержимо:
Одержимо:
![]() (2.11')
(2.11')
Нагадаємо, що (2.1) було записано для ізольованої системи двох матеріальних точок.
Отже, повний імпульс ізольованої системи двох м.т. залишається сталим.
Це твердження (i рівняння (2.11) чи (2.11')) називають законом збереження імпульсу для ізольованої системи двох м.т.
Розглянемо тепер систему, що складається з N м.т. Для кожної м.т. запишемо рівняння руху (2.5):
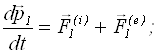
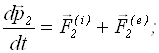
![]()
де ![]() - внутрiшнi сили, -
- внутрiшнi сили, -![]() зовнiшнi сили. Додамо ці рівняння, враховуючи, що внутрiшнi сили згідно третього закону Ньютона зустрічаються попарно i їх векторна сума дорівнює нулю:
зовнiшнi сили. Додамо ці рівняння, враховуючи, що внутрiшнi сили згідно третього закону Ньютона зустрічаються попарно i їх векторна сума дорівнює нулю:
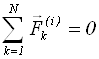 ;
;
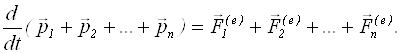
В дужках стоїть імпульс системи м.т., тому:
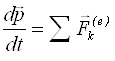 (2.12)
(2.12)
(2.12) - це другий закон Ньютона для системи м.т.
Для замкнутої системи ![]() тому
тому 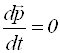 і
і ![]()
Імпульс ізольованої системи м.т. зберігається, тобто залишається сталим в часі.
Імпульс зберігається i для незамкнутої системи, якщо 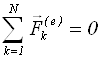 .
.
Якщо сума зовнiшнiх сил не дорівнює нулю, але проекція цієї суми на деякий напрямок рівна нулю, то зберігається складова імпульсу в цьому напрямку (тобто проекція імпульсу на цей напрямок):
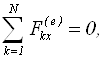
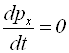 і
і ![]()
Імпульс системи м.т. може бути представлений у вигляді добутку сумарної маси системи м.т. на швидкість руху центра мас системи:
![]() (2.13)
(2.13)
Центром мас системи називають таку точку C, положення якої задається радiус-вектором ![]() :
:
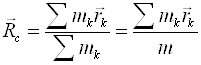 (2.14)
(2.14)
Для твердого тіла: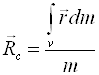 .
.
Продиференцiюємо (2.14) за часом i одержимо (2.13):
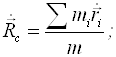
![]()
![]()
Підставимо (2.13) в (2.12) :
 , або
, або ![]() (2.15)
(2.15)
Центр мас системи м.т. рухається як матеріальна точка, маса якої дорівнює сумарній масі всієї системи, i на яку діє сила, що дорівнює геометричній сумі всіх зовнiшнiх сил, що діють на систему.
Це твердження називають теоремою про рух центра мас.
Для ізольованої системи : ![]()
![]()
Центр мас ізольованої системи або нерухомий, або рухається рiвномiрно i прямолiнiйно.
Якщо початок вiдлiку помістити в центр мас (система вiдлiку залишиться iнерцiальною, оскільки ![]() ), то
), то ![]() ,
, ![]() і
і ![]()
Центр мас є точка простору, відносно якої повний імпульс ізольованої системи дорівнює нулю.
5. РЕАКТИВНИЙ РУХ.
Розглянемо рух тiла зі змінною масою. Мається на увазі не релятивістська залежність маси тiла вiд швидкості, оскільки мова йтиме про відносно повільний рух тiл, а зміна маси тiла за рахунок втрати чи поповнення ним речовини.
Один з прикладів такого руху - рух ракети. Ракета з великою швидкістю викидає речовину (гази), діючи на неї з великою силою. Речовина, що викидається, з такою ж, але протилежно направленою силою в свою чергу діє на ракету i надає їй прискорення в протилежному напрямі. Якщо зовнiшнiх сил немає, то імпульс системи "ракета - викинута речовина" не змінюється з часом.
Розглянемо загальний випадок, коли на ракету діють зовнiшнi сили. Нехай m(t) - маса ракети в довільний момент часу t , а ![]() - її швидкість. Імпульс ракети в цей момент часу дорівнює
- її швидкість. Імпульс ракети в цей момент часу дорівнює ![]() . Через час dt маса i швидкість одержать прирости
. Через час dt маса i швидкість одержать прирости ![]()
![]() i
i ![]() . Імпульс ракети тепер дорівнює
. Імпульс ракети тепер дорівнює ![]() . Імпульс газів, що утворилися за цей же час dt, дорівнює dmгаз
. Імпульс газів, що утворилися за цей же час dt, дорівнює dmгаз![]() газ , де dmгаз - маса газів,
газ , де dmгаз - маса газів, ![]() газ - їх швидкість. Приріст імпульсу ракети дорівнює імпульсу рiвнодiйної зовнiшнiх сил (див. (2.12)):
газ - їх швидкість. Приріст імпульсу ракети дорівнює імпульсу рiвнодiйної зовнiшнiх сил (див. (2.12)):
(m + dm)(![]() + d
+ d![]() ) + dmгаз
) + dmгаз![]() газ - m
газ - m![]() =
= ![]() dt.
dt.
Розкриємо дужки:
m![]() + md
+ md![]() +
+ ![]() dm + dm·d
dm + dm·d![]() + dmгаз
+ dmгаз![]() газ - m
газ - m![]() =
= ![]() dt
dt
Оскільки dt - мала величина ( dt ![]() 0 ), то dm·d
0 ), то dm·d![]() - нескінченно мала величина вищого порядку i її можна відкинути; dmгаз = - dm згідно закону збереження маси. Після перетворень одержимо:
- нескінченно мала величина вищого порядку i її можна відкинути; dmгаз = - dm згідно закону збереження маси. Після перетворень одержимо:
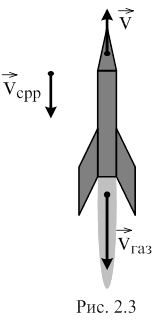 md
md![]() - dm(
- dm(![]() газ -
газ -![]() ) =
) =![]() dt
dt
Різниця ![]() газ -
газ -![]() =
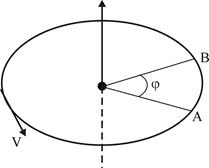
= ![]() відн - це швидкість витікання газів відносно ракети; її називають швидкістю газової струмини (див.рис.2.3).
відн - це швидкість витікання газів відносно ракети; її називають швидкістю газової струмини (див.рис.2.3).
(Якщо ракету взяти за нерухому СВ то слід вважати що оточуюче середовище рухається зі швидкістю ![]()
![]() відн
відн![]() газ
газ![]() срр;
срр; ![]() відн
відн![]() газ
газ![]() ).
).
Отже:
![]() =
=![]() dt+
dt+![]() (2.16)
(2.16)
Розділимо (2.16) на dt :
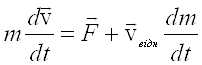 (2.17)
(2.17)
За формою (2.17) співпадає з рівнянням другого закону Ньютона. Однак маса тут не постійна, а змінюється з часом. До зовнішньої сили ![]() додається член
додається член 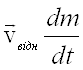 , який носить назву реактивної сили:
, який носить назву реактивної сили:
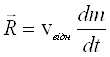 (2.18)
(2.18)
Якщо маса вiддiляється, то ![]() < 0 i вектор
< 0 i вектор ![]() протилежний вектору
протилежний вектору ![]() відн ; якщо маса приєднується, то
відн ; якщо маса приєднується, то ![]() > 0 i вектор
> 0 i вектор ![]() співпадає за напрямком з
співпадає за напрямком з ![]() відн .
відн .
Рівняння (2.17) i еквівалентне йому рівняння (2.16) називають рівнянням руху точки iз змінною масою або рівнянням Мещерського (Мещерський I.В. (1859 - 1935)).
Якщо ![]() = 0, то з (2.16) одержимо:
= 0, то з (2.16) одержимо:
![]()
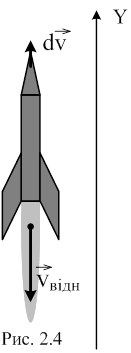
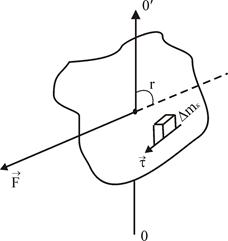
Нехай ракета рухається в напрямку, протилежному ![]() . Спроектуємо останню рiвнiсть на вісь OY (див. рис. 2.4):
. Спроектуємо останню рiвнiсть на вісь OY (див. рис. 2.4):
mdv = - vвідн dm;
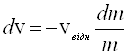 (2.19)
(2.19)
Будемо вважати, що vвідн стала; тодi розв`язування рівняння (2.19) спрощується:
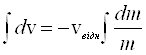
![]() (2.20)
(2.20)
Значення C визначимо з початкових умов (якщо
v0 = 0, то початкова маса дорівнює m0), якi пiдставимо в (2.20):
![]() ,
звiдки
,
звiдки ![]() .
.
Таким чином: ![]()
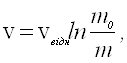
або 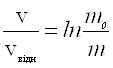 .
Остаточно:
.
Остаточно:
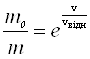 (2.21)
(2.21)
(2.21) називають формулою Ціолковського (К.Е. Цiолковський (1857-1935)).
(Застосування (2.21) до польотів космічних ракет дає наступні значення відношень![]() . При vвідн=1 км/c для v1=8 км/c матимемо
. При vвідн=1 км/c для v1=8 км/c матимемо 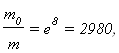 що нереально (потрібні кращі сорти палива). При vвідн=4 км/c
що нереально (потрібні кращі сорти палива). При vвідн=4 км/c 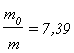 (політ в одну сторону)).
(політ в одну сторону)).
6. ПРИНЦИП ВІДНОСНОСТІ ГАЛІЛЕЯ.
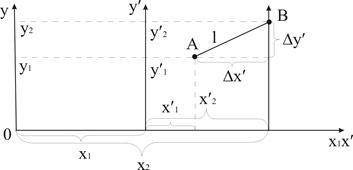
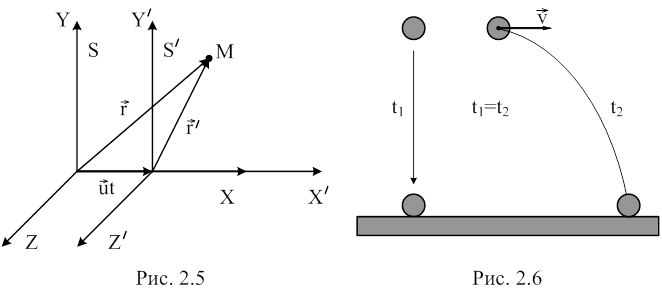 Розглянемо дві iнерцiальнi системи вiдлiку -
Розглянемо дві iнерцiальнi системи вiдлiку - ![]() i
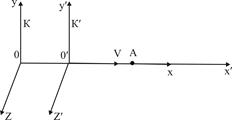
i ![]() (див. рис. 2.5). Нехай S - нерухома СВ, а S' - рухається відносно S зі сталою швидкістю
(див. рис. 2.5). Нехай S - нерухома СВ, а S' - рухається відносно S зі сталою швидкістю ![]() . Для простоти вважатимемо, що
. Для простоти вважатимемо, що ![]() направлена вздовж вiсi OX i в момент часу t0 = 0 осi координат систем
направлена вздовж вiсi OX i в момент часу t0 = 0 осi координат систем ![]() i
i ![]() співпадали. Нехай в момент часу t рухома точка знаходиться в положенні M.
співпадали. Нехай в момент часу t рухома точка знаходиться в положенні M.
Тоді: ![]() .
.
Припустивши, що час в обох СВ однаковий (абсолютнiсть часу), тобто t=t´, одержимо:
![]() , (2.22)
, (2.22)
або в координатній формі:
 (2.23)
(2.23)
(2.22) та (2.23) називають перетвореннями Галілея. Крім припущення про абсолютність часу тут використано також припущення про абсолютність довжин: в рiвняннi ![]()
![]() і
і ![]() вимірюються в різних СВ S i S´. Ці припущення справедливі лише при u << c. При u ≈ c перетворення Галілея повинні бути замiненi більш загальними перетвореннями Лоренца, якi будуть розглянуть пiзнiше.
вимірюються в різних СВ S i S´. Ці припущення справедливі лише при u << c. При u ≈ c перетворення Галілея повинні бути замiненi більш загальними перетвореннями Лоренца, якi будуть розглянуть пiзнiше.
Візьмемо похідну вiд (2.22) по часу:
![]() (2.24)
(2.24)
(2.24) - це класичний закон додавання швидкостей :
![]()
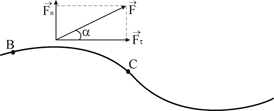
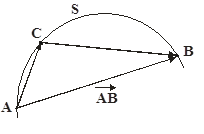
Під час розв`язування задач доводиться розглядати рух тiл відносно різних СВ. При цьому ми будемо користуватися принципом незалежності рухiв, згiдно якому рухи даного тiла відносно різних СВ не залежать один вiд одного. Як приклад можна навести рух тiл, одне з яких кинуто горизонтально, а друге вільно падає без початкової швидкості (див. рис. 2.6).
Візьмемо похідну вiд (2.24) по часу (врахуємо, що ![]() ):
):
![]()
тобто: ![]() (2.25)
(2.25)
Отже, прискорення якого-небудь тiла в усіх СВ, які рухаються одна відносно іншої прямолiнiйно i рiвномiрно, одне й те ж. Тому якщо одна із систем iнерцiальна, то й iншi також будуть IСВ. Про рiвнiсть (2.25) говорять, що прискорення iнварiантне відносно перетворень Галілея. Можна показати, що сила є функцією тільки iнварiантних величин - рiзницi координат i рiзницi швидкостей точок, що взаємодіють одна з одною. З цієї причини сила також iнварiантна відносно перетворень Галілея.
Тому рівняння другого закону Ньютона в ІСВ S´ має такий же вид, як i в S:
![]()
Рівняння механіки Ньютона iнварiантнi відносно перетворень Галілея.
Це твердження називається принципом вiдносностi Галілея.
Іншими словами він звучить так:
всі механiчнi явища в різних IСВ відбуваються однаково, внаслiдок чого ніякими механічними дослідами неможливо встановити, чи нерухома дана СВ, чи вона рухається рiвномiрно i прямолiнiйно.
Похожие работы
... ї енергії обертального руху твердого тіла. Пояснити, що в обертальному русі твердого тіла мірою його інертних властивостей є момент інерції. Визначити рівняння динаміки обертального руху, пояснити за допомогою "Лектора-2000" та сформулювати закон збереження імпульсу. Гіроскопічний ефект пояснити за допомогою гіроскопу та "Лектора-2000". Звернути увагу на його застосування. Вступ При порі ...
... математики. Фізика є теоретичним фундаментом для вивчення професійно-орієнтованих, військово-технічних і військових дисциплін. Тема 1. Кінематика і динаміка матеріальної точки Навчальний потік інженери Час 2 години Місце Навчальна та виховна мета _________________________________________ ____________________________________________________________ Навчальні питання і розподіл часу ...
... осаду РbCl2 при дії на розчини солей свинцю (ІІ) соляною кислотою або розчинними хлоридами; г) утворення жовтого осаду РbCl2 при введенні йодид-іонів в розчини солей свинцю (ІІ). 6. Основні закони хімії та їх наслідки 1. Закон збереження маси речовини: маса речовин, які вступили в реакцію, дорівнює масі речовин, отриманих внаслідок реакції. 2. Закон сталості складу: кожна чиста речовина ...
... сники (майстри і підмайстри) і купці. Формами права були збірники звичаєвого права (“Руська правда”), “Мірило праведне”, “Корчма”, Номоканон, князівські привілеї (грамоти) тощо. Державний устрій Руси-України Початковий етап розвитку Русі в державно-організаційному аспекті мало чим відрізнявся від організаційних рис, які були властиві княжінням. Об’єднавчі процеси вносили зміни і в організац ...

0 комментариев