Навигация
4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Целесообразно, для круглого отверстия, использовать полярные координаты вместо прямоугольных. Пусть ![]() – полярные координаты произвольной точки отверстия:
– полярные координаты произвольной точки отверстия:
![]()
![]() (4.1)
(4.1)
(ω, ψ) – координаты точки P в дифракционной картине, относящейся к геометрическому изображению источника, т.е.
![]()
![]() (4.2)
(4.2)
Из определения полярных координат следует: ω = ![]()
Запишем интеграл, описывающий дифракцию Фраунгофера (полное возмущение в точке P), в виде
![]() (4.3)
(4.3)
здесь C – величина, определяющаяся через величины связанные с положениями источника и точки наблюдения, однако, на практике она удобнее выражается через другие величины.
 (4.4)
(4.4)
λ – длина световой волны;
E – полная энергия, падающая на отверстие;
D – площадь отверстия ![]() ;
;
a – радиус отверстия;
k – волновое число 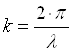 .
.
Т.к. интенсивность выражается формулой:
![]() (4.5)
(4.5)
интенсивность в центре картины (p = 0,q = 0) равна
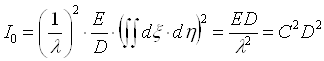 (4.6)
(4.6)
5. РЕШЕНИЕ, АНАЛИЗ РЕЗУЛЬТАТОВ
Решение поставленной задачи произведем по методу, изложенному в [1].
Если a принять за радиус круглого отверстия, то дифракционный интеграл (4.3) примет вид
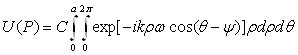 (5.1)
(5.1)
Теперь используя интегральное представление функций Бесселя (5.2)
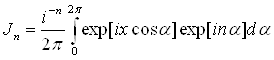 (5.2)
(5.2)
сведем уравнение (5.1) к
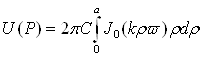 (5.3)
(5.3)
используя рекуррентное свойство бесселевых функций (5.4)
![]() (5.4)
(5.4)
дающее после интегрирования для n = 0
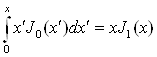 (5.5)
(5.5)
из (5.3) и (5.5) следует, что
![]() (5.6)
(5.6)
,где D = p·a2. Следовательно, интенсивность определяется выражением
![]() (5.7)
(5.7)
,где I0 = C2D2 = ED/λ2 – в соответствии с (4.6)
Распределение интенсивности в окрестности геометрического изображения описывается функцией 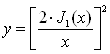 , график которой приведен в приложении 1.
, график которой приведен в приложении 1.
Она имеет главный максимум y = 1 при x = 0 и с увеличением x осциллирует с постепенным уменьшением амплитуды подобно функции 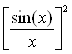 распределения интенсивности при дифракции на прямоугольном отверстии.
распределения интенсивности при дифракции на прямоугольном отверстии.
Интенсивность равна нулю (минимум) при значениях x, определяемых J1(x) = 0. Положения вторичных максимумов определяются значениями x, удовлетворяющими уравнению 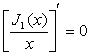 , или, используя формулу (5.4) – корнями уравнения J2(x) = 0.
, или, используя формулу (5.4) – корнями уравнения J2(x) = 0.
Минимумы и максимумы не строго эквидистантны, при увеличении x, расстояния между последовательными максимумами или минимумами приближаются к p (см. рис.2. приложения 1)
Корни уравнения J1(x) = J2(x) = 0 для нахождения минимумов и максимумов функции приведены в табл.5.1.
| J1(x) = 0 {y(x) = 0} | J2(x) = 0 | y(x) |
| 3.83171 | 0 | 1 |
| 7.01559 | 5.13564 | 0.0175 |
| 10.17347 | 8.41722 | 4.158E-3 |
| 13.32369 | 11.61993 | 1.60064E-3 |
| 16.47063 | 14.79609 | 7.79445E-4 |
| 19.61586 | 17.95982 | 4.37026E-4 |
| 22.76008 | 21.11698 | 2.69287E-4 |
Таблица 5.1 - Корни уравнения J1(x) = J2(x) = 0
На рис.3. приложения представлено семейство характеристик, описывающих конкретный случай, при a – const (a = 0.1·10-3 м) и различных длинах волн λ (400 нм, 500 нм, 600 нм). Из графика видно, что угловой радиус ω прямо пропорционален длине волны падающего света.
На рис.4. приложения представлено семейство характеристик, описывающих конкретный случай, при λ – const (λ = 600·10-9 м) и различных радиусах отверстий a (1·10-4 м, 2·10-4 м, 3·10-4 м). Из графика видно, что угловой радиус ω обратно пропорционален радиусу отверстия. При увеличении радиуса отверстия характеристика принимает более резкий характер.
6. ВЫВОДЫ
В данном курсовом проекте была изучена функция распределения интенсивности света 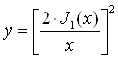 при дифракции от круглого отверстия и что она в действительности зависит от длины волны падающего пучка света, а также от радиуса отверстия. Можно также заметить, что интенсивность светового пучка резко падает по отношению к первому максимуму I0 и соотносится между собой как 1000 : 17.5 : 4.2 : 1.6 : 0.8.
при дифракции от круглого отверстия и что она в действительности зависит от длины волны падающего пучка света, а также от радиуса отверстия. Можно также заметить, что интенсивность светового пучка резко падает по отношению к первому максимуму I0 и соотносится между собой как 1000 : 17.5 : 4.2 : 1.6 : 0.8.
Найденные результаты показывают, что наблюдаемая картина имеет вид светлого диска с центром в геометрическом изображении источника (p = 0, q = 0), окруженного светлыми и темными кольцами. Интенсивность светлых колец быстро уменьшается с увеличением радиуса и обычно только одно или два первых кольца достаточно ярки, чтобы их можно было наблюдать невооруженным глазом.
7. ЗАКЛЮЧЕНИЕ
Поставленная задача была решена, используя классические методы расчета, основанные на хорошо зарекомендовавших себя функциях Бесселя.
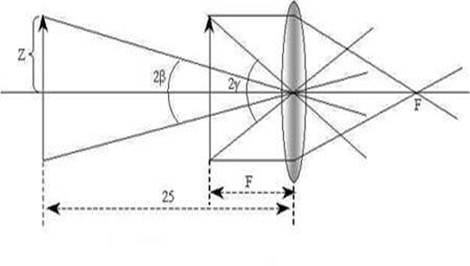
Случай дифракции параллельных световых волн на круглом отверстии имеет большое практическое значение, поскольку все оправы линз и объективов имеют обычно круглую форму, так что при расчете любого оптического инструмента приходится принимать в расчет дифракцию света на оправах линз.
СПИСОК ЛИТЕРАТУРЫ
1. Борн М., Вольф Э. Основы оптики. –М.: Наука, 1970. – 856 с.
2. Ландсберг Г.С. Оптика. –М.: Наука, 1976. – 928 с.
3. Орловская Л.В. Изучение дифракции лазерного излучения от круглого отверстия. –Томск, 1985. – 10 с. (Ротапринт ТИАСУРа).
ПРИЛОЖЕНИЕ 1
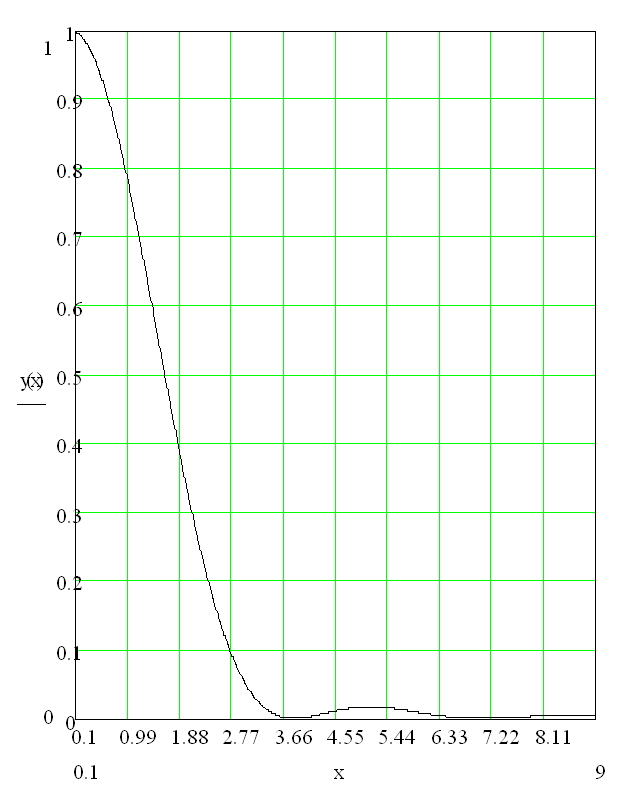
Уменьшенный график функции ![]()
Рис.1. Дифракция Фраунгофера на круглом отверстии.
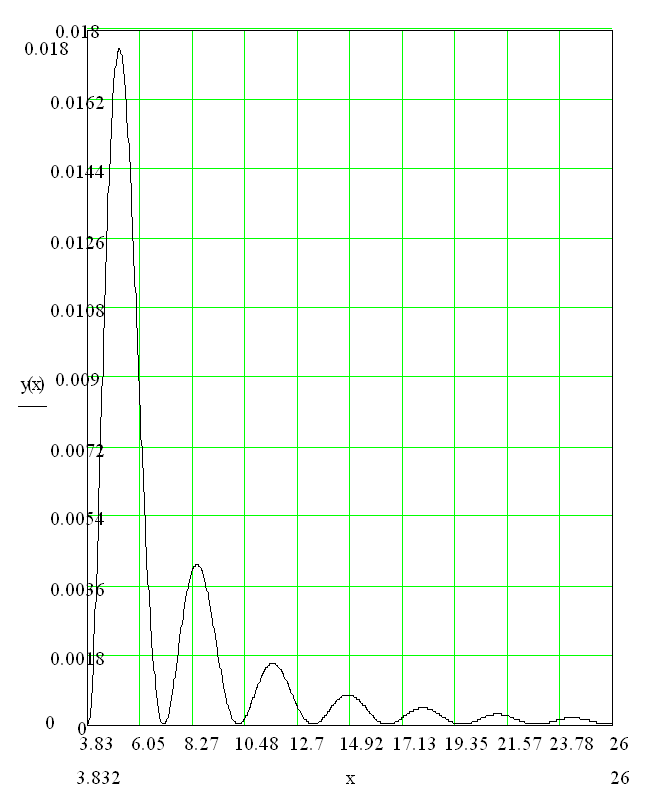
Рис.2 Увеличенный график функции ![]() , начинающийся с первого минимума.
, начинающийся с первого минимума.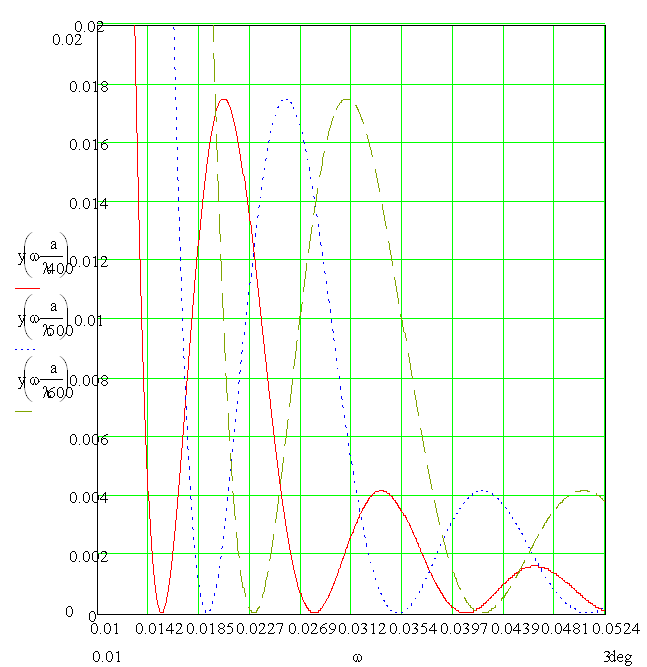
Рис.3. Семейство характеристик при различных длинах волн.
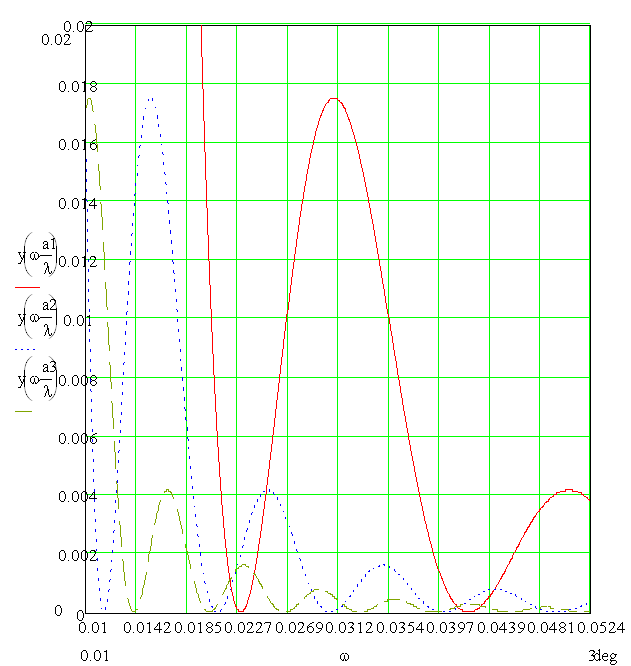
Рис.4 Семейство характеристик при различных радиусах отверстий.
Похожие работы
... применяют линзы и зеркала со сферическими поверхностями, но для упрощения оптических систем и повышения качества изображений при высокой светосиле используют оптические элементы. Глава 1. Оптические инструменты, вооружающие глаз. 1.1. Оптические приборы для визуальных наблюдений Для невооруженного глаза наименьший угол зрения приблизительно равен 1'. Этот угол определяется мозаичным строением ...
... , той самой дифракции, которая в своё время подтвердила наличие волновых свойств у электронов и ставит в наши дни предел разрешения в электронном микроскопе. В случае электронов объектами, в которых может происходить дифракция на периодической структуре (аналогичной объёмной дифракционной решётке в оптике), служат кристаллические структуры. Известно, что в кристаллах атомы расположены в строгом ...
... им бликов. Луч лазера занимает на компакт-диске настолько малую площадь, что этот участок можно считать одномерной дифракционной решеткой. Схема прибора (прибор №1), для наблюдения дифракции света на кусочке компакт-диска, играющего роль отражательной дифракционной решетки, представлена на рисунке 2. Здесь: 1 – источник света – лазер-брелок, укрепленной на поворачивающейся ...
... Гюйгенса-Френеля. На рис 18_2 приведена фотография распределения интенсивности света, дифрагировавшего на небольшом отверстии прямоугольной формы, и результат расчетов интенсивности по формуле (1). Интерференция. В предельном случае дифракции на экране с бесконечно-малыми отверстиями (математически описываемыми при помощи дельта-функций) говорят об интерференции, наблюдаемой методом деления ...
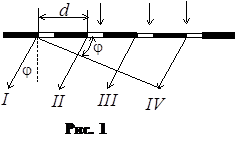

0 комментариев