Навигация
Определяем перемещение свободного конца бруса
4. Определяем перемещение свободного конца бруса
∆l=∆l1+∆l2+∆l3![]()
∆l1=![]() =
=![]() = – 0,5мм
= – 0,5мм
∆l2=![]() =
=![]() = – 0,225мм
= – 0,225мм
∆l3=![]() =
=![]() = 0,05мм
= 0,05мм
∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
Задача № 2
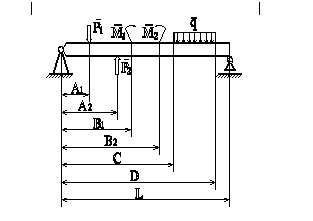
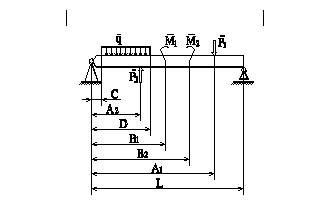
Из условия прочности определить размеры поперечного сечения стержня, удерживающего в равновесии балку, если предел текучести материала σ т=320МПа, заданный коэффициент запаса прочности [n] = 2,5. Расчет провести для двух случаев:
1. поперечное сечение стержня – круг;
2. поперечное сечение стержня – квадрат.
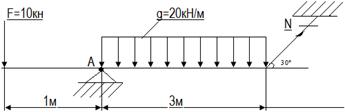
Вторая задача может быть решена студентами, если они будут ясно представлять смысл условия прочности при растяжении (сжатии).
Последовательность решения задачи:
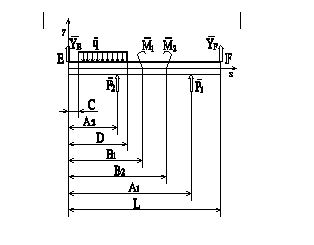
Балку, равновесие которой рассматривается, освободить от связей и заменить действия связей их реакциями;
Составить уравнение равновесия, причем принять за точку, относительно которой определяются моменты, точку в которой установлена опора, и определяем продольную силу N;
Определить из условия прочности площадь поперечного сечения стержня;
Определить для двух случаев размеры поперечного сечения стержня.
Для круга – диаметр d;
Для квадрата – сторону a.
Решение
Составляем уравнение равновесия и определяем продольную силу N
Σ m A=0
N∙sin30°∙3 – 3q∙1,5 + F∙1 = 0
N=![]() =
=![]() = 53,3 кН
= 53,3 кН
2. Определяем допускаемое нормальное напряжение
| [σ]= | σ | = |
| [n] |
3. Определяем площадь поперечного сечения стержня
| σmax | = | N | ≤ [σ]→A ≥ | N | = | 53,3∙103 | =416 мм2 |
| A | [σ] | 128 |
4. Определяем размеры попе речного сечения круга – диаметр d
А=![]() →d=
→d=![]() =
=![]() = 23 мм
= 23 мм
5. Определяем размеры поперечного сечения квадрата – сторону a
A=a2→a=![]() =
=![]() = 20,4 мм.
= 20,4 мм.
IV. Задания для самостоятельного решения
Задача №1
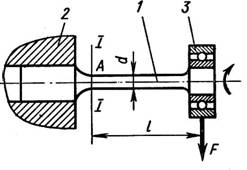
Проверить прочность стальной тяги ВО диаметром d=20мм,если предел текучести σт =240МПа.требуемый коэффициент запаса прочности [n]=1,5
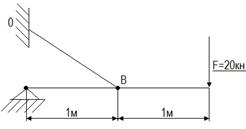
Ответ: перегружена на 58,75%
Задача 2.
Проверить прочность стальных брусьев, если [σ]=160МПа
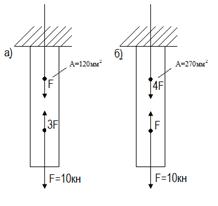
Ответ: а) перегружен на 4,4%
б) недогружен на 7,5%
Задача 3.
Определить требуемую площадь А поперечного сечения стального бруса, если [σ]=160МПа,
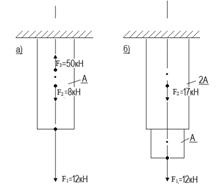
Ответ: а) А=188мм2
б) А=90,6мм2
Задача№4
Определить допускаемую нагрузку для стального стержня, если σт =250МПа, [n]=1,6

Ответ: [F]=31,2кН
Задача №5
Определить размеры поперечного сечения стержня кронштейна, если [σр]=160МПа, [σсж]=120МПа
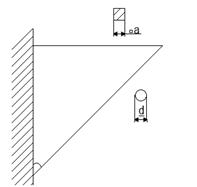
Ответ: а=10мм,d=10мм.
Список литературы
1. Иукович Г.М. «Сопротивление материалов» М. «Высшая школа» 2004г
2. Иукович Г.М. «Сборник задач по сопротивлению материалов» М.«Высшая школа» 2001г.
3. Мовнин М.С. и другие «Руководство к решению задач по технической механике» М. «Высшая школа» 2006г.
Похожие работы
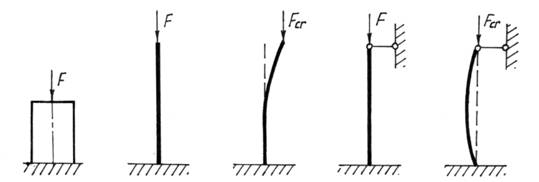
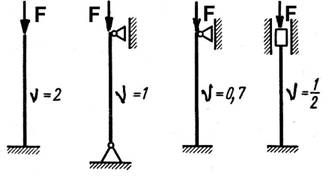
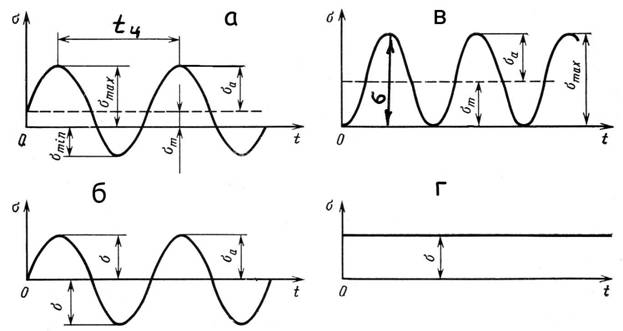
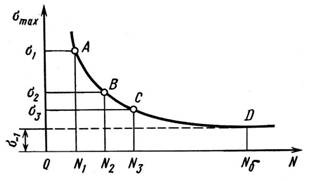
... – на рис. 3, г. Отметим, что применение формулы (5.99) правомерно только при условии, что деформация сжатого стержня в момент потери начальной формы равновесия является упругой. Рис. 3 Прочность при циклически изменяющихся нагрузках (напряжениях). Понятие об усталости материалов Работа механизмов характеризуется определенностью движений и нагружений звеньев, повторяемостью через ...
... Ѕ–207,9Ѕ> 160. комитет по высшему образованию Российской Федерации Московская Государственная Академия Тонкой Химической Технологии им. М.В. Ломоносова кафедра : “Прикладная механика и основы конструирования.” Расчетно-графическая работа № 2 : “Расчет нагруженной балки” Вариант №: 24 студент: Холин Андрей Юрьевич (группа Е-203) преподаватель: Сергеев Александр Иванович 1998г. Задание ...
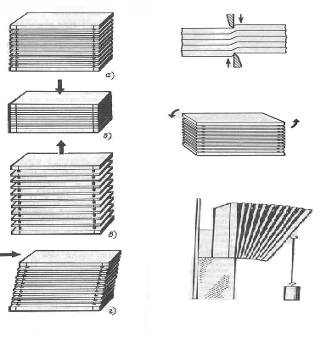
... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...
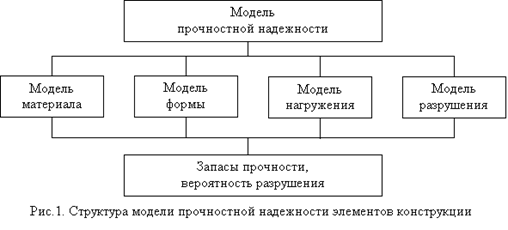
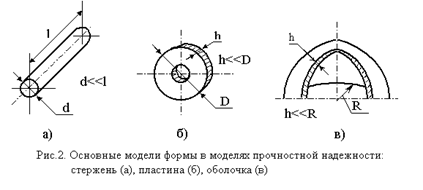
... характере деформирования Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в сопротивлении материалов приходится вводить свою модель — модель идеализированного ...
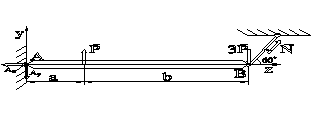
0 комментариев