Навигация
Дисперсійна крива кристала
1.1 Дисперсійна крива кристала
Основні риси частотно-кутового спектру СПР визначаються дисперсійній кривій (k) wкристала. Дисперсійне співвідношення кубічного (неанізотропного) кристала в гармонійному наближенні в одно резонансном випадку має вигляд:
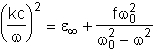 , (2)
, (2)
де e![]() - діелектрична проникність середовища на частотах багато великих фундаментальних частот кристалічної решітки, але багато менших частот електронних переходів, f=0-e
- діелектрична проникність середовища на частотах багато великих фундаментальних частот кристалічної решітки, але багато менших частот електронних переходів, f=0-e![]() - сила осцилятора, w0 - фундаментальна частота оптичного коливання грат. На рис.1 приведена дисперсійна крива відповідна рівнянню (2). Якби поперечні механічні коливання і електромагнітні хвилі були незалежні, то перші описувалися би прямими.
- сила осцилятора, w0 - фундаментальна частота оптичного коливання грат. На рис.1 приведена дисперсійна крива відповідна рівнянню (2). Якби поперечні механічні коливання і електромагнітні хвилі були незалежні, то перші описувалися би прямими.
Мал.1 Дисперсія кубічного кристала
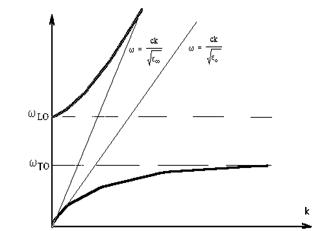
Мал.2 Дисперсія анізотропного кристала
(k)=wTO і (k)=wLO,
а другі - прямій
w=![]() .
.
Взаємодія, що запізнюється, між цими коливаннями в кристалі приводить до поляритонным збуджень, що мають змішану електромеханічну природу. На частотах, великих wLOзнаходитися верхня поляритонная гілка. На частотах між wTOі wLOзнаходиться заборонена зона, де середовище не прозоре для об'ємних хвиль.
У анізотропних одноосних кристалах частотам поперечних і подовжніх коливань wТ і wL відповідають частоти коливань, зсуви яких паралельні (wеТ; еL) і перпендикулярні (оТ; wоL) оптичній осі. На рис.2 зображені дисперсійні криві, відповідні злучаю, коли вектор ![]() перпендикулярний головній оптичній осі кристала.
перпендикулярний головній оптичній осі кристала.
1.2 Інтенсивність СПР і симетрія кристала LiNbO3
Вперше питання про інтенсивність СПР розглядалося в роботі [3]. Коли поляритонна частота p wдалека від частоти фонона, досить розглядати квадратичну нелінійну сприйнятливість (2).c Розглядатимемо накачування, як плоску монохроматичну хвилю з інтенсивністю SL і припустимо, що кути розсіяння p,s qна частотах pw, s wмалі, так що
![]()
де А - перетин розсіюючого об'єму V, l - довжина кристала. Тоді потужність, що розсіюється на частоті ws в напрямі ![]() у одиничний спектральний і кутовий інтервали, рівна[4]:
у одиничний спектральний і кутовий інтервали, рівна[4]:
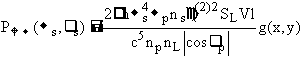 (3)
(3)
де ![]() - згортка тензора (2)c і ортов поляризації відповідних хвиль, ns,p,L - показники заломлення на відповідних частотах, а
- згортка тензора (2)c і ортов поляризації відповідних хвиль, ns,p,L - показники заломлення на відповідних частотах, а
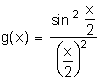 -
-
форм-фактор, що описує частотно-кутову структуру СПР, коли середовище прозоре на всіх трьох частотах. У останньому виразі введено позначення
![]() ,.где
,.где ![]() -
-
настроєння хвилевого вектора поляритону від точного синхронізму.
Тензор квадратичної сприйнятливості (2)c однорідних кристалів ніобіту літію, що використалися в даній роботі, має вигляд [5]:
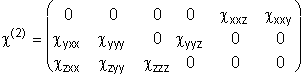 , (4)
, (4)
причому cxxy=-2yyyc, cyxx=-yyy, cyyz=xxz, zyy=zxx. Кристалофізичні осі орієнтовані щодо елементів симетрії таким чином: вісь Z співпадає з оптичною віссю кристала, віссю симетрії третього порядку, вісь X перпендикулярна площині дзеркальної симетрії m, а вісь Y лежить в цій площині. Геометрії розсіяння, яка була реалізована в експерименті, відповідає схематичний запис X(Z,Y) X+Z. DТут послідовність індексів задає напрями векторів ![]() відповідно. Останній вираз X+Z Dвизначає площина розсіяння, яка, у свою чергу, задається орієнтацією вхідної щілини спектрографа (в даному випадку площина XZ). Відповідно до виду тензора нелінійної поляризуемости (4) константа нелінійної взаємодії рівна:
відповідно. Останній вираз X+Z Dвизначає площина розсіяння, яка, у свою чергу, задається орієнтацією вхідної щілини спектрографа (в даному випадку площина XZ). Відповідно до виду тензора нелінійної поляризуемости (4) константа нелінійної взаємодії рівна:
![]() (5)
(5)
Це означає, що реєструвалося випромінювання, розсіяне на звичайних поляритонах.
§2. Розсіяння світла на поляритонах в умовах нелінійної дифракції
Зміна нелінійній сприйнятливості в просторі надає дію на протікання параметричного процесу в кристалі. Періодична модуляція нелінійної сприйнятливості впливає на умови просторового синхронізму[6]:
 , (6)
, (6)
де ![]() - вектор оберненої гратки, пов'язаний з шарами-доменами, d - товщина шаруючи
- вектор оберненої гратки, пов'язаний з шарами-доменами, d - товщина шаруючи ![]() - одиничний вектор, перпендикулярний шарам, m - ціле число. Умови тимчасового синхронізму при цьому не міняються. Ефективна нелінійна сприйнятливість (5) може бути розкладена у вигляді(ceff(2)º):
- одиничний вектор, перпендикулярний шарам, m - ціле число. Умови тимчасового синхронізму при цьому не міняються. Ефективна нелінійна сприйнятливість (5) може бути розкладена у вигляді(ceff(2)º):
![]() (7)
(7)
Амплітуди просторових гармонік квадратичної сприйнятливості мають вигляд:
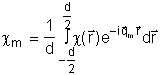 (8)
(8)
Тоді поляризація на частоті розсіяного випромінювання виглядає таким чином:
![]() (9)
(9)
Звідси видно, що інтенсивність розсіяного випромінювання в напрямі, відповідному m-ому порядку дифракції, пропорційна Фурье-амплітуді cm.
Нелінійна дифракція дозволяє отримати нове рівняння просторового синхронізму при генерації другої гармоніки. У роботі [7] досліджували генерацію другої гармоніки (ВГ) в неоднорідному кристалі ніобіту барії-натрію. Прослідкувала температурна залежність інтенсивності ВГ при нелінійній дифракції світла в околиці сегнетоэлектрического фазового переходу. Вище за температуру цього переходу доменів немає, тому інтенсивність ВГ різко падає, не опускаючись до нуля, оскільки існує залишкова поляризована шарів.
У роботі [6] отримані спектри нелінійної дифракції в полідоменном кристалі ніобіту барії-натрію при параметричному розсіянні світла. При цьому вектор нормалі шарів ![]() був перпендикулярний вектору накачування
був перпендикулярний вектору накачування ![]() . Спостерігалося розсіяння в першому і другому порядку дифракції, зміщеного по куту щодо нульового порядку дифракції. По отриманих спектрах визначено відхилення напряму зростання шарів від оптичної осі кристала і період регулярної доменної структури .
. Спостерігалося розсіяння в першому і другому порядку дифракції, зміщеного по куту щодо нульового порядку дифракції. По отриманих спектрах визначено відхилення напряму зростання шарів від оптичної осі кристала і період регулярної доменної структури .
У роботі [8] отримані одночасно в одному кристалі друга і третя гармоніки випромінювання 1,064 мкм. При генерації другої гармоніки в рівняння хвилевих векторів входив хвилевий вектор нелінійної дифракції першого порядку (m=1), а при генерації третьої гармоніки - третього порядку (m=3). Кристал складався з ділянок з періодичними доменами різної товщини. У кожному процесі брала участь область з доменами, товщина яких задовольняла рівнянню просторового синхронізму.
§3. Експериментальна установка для спостереження СПР
Основними елементами експериментальної установки (рис.3) для отримання спектрів спонтанного параметричного розсіяння на поляритонах (ПР-спектрограф) є: аргоновий лазер (1) з довжиною хвилі lL=488нм, нелінійний кристал (6), дві призми Глана (поляризатор (5) і аналізатор (6)), трьох лінзова оптична система (8) для отримання кутового спектру і спектрограф (10) для отримання частотного спектру.
Випромінювання лазера після направляючих дзеркал (2) проходить через діафрагми (3); накачування, що служать для контролю положення. Далі поляризатор (5) виділяє поляризацію накачування, паралельну щілині спектрографа. Аналізатор (6) пропускає сигнальну хвилю з поляризацією, перпендикулярній виділеній поляризації накачування. Інтерференційний фільтр (9) затримує випромінювання накачування, що залишилося.
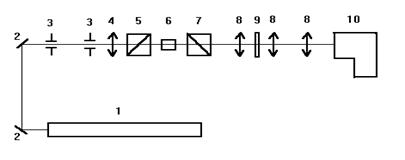
Мал.3. Оптична схема для спостереження параметричного розсіяння.
1. Ar+лазер; 2. Дзеркало ; 3. Діафрагма ; 4. Довгофокусна лінза ; 5. Призма Глана (поляризатор) ; 6. Зразок (кристал) ; 7. Призма Глана (аналізатор) ; 8. Трьохлінзова система ; 9 Інтерференційний фільтр ; 10. Спектрограф.
Розділ 2. Дослідження характеристик однорідних і шаруватих кристалів ніобіту літію з різним змістом домішок методом спектроскопії СПР
§1. Зразки кристалів LiNbO3
Досліджувалися кристали ніобіту літію з різною концентрацією домішок (Табл.1). Кристал ніобіту літію - одноосний негативний у видимій області спектру, такий, що має велике двопромінепреломлення Dn=ne-no-0.1. Концентрація домішок (Nd і Mg) була зміряна за допомогою рентгенівського мікроаналізу. Однорідні кристали No.4,5,6 вирощені уздовж оптичної осі Z.
Шаруваті кристали No.2,3 мали форму паралелепіпеда. Домішка неодиму практично не впливає на значення показників заломлення. Шари паралельні грані ![]() . Оптична вісь розташована в площині ZY під кутом 57о до нормалі шарів. Кристали ніобіту літію з обертальними шарами зростання і закріпленими на них доменами вирощують шляхом витягування з розплаву. У зразках ніобіту літію з періодичною доменною структурою варіювалася концентрація магнію від шару до шару, відповідно від шару до шару мінявся показник заломлення на малу величину, Dn10-4~ [10]. Для вирощування моно доменних кристалів, які мають шари з одно направленим вектором спонтанної поляризації, прикладають невелику напругу до зразка.
. Оптична вісь розташована в площині ZY під кутом 57о до нормалі шарів. Кристали ніобіту літію з обертальними шарами зростання і закріпленими на них доменами вирощують шляхом витягування з розплаву. У зразках ніобіту літію з періодичною доменною структурою варіювалася концентрація магнію від шару до шару, відповідно від шару до шару мінявся показник заломлення на малу величину, Dn10-4~ [10]. Для вирощування моно доменних кристалів, які мають шари з одно направленим вектором спонтанної поляризації, прикладають невелику напругу до зразка.
ТАБЛИЦЯ 1.
| Кристал LiNbO3 No. | Концентрація магнію. NMg,масс.% | Концентрація неодима. NNd,масс.% |
| 1 | 0 | 0 |
| 2 | 0.33 | 0.31 |
| 3 | 0.41 | 0.32 |
| 4 | 0.68 | 0 |
| 5 | 0.79 | 0 |
| 6 | 1.04 | 0 |
§2 Показники заломлення кристалів у видимому і інфрачервоному діапазоні спектру випромінювання
0 комментариев