Коэффициент собственности (независимости)

1.  Коэффициент собственности (независимости)

 

Соб.ср-ва (стр.490)_______ (1)

 Кс = Общ.велич.ср-в пр-тия (стр.700)

Особое значение этот показатель имеет для инвесторов и кредиторов. Средний его показатель равен 0,7. Если Кс ниже этого значения, то финансовая устойчивость ставится под сомнение.

13631,66___

Кс2007 = 303631,66 = 0,05

17440,09___

Кс2008 = 477440,09 = 0,04

В нашем случае, финансовая устойчивость предприятия ставится под сомнение, о чем, несомненно, должно знать руководство компании Б.

Рассчитаем коэффициент соотношения заемных и собственных средств или коэффициент структуры капитала:

Заем.ср-ва (стр.590 + 690) (2)

Кск = Собств. ср-ва (стр.490)

Кск показывает сколько заемных средств приходится на 1 руб. собственности. За критический показатель принимают 1 (50х50), а если показатель меньше 1, то финансовая устойчивость ставится под сомнение.

_290000,00_

Кск 2007 = 13631,66 = 21,27

_460000,00_

Кск 2008 = 17440,09 = 26,38

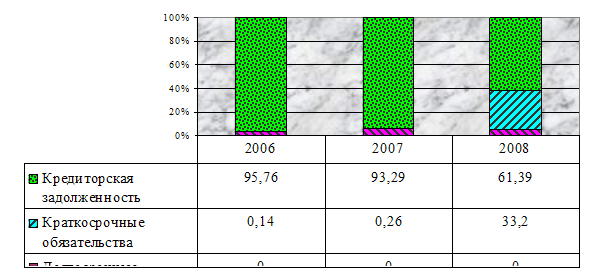
В нашем случае, в 2007 году на 1 руб. собственности приходилось 21 руб. 27 коп. заемных средств, в 2008 году этот показатель увеличивается на 5 руб. 11 коп. Можно сделать вывод, что в структуре капитала компании Б преобладают на текущий момент заемные средства и существует тенденция к росту этой части капитала. Необходимо также понимать, что это делает кампанию финансово зависимой от внешних источников финансирования и финансово неустойчивой.

Задача 3

Компания намерена финансировать программу расширения своего производства стоимостью 4 млн. долл. и рассматривает три возможных варианта:

а) эмиссию долговых обязательств под 14 % годовых;

б) эмиссию привилегированных акций с выплатой 12 % дивидендов;

в) эмиссию обыкновенных акций по цене 16 долл. за акцию.

В настоящее время в балансе компании зафиксированы долговые обязательства на 4 млн. долл. под 17 % годовых и 750 000 обыкновенных акций. Налог на прибыль – 24 %.

Если в настоящее время прибыль до уплаты процентов и налога составляет 1,65 млн. долл., то какую величину составит чистая прибыль на обыкновенную акцию по трем вариантам при условии, что прибыльность тотчас же не увеличится и сохранится на прежнем уровне?

Постройте график безразличия по всем вариантам и проанализируйте его.

Решение:

 

Метод, который будет применен для выбора наиболее желательного портфеля, использует так называемые кривые безразличия (indifference curves). Эти кривые отражают отношение инвестора к риску и доходности и, таким образом, могут быть представлены как двухмерный график, где по горизонтальной оси откладывается риск, мерой которого является стандартное отклонение (обозначенное s_p), а по вертикальной оси — вознаграждение, мерой которого является ожидаемая доходность (обозначенная r_p).

Рисунок представляет собой график кривых безразличия гипотетического инвестора. Каждая кривая линия отображает одну кривую безразличия инвестора и представляет все комбинации портфелей, которые обеспечивают заданный уровень желаний инвестора. Например, инвесторы с кривыми безразличия, изображенными на рисунке, будут считать портфели А и В (те же самые портфели, что и в таблице из предыдущего параграфа равноценными, несмотря на то, что они имеют различные ожидаемые доходности и стандартные отклонения, так как оба этих портфеля лежат на одной кривой безразличия I₂. Портфель В имеет большее стандартное отклонение (20%), чем портфель А (10%), и поэтому он хуже с точки зрения этого параметра. Однако полное возмещение этой потери дает выигрыш за счет более высокой ожидаемой доходности портфеля В (12%) относительно портфеля А (8%). Этот пример позволяет понять первое важное свойство кривых безразличия: все портфели, лежащие на одной заданной кривой безразличия, являются равноценными для инвестора.

 

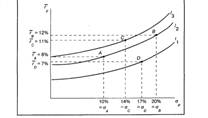
Рис. 1. График кривых безразличия инвестора, избегающего риска

Следствием этого свойства является тот факт, что кривые безразличия не могут пересекаться. Для того чтобы увидеть это, предположим, что две кривые в действительности пересекаются так, как это показано на следующем рисунке. Здесь точка пересечения обозначена X. При этом нужно учесть, что все портфели на кривой I₁, являются равноценными. Это означает, что они все так же ценны, как и X, потому что Х находится на I₁. Аналогично все портфели на I₂, являются равноценными и в то же время такими же ценными, как и X, потому что Х также принадлежит кривой I₂. Исходя из того, что Х принадлежит обеим кривым безразличия, все портфели на I₁ должны быть настолько же ценными, насколько и все портфели на I₂. Но это приводит к противоречию, потому что I₁ и I₂ являются двумя разными кривыми, по предположению отражающими различные уровни желательности. Таким образом, для того чтобы противоречия не существовало, кривые не должны пересекаться.

Хотя инвестор, представленный на первом рисунке, сочтет портфели А и В равноценными, он найдет портфель С с ожидаемой доходностью 11% и стандартным отклонением 14% более предпочтительным по сравнению с А и В. Это объясняется тем, что портфель С лежит на кривой безразличия I₃, которая выше и левее чем I₂. Таким образом, портфель С имеет большую ожидаемую доходность, чем А, что компенсирует его большее стандартное отклонение и в результате делает его более привлекательным, чем портфель А. Аналогично портфель С имеет меньшее стандартное отклонение, чем В, что компенсирует его меньшую ожидаемую доходность и в результате делает его более привлекательным, чем портфель В. Это приводит ко второму важному свойству кривых безразличия: инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее.

В заключение следует заметить, что инвестор имеет бесконечное число кривых безразличия. Это просто означает, что, как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними. Как показано на последнем рисунке, на котором заданы кривые безразличия I₁ и I₂, можно построить третью кривую I*, лежащую между ними. Это также означает, что другая кривая безразличия может быть построена либо выше I₂, либо ниже I₁.

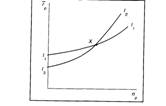
Рис. 2. Пересекающиеся кривые безразличия

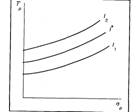
Рис. 3. Построение третьей кривой безразличия между двумя другими.

Здесь уместно спросить: как инвестор может определить вид его кривых безразличия? В конце концов, каждый инвестор имеет график кривых безразличия, которые, обладая всеми вышеперечисленными свойствами, в то же время являются сугубо индивидуальными для каждого инвестора. Один из методов, например, требует ознакомления инвестора с набором гипотетических портфелей вместе с их ожидаемыми доходностями и стандартными отклонениями. Из них он должен выбрать наиболее привлекательный. Исходя из сделанного выбора, может быть произведена оценка формы и местоположения кривых безразличия инвестора. При этом предполагается, что каждый инвестор будет действовать так, как будто бы он исходит из кривых безразличия при совершении выбора, несмотря на то, что осознанно их не использует.

В заключение можно сказать, что каждый инвестор имеет график кривых безразличия, представляющих его выбор ожидаемых доходностей и стандартных отклонений. Это означает, что инвестор должен определить ожидаемую доходность и стандартное отклонение для каждого потенциального портфеля, нанести их на график и затем выбрать один портфель, который лежит на кривой безразличия, расположенной выше и левее относительно других кривых. Как показано в этом примере, из набора четырех потенциальных портфелей - А, В, С и D - инвестор должен выбрать портфель С.

Задача 4

На протяжении последних десяти лет чистая прибыль в расчете на обыкновенную акцию (EPS) составила (в долл.):

1-й год	2-й год	3-й год	4-й год	5-й год	6-й год	7-й год	8-й год	9-й год	10-й год
1,70	1,82	1,47	1,92	2,18	2,32	1,83	2,23	2,50	2,73

Определите размер годовых дивидендов на одну акцию при использовании компанией следующих вариантов дивидендной политики:

а) поддержание коэффициента дивидендных выплат на постоянном уровне в 25%;

б) выплата регулярных дивидендов в размере 60 центов и выплата дополнительных дивидендов с целью вернуть коэффициент дивидендных выплат на уровне 40%, если его значение падает ниже этой величины;

 

Решение:

 

Проект А генерирует следующие денежные потоки : по годам 500, 400, 300, а проект В - 100, 300, 400, 600. Стоимость капитала проекта оценена на уровне 10%. Расчет дисконтированного срока осуществляется с помощью следующих таблиц.

Таблица 1.

Проект А (тыс. руб)

Год	0	1	2	3
Чистый денежный поток (ЧДП)	-1,000	500	400	300
Дисконтированный ЧДП	-1,000	455	331	225
Накопленный дисконтированный ЧДП	-1,000	-545	-214	11

В третьей строке таблицы помещены дисконтированные значения денежных доходов предприятия в следствии реализации инвестиционного проекта. В данном случае уместно рассмотреть следующую интерпретацию дисконтирования: приведение денежной суммы к настоящему моменту времени соответствует выделению из этой суммы той ее части, которая соответствует доходу инвестора, который предоставляется ему за то, что он предоставил свой капитал. Таким образом, оставшаяся часть денежного потока призвана покрыть исходный объем инвестиции. В четвертой строке таблицы содержатся значения непокрытой части исходной инвестиции. С течением времени величина непокрытой части уменьшается. Так, к концу второго года непокрытыми остаются только 214 тыс. руб., и поскольку дисконтированной значение денежного потока в третьем году составляет 225 тыс. руб., становится ясным, что период покрытия инвестиции составляет два полных года и какую-то часть года. Более конкретно для проекта получим:

.

Аналогично для второго проекта расчетная таблица и расчет дисконтированного периода окупаемости имеют следующий вид.

Таблица 2.

Проект В (тыс. руб.)

Год	0	1	2	3
Чистый денежный поток (ЧДП)	-1,000	100	300	400
Дисконтированный ЧДП	-1,000	91	248	301
Накопленный дисконтированный ЧДП	-1,000	-909	-661	-360

.

На основе результатов расчетов делается вывод о том, что проект А лучше, поскольку он имеет меньший дисконтированный период окупаемости.

Существенным недостатком метода дисконтированного периода окупаемости является то, что он учитывает только начальные денежные потоки, именно те потоки, которые укладываются в период окупаемости. Все последующие денежные потоки не принимаются во внимание в расчетной схеме. Так, если бы в рамках второго проекта в последний год поток составил, например 1000 тыс. руб., то результат расчета дисконтированного периода окупаемости не изменился бы, хотя совершенно очевидно, что проект станет в этом случае гораздо более привлекательным.

Задача 5

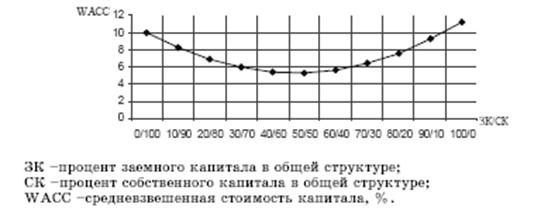
Рассчитайте средневзвешенную цену капитала (WACC) компании, если структура ее источников такова:

Источник средств	Доля в общей сумме источников	Цена
Акционерный капитал	70%	8.0%
Долгосрочные долговые обязательства	30%	7.5%

Как изменится значение показателя WACC, если доля акционерного капитала снизится до 60%?

 

Решение

 

Данная схема имеет следующие особенности:

·  в качестве показателя дисконта при оценке NPV проекта используется взвешенная средняя стоимость капитала (WACC) проекта,

·  в процессе принятия решения на основе IRR-метода значение внутренней нормы доходности проекта сравнивается с WACC,

·  при прогнозе денежных потоков не учитываются процентные платежи и погашение основной части кредитной инвестиции.

Согласно третьей особенности прогноз денежных потоков производится согласно схеме, представленной в таблице 1.

Таблица 1 –

Прогноз денежных потоков по традиционной схеме (тыс. руб).

	1 год	2 год	3 год	4 год	5 год
Чистая прибыль до амортизации, процентов	4880	5320	5900	5760	4790
и налога на прибыль
минус амортизация	976	1064	1180	1152	958
Чистая прибыль до налогов	3904	4256	4720	4608	3832
минус налог на прибыль	936,96	1021,44	1132,8	1105,92	919,68
Чистая прибыль	2967,04	3234,56	3587,2	3502,08	2912,32
Добавки: амортизация	976	1064	1180	1152	958
высвобождение рабочего капитала	0	0	0	0	0
остаточная стоимость оборудования	7510	7447,75	7385,5	7323,25	7261
Дополнительные денежные потоки в связи с изменением рабочего капитала	0	0	0	0	0
Чистые денежные потоки	11453,04	11746,31	12152,7	11977,33	11131,32

Прокомментируем некоторые положения данной расчетной схемы.

1.  Амортизация добавляется к чистой прибыли, так как не является денежным видом издержек и включается в валовые издержки для целей установления налога на прибыль.

2.  Под “высвобождением рабочего капитала” понимается объем инвестиций в оборотные средства предприятия, связанные с увеличением дебиторской задолженности и товарно-материальных запасов, которые к концу проекта ликвидируются, что приводит к дополнительному положительному денежному потоку. Понятно, что этот денежный поток появляется только в последний год таблицы.

3.  Остаточная стоимость оборудования также квалифицируется как положительный денежный поток в последний год проекта, так как допускается, что оборудование будет продано по остаточной стоимости или будет использовано для целей другого проекта.

4.  Дополнительные денежные потоки в связи с изменением рабочего капитала появляются в том случае, когда основные статьи оборотных средств предприятия (дебиторская задолженность и товарно-материальные запасы) и краткосрочных обязательств (кредиторская задолженность) изменяются в процессе реализации проекта. Это является, главным образом, следствием изменения объема реализации предприятия. Действительно, если объем реализации увеличивается согласно проекту на 10 процентов, то пропорционально этому увеличивается дебиторская задолженность. Например, дебиторская задолженность предприятия увеличилась в течение года с 50,000 руб. до 62,000. Это означает, что долг предприятию со стороны клиентов возрастает на 12,000, т.е. предприятие не дополучит 12,000 руб. Следовательно, такое изменение квалифицируется, как отрицательный денежный поток. Такое же положение имеет место для изменения статьи “товарно-материальные запасы”. Увеличение кредиторской задолженности, наоборот, соответствует увеличению денежного потока.

Возникает естественный вопрос: почему при расчете денежного потока не были учтены процентные платежи и погашение основной части долга. Дело в том, что дисконтирование денежных потоков производится в соответствии с показателем дисконта, равным взвешенной средней стоимости капитала (в которую в качестве одной из компонент входит стоимость долга) и все дисконтированные денежные потоки при определении показателя NPV сравниваются с общей суммой инвестиций (в которую в качестве одной из компонент входит кредитная доля совокупности финансовых ресурсов, привлеченных для проекта). Напомним, что процесс дисконтирования и последующее сравнение с исходной инвестицией при оценке показателя NPV соответствует вычитанию из денежных потоков дохода инвесторов (прямых и кредитных) и сопоставлению современных значений денежных потоков с исходным объемом инвестиций (прямых и кредитных). Таким образом, если бы мы вычли процентные платежи и выплату основной части долга при прогнозе денежных потоков, мы тем самым учли бы долговую компоненту дважды: один раз в прямом виде в таблице прогнозов денежных потоков, а другой раз в процессе дисконтирования и вычисления NPV.

Расчетная схема для оценки эффективности инвестиций приобретает законченный вид.