Навигация
Определить среднюю многолетнюю величину (норму) годового стока при наличии данных наблюдений
17763
знака
8
таблиц
3
изображения
1. Определить среднюю многолетнюю величину (норму) годового стока при наличии данных наблюдений.
Исходные данные: среднегодовые расходы воды, рассчитываемый период 10 лет (с 1964 – 1973 гг.).
Qо=
,
где Qi– средний годовой стока за i-й год;
n – число лет наблюдений.
Qi=994,3
Qо= 
=99,43м3/с (величина среднего многолетнего стока).
Полученную норму в виде среднего многолетнего расхода воды требуется выразить через другие характеристики стока: модуль, слой, объем и коэффициент стока.
Модуль стока Мо=
= 
=3,56 л/с*км2, где F – площадь водосбора, км2.
Средний многолетний объем стока за год:
Wo=Qo*T=99,43*31,54*106=3 136,022 м3,
где Т – число секунд в году, равное приблизительно 31,54*106 с.
Средний многолетний слой стока ho=
=
=112,4мм/год
Коэффициент стока α=
=
=0,165,
где хо – средняя многолетняя величина осадков в год, мм.
2. Определить коэффициент изменчивости (вариации) Сvгодового стока.
Сv=
, где
– среднеквадратическое отклонение годовых расходов от нормы стока.
= 
.
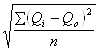Если n<30, то= 
.
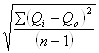Если сток за отдельные годы выразить в виде модульных коэффициентов к=
, то Сv=
, а при n<30 Сv=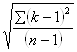
Составим таблицу для подсчета Сvгодового стока реки.
Таблица 1
Данные для подсчета Сv
| № п/п | Годы | Годовые расходы м3/с | Qo | к= | К-1 | (к-1)2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1964 | 125,00 | 99,43 | 1,26 | 0,26 | 0,066 |
| 2 | 1965 | 102,00 | 99,43 | 1,03 | 0,03 | 0,001 |
| 3 | 1966 | 83,90 | 99,43 | 0,84 | -0,16 | 0,024 |
| 4 | 1967 | 67,90 | 99,43 | 0,68 | -0,32 | 0,101 |
| 5 | 1968 | 112,00 | 99,43 | 1,13 | 0,13 | 0,016 |
| 6 | 1969 | 105,00 | 99,43 | 1,06 | 0,06 | 0,003 |
| 7 | 1970 | 151,00 | 99,43 | 1,52 | 0,52 | 0,269 |
| 8 | 1971 | 101,00 | 99,43 | 1,02 | 0,02 | 0,000 |
| 9 | 1972 | 67,00 | 99,43 | 0,67 | -0,33 | 0,106 |
| 10 | 1973 | 79,50 | 99,43 | 0,80 | -0,20 | 0,040 |
| Всего: | 994,30 | 10,00 | 0,00 | 0,627 | ||
Сv==
= 
= 0.2638783=0.264.
Относительная средняя квадратическая ошибка средней многолетней величины годового стока реки за период с 1964 по 1973 гг. (10 лет) равна:
= 
=
= 8,3%
Относительная средняя квадратическая ошибка коэффициента изменчивости Сvпри его определении методом моментов равна:
=23,24%.
Длина ряда считается достаточной для определения Qoи Cv, если 
5-10%, а 
10-15%. Величина среднего годового стока при этом условии называется нормой стока. В нашем случае находится в пределах допустимого, а 
больше допустимой ошибки. Значит, ряд наблюдений недостаточный необходимо удлинить его.
Похожие работы
... 551,20 9 993,06 1 661,86 17 785,72 -3 572,66 -13 565,72 -5 234,53 К= W/U = 2,97 Wср= 228,02 6. Расчет водохранилища многолетнего регулирования. Многолетнее регулирование проектируется в случае, когда годовая отдача с учетом потерь превышает ...
... , и лишь высокогорные участки Кыргызского хребта имеют холодный тундровый тип климата.3. Сток и его распределение 3.1 Определение нормы годового стока и его статистических характеристик Нормой годового стока Q0 называется среднее его значение за многолетний период такой продолжительности, при увеличении которой полученное среднее существенно не меняется, включающий несколько полных четных ...
... и максимальный сток, величина минимального стока определяется главным образом величиной и характером грунтового питания рек. Поэтому рассмотрим влияние подстилающей поверхности на основную характеристику стока—его среднее многолетнее значение — норму. Почвы как элемент географического ландшафта имеют зональное распределение. Различные почвы обладают неодинаковыми воднофизическими свойствами и, в ...
... П, мм 90 90 90 90 126 129 110 95 90 90 90 90 П, млн., м 0.54 0.54 0.54 0.54 0.76 0.77 0.66 0.57 0.54 0.54 0.54 0.54 П = 0,001* П * w, (млн. м3) По данным этой таблицы чертится график (рис. 2.) 2. Расчет водохранилища сезонно-годового регулирования стока балансовым методом 2.1 Установление режима работы водохранилища Расчет регулирования по методу прямой задачи ...
0 комментариев