Навигация
По знайденим l, k обчислити нові значення елементів таблиці по формулам (1.11)
3. по знайденим l, k обчислити нові значення елементів таблиці по формулам (1.11)
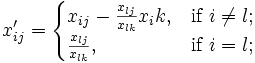
![]() ,
,
де ![]() та перейти до виконання операції (1.2) з новими значеннями всіх xij = x'ij.
та перейти до виконання операції (1.2) з новими значеннями всіх xij = x'ij.
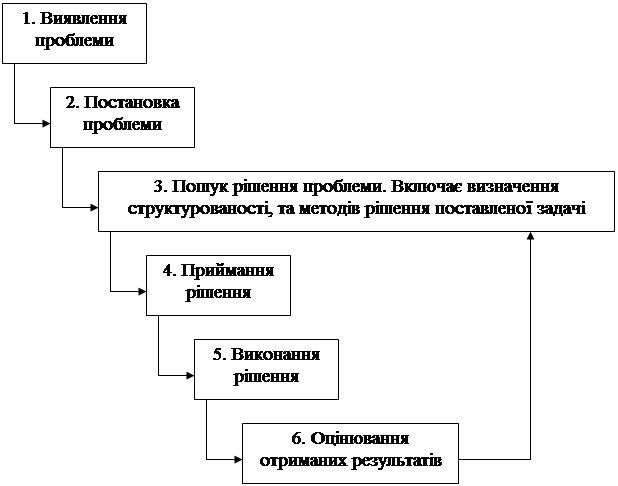
Перетворення (12) замінює вектор коефіцієнтів Xk = (x1k, …, xmk) на одиничний вектор Xk з xlk = 1. В силу монотонного збільшення x0 повернення до вже пройденого плану неможливе, а із скінченності кількості опорних планів випливає скінченність алгоритму. Початковий опорний план з одиничним базисом можна отримати, розв'язавши описаним алгоритмом допоміжну задачу
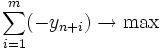 ,
,
при обмеженнях
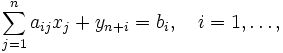
![]() ;
;
![]() ,
,
яка містить одиничний базис, який складається із векторів An+1, …, An+m. Цим векторам відповідають штучні змінні із значеннями ![]() , i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі
, i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі 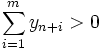 , вихідна задача не має розв'язку. Якщо ж
, вихідна задача не має розв'язку. Якщо ж 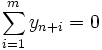 та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які по формулам (1.11) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних
та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які по формулам (1.11) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних ![]() дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин bi на bi + εi, де εi достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.
дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин bi на bi + εi, де εi достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.
Задача
Мається Аi постачальників вантажу (I = 1…m) та Bj споживачів цього вантажу (j = 1…n). Запаси вантажу у постачальників, попит споживачів та вартість перевезення одиниці вантажу від і – го постачальника до j – го споживача Cij у г.о. надані в таблиці. Належить скласти такий план перевезення вантажу, який забезпечив би мінімальні транспортні витрати.
Таблиця 1. – Вхідні дані до транспортної задачі
| Постачаль- ники | Запаси вантажу | Споживачі та їх попит | |||
| В1=15 | В2=25 | В3=18 | В4=12 | ||
| А1 | 25 | 2 | 4 | 3 | 6 |
| А2 | 18 | 3 | 5 | 7 | 5 |
| А3 | 12 | 1 | 8 | 4 | 5 |
| А4 | 15 | 4 | 3 | 2 | 8 |
Економіко – математична модель задачі:
Цільова функція:
Z = 2X11 + 4X12 + 3X13 + 6X14 + 3X21 + 5X22 +7X23 + 5X24 + X31 + 8X32 + 4X33 + 5 X34 + 4 X41 + 3 X42 + 2 X43 + 8 X44 – min.
Обмеження:
X11 +X12 +X13 +X14 = 25,
X21 +X22 +X23 +X24 = 18,
X31 +X32 +X33 +X34 = 12,
X41 +X42 +X43 +X44 = 15,
X11 +X21 +X31 +X41 = 15,
X12 +X22 +X32 +X42 = 25,
X13 +X23 +X33 +X43 = 18,
X14 +X24 +X34 +X44 = 12,
Xij >= 0.
2. Розрахунок задачі лінійного програмування на ПК
Сутність транспортної задачі полягає в тому, щоб забезпечити мінімальні транспортні витрати перевезень вантажу від постачальників до споживачів (цільова функція), і при цьому вантаж від постачальників має бути вивезеним (обмеження на спроможність постачальників), а потреби споживачів – задоволені (обмеження на потреби споживачів).
Рішення транспортної задачі на ПК проводиться за таким алгоритмом.
1. Оформити шапку та заголовки рядків і стовпців у Exel.
2. Заповнити електронну таблицю: блоки «Запаси.», «Споживання» та «Матриця вартості».
3. Записати формулу цільової функції за допомогою Мастера функций, для чого:
3.1 натиснути на кнопку fx панелі інструментів Стандартная, ініціювати Мастер функцій;
3.2 вибрати функцію Математическая / СУММПРОИЗВ;
3.3 встановити курсор у полі Матриця вартості, відмітити відповідний блок та зафіксувати перший аргумент функції;
3.4 встановити курсор у полі Матриця рішення, відмітити відповідний блок та зафіксувати другий аргумент функції;
3.5 закінчити запис формули, клацнувши ОК.
4. В клітинках блоків Формули обмежень за запасами та Формули обмежень за споживанням записуються формули сумування змінних відповідно за запасами постачальників та потребою споживачів.
5. З’в'язати електронну таблицю з вікном «Поиск решения», для чого
5.1 відмітити клітинку «Цільова функція», відкрити вікно «Поиск решения»;
5.2 заповнити рядок «Установить целевую ячейку»;
5.3 встановити режим «Равной» у стан «Минимальному значению»
5.4 заповнити рядок «Изменения ячейки» посиланням на блок «Матриця рішення»;
5.5 Заповнити вікно «Ограничения» обмеженнями за рядками та стовпцями змінних, що відповідає запасам постачальників та потрабам споживачів;
5.6 у рядку «Знак» вибрати знак відношення розглядаємої транспортної задачі (>=, <=, =);
5.7 заповнення рядків вікна «Добавить» закінчити натиском кнопки ОК;
5.8 Натиснувши кнопку «Параметры», встановити у вікні «Параметры поиска решения» режим «Линейная модель» та «Неотрицательные значения»; натиснути кнопку ОК.
6. Ініціювати рішення задачі, натиснувши кнопку «Выполнить».
Таблиця 2. - Рішення задачі за допомогою Exel
| Транспортна задача | ||||||
| Матриця вартості | ||||||
| 2 | 4 | 3 | 6 | |||
| 3 | 5 | 7 | 5 | |||
| 1 | 8 | 4 | 5 | |||
| 4 | 3 | 2 | 8 | |||
| Матриця рішень | Запаси | |||||
| 0 | 22 | 3 | 0 | 25 | 25 | |
| 3 | 3 | 0 | 12 | 18 | 18 | |
| 12 | 0 | 0 | 0 | 12 | 12 | |
| 0 | 0 | 15 | 0 | 15 | 15 | |
| 15 | 25 | 18 | 12 | Цільова функція | ||
| 15 | 25 | 18 | 12 | 223 | ||
| Споживання | ||||||
Висновки
Таким чином, представлена в даній розрахунково–економічній роботі транспортна задача вирішена із застосуванням комп’ютерної програми Ms Excel. Цей метод дає можливість знайти оптимальний план перевезень товару, щоб при цьому затрати були мінімальними.
Описана у роботі задача про оптимальні перевезення і метод її рішення – тільки окремий приклад великої множини задач лінійного програмування. Мета транспортної задачі – розробка найбільш раціональних шляхів і способів транспортування товарів, ліквідація надмірно далеких, зустрічних та повторних перевезень. Усе це скорочує час просування товарів, зменшує затрати підприємств, пов’язані з здійсненням процесів постачання сировини, матеріалів, палива, обладнання тощо.
Перелік посилань
1. Гончаренко Л.С. Оформлення матеріалів самостійної роботи студентів: Навчальний посібник. – Херсон: МІБ, 1999. – 50 с.
2. Лугинин О.Е., Белоусова С.В., Львов М.С. Єкономико – математические методы и модели: Учебное пособие. – Херсон: МИБ, 1998. – 212 с.
3. Лугінін О.Є., Білоусова С.В., Білоусов О.М.. Економетрія: Навчальний посібник. – Херсон: МІБ, 2002. – 251 с.
4. Лук’яненко І.Г., Красикова Л.І. Економетрика: Підручник. – К.: Товариство «Знання» КОО, 1998. – 212 с.
5. Методичні вказівки до самостійної роботи студентів усіх форм навчання при вивченні дисципліни «Економетрія» / Укл. О.Є. Лугінін. – Херсон: МІБ, 2000.- 25 с.
Похожие работы
... the building of a Safe Regional Environment. - Kiev (Ukraine). - 2004. - P. 194-198. - 0,3 друк. арк. (особистий внесок - 60%, модель, результати, пропозиції). АНОТАЦІЯ Пешко О.В. Економіко-математичні моделі управління інвестиційним портфелем. - Рукопис. Дисертація на здобуття наукового ступеня кандидата економічних наук за спеціальністю 08.03.02 - економіко-математичне моделювання. - Киї ...
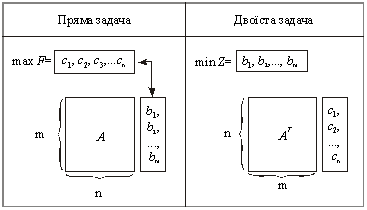
... виокремлюють певні підкласи. Наприклад, ігри двох осіб із нульовою сумою. Наведену класифікацію використано для структурування курсу «Математичне програмування». 2. Економічна інтерпретація прямої та двоїстої задач лінійного програмування Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари таких задач розглянемо ...
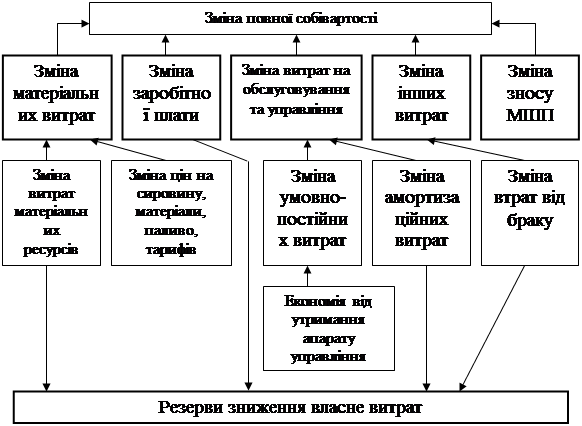
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
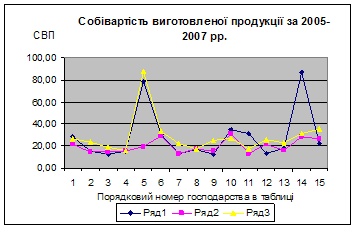
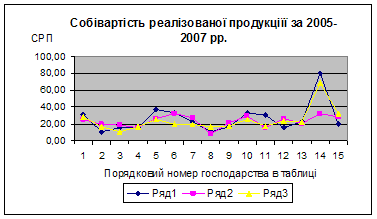
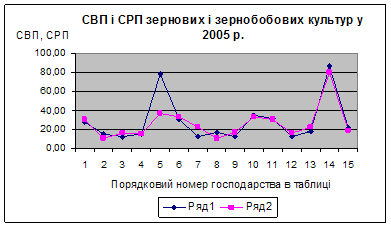
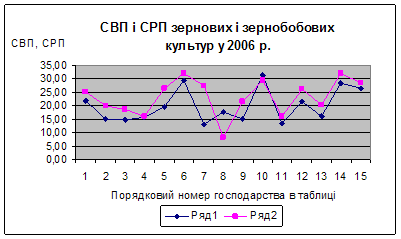
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...

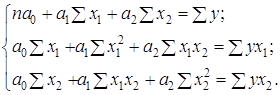
0 комментариев