Федеральное агентство по образованию Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кумертауский филиал
Кафедра ТОЭ
Расчетно-графическая работа №1
дисциплина «Теоретические основы электротехники»
тема: ИССЛЕДОВАНИЕ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Кумертау 2009
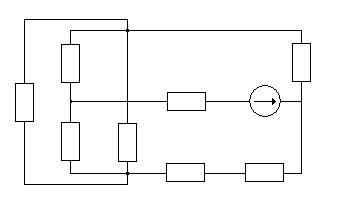
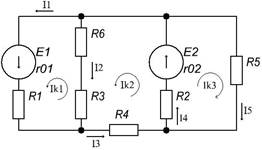
Расчет методом контурных токов.
Преобразуем источник тока в эквивалентный ему источник ЭДС
Рассчитаем собственные токи
I1 = I11 - Jк2
I2 = I33 - I11
I3 = I22 - I11
I4 = I22
I5 = I33 – I22
I6 = I33
EJk2 = Jк2 ∙R1 = -2 ∙ 90 = -180 В
![]()
![]()
(1) ![]()
![]()
Рассчитаем собственные сопротивления контуров и сопротивления, находящиеся на границе контуров:
R11 = R1 + R2 + R3 =90+80+80 = 250 Ом
R22 = R3 + R4 + R5 =80+30+50 = 160 Ом
R33 = R2 + R5 + R6 =80+40+50 = 170 Ом
R12 = R21 = - R3 = -80 Ом
R23 = R32 = - R2 = -50 Ом
R13 = R31 = - R5 = -80 Ом
Рассчитаем сумму Э.Д.С. действующих в контуре:
E11 = E1+EJk2 = -230 В
E22 = 0
E33 = E6 = 400 B
Cоставим матрицы сопротивлений и Э.Д.С.:
Рассчитываем матрицу с помощью программы Gauss, находим контурные токи I11, I22, I33. Рассчитываем собственные токи.
I11 = 0,3035 А
I22 = 1,026 А
I33 = 2,7976 А
I1 = I11 - Jк2 = 0,3035+2 = 2,3035 А
I2 = I33 - I11 =2,7976-0,3035 = 2,4941 А
I3 = I22 - I11 =1,026-0,3035 = 0,7225 А
I4 = I22 =1,026 А
I5 = I33 – I22 =2,7976-1,026 = 1,7716 А
I6 = I33 =2,7976 А
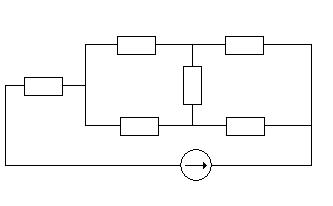
Расчет методом узловых потенциалов
j4 = 0
Рассчитаем собственные токи
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2) ![]()
![]()
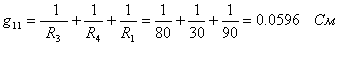
![]()
![]()
![]()
![]()
![]()
![]()
J22 = - 10 А
J33 = 0 А
Составим расширенную матрицу, состоящую из проводимостей и токов, решив ее с помощью программы Gauss найдем потенциалы узлов.
j1 = -257.3955 В j2 = -288.1563 В j3 = -199.5682 В
![]()
![]()
![]()
![]()
![]()
![]()
Полученные двумя методами токи сверим и сведем в таблицу 1
Таблица 1
| I1 | I2 | I3 | I4 | I5 | I6 | |
| МКТ | 2,3035 | 2,4941 | 0,7225 | 1,026 | 1,7716 | 2,7976 |
| МУП | 2,3044 | 2,4946 | 0,7228 | 1,0253 | 1,7717 | 2,7961 |
Баланс мощностей
![]()
![]()
Рист. ~ Рпотр. Баланс мощностей выполняется.
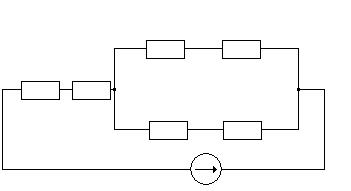
Расчет I1 методом эквивалентного генератора
Считаем напряжение холостого хода на зажимах 1-4
MУП:
![]()
![]()
(3) ![]()
![]()
Составим расширенную матрицу, состоящую из проводимостей и токов, решив ее с помощью программы Gauss найдем потенциалы узлов.
![]()
g11 g12 g13 E11
g21 g22 g23 E22
g31 g32 g33 E33
j1 = -369.2439 В j2 = -350.7677 В j3 = -258.4645 В
Е г = - j1
Uxx= Е г - Е1 = 319.2439 В
Рассчитаем входное сопротивление.
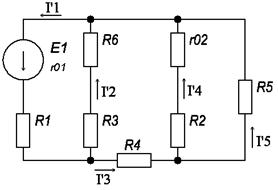
Преобразовываем схему, изображенную на рис 1.5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
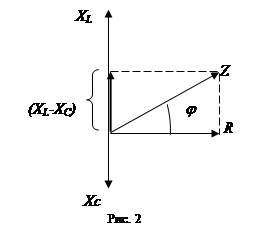
Потенциальная диаграмма контура 4-1’-1-2-4’-4.
j1 = -257.3955 В
j1’ = j4 – I1R1 = -207.3В
j2 = -288.1563 В
j4’ = j2 – I6R6 = - 400 В
Похожие работы
... неровностей на поверхности анода, т.е. происходит его полировка. 2 Расчётная часть 2.1Задание на курсовую работу Расчет разветвлённой электрической цепи постоянного тока. Для заданной электрической цепи необходимо: 1) Записать систему уравнений по законам Кирхгофа (без расчетов); 2) Определить все токи и ...
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
... 7. В выводе сравните между собой вычисленное и измеренное значение силы тока и сделайте вывод о выполнении закона Ома. Отчет по лабораторной работе № 1 Исследование цепи переменного тока. выполненной учащим…… школы «Поиск» …………………………………………………………………………………… «…..»……….. 200….г Задание 1. Предварительные расчеты и измерения Емкость конденсатора: С =……… мкФ =………´ 10-6 Ф Индуктивность ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...

0 комментариев