Давление пара в плите

1.5 Давление пара в плите

Внутреннее соединение в плите в горячем состоянии в момент выхода из пресса должно быть достаточно высоким для того, чтобы противостоять любому давлению пара, которое существует внутри плиты при открытии пресса. Относительно низкая температура в внутреннем слое плиты в обычных случаях не дает очень высокого давления пара. С повышением температуры во внутреннем слое там быстро увеличивается давление пара. Увеличение давления пара может вызвать расслаивание и вздутие.

Расслоение определяют как четкое расхождение частиц во внутреннем слое плиты. Это может быть результатом низких температур плит пресса, недостаточного давления, низкого качества связующего или сочетания этих факторов. Некоторые из этих факторов могут вызвать разнотолщинность. Вздутия в плите образуются, когда давление пара летучих продуктов (влаги, пара и других веществ) больше, чем сила внутреннего сцепления в плите. Вздутие обычно имеет место в центре плиты, так как в этой области плита наиболее слабая. Многие участки плиты могут иметь хорошее сцепление наряду с вздутиями в разных местах. Раньше причиной вздутия считали закупорку поверхностей пакета. Следует также отметить, что плотность и порода древесины и плотность плиты также могут быть причиной такого явления.

1.6 Время полного смыкания плит пресса, удельное давление и распределение плотности по толщине плиты (профиль плотности)

Один из самых важных факторов в определении свойств плит – время смыкания плит пресса. Это время тесно связано с содержанием влаги, а также с рядом других факторов. Время полного смыкания определяют как время, необходимое для уплотнения пакета до конечной толщины плиты, как только плиты пресса вступают в контакт с поверхностью пакета. Ряд профилей плотности можно получить в плите, изменяя эти факторы. Как только наступает дисбаланс температуры, давления или влагосодержания, профиль становится не симметричным, а сдвинутым. Такого явления следует избегать, так как это влияет на свойства плиты и плита коробится. Как только тепло от плит пресса начинает проникать в пакет, происходят два явления, определяющие конечный профиль плотности (наряду с давлением). Во-первых, передается тепло с наружных слоев к внутреннему. Во-вторых, влага превращается в пар, а пар смягчает древесные частицы и облегчает процесс сжатия. Такая пластификация сначала происходит на наружных слоях. С увеличением скорости смыкания плит пресса, когда пакет достиг почти конечной толщины (за 1 мин или меньше), мягкие наружные слои прессуются до большей плотности. Внутренний слой все еще холодный и сопротивляется давлению. Когда достаточное количество тепла достигает внутреннего слоя для его пластификации, наружные слои приобрели более высокую плотность и связующее отвердело, так что удерживает эти слои при большей плотности. При более медленном смыкании плит пресса требуется меньшее давление и, следовательно, меньшее сжатие в наружных слоях. Кроме того, связующее в наружных слоях может отверждаться до того, как произойдет уплотнение. Таким образом, наружные слои довольно жесткие. При более низкой плотности во время последующего этапа времени смыкания плит пресса происходит пластификация и уплотнение промежуточных и внутренних слоев, когда связующее еще жидкое. Профиль плотности может быть изменен предварительным прессованием. Предварительное прессование пакета до конечной толщины приводит к тому, что будут исключены колебания плотности по всей толщине плиты.

Качество поверхности плит можно улучшать повторным дополнительным прессованием при 371 0С в течение нескольких секунд. Такая высокая температура потребует дополнительного пресса, но зато не потребуется прикладывать столь высокое давление.

1.7 Предварительное и последующее отверждение связующего

Более низкая плотность плиты на ее пласти происходит, возможно, за счет полного отверждения связующего до достижения окончательной толщины плиты в процессе прессования. Большая часть этой более мягкой поверхности удаляется во время процесса шлифования. Мягкие поверхности связаны с предварительным отверждением или высыханием связующего, вызываемым в первый момент, когда горячие плиты пресса вступают в контакт с пакетом. При обычных температурах 163-191 0С отверждение связующего в наружном слое происходит почти мгновенно до того, как пакет уплотнен до конечной толщины. Хотя предварительное отверждение можно снять увеличением влажности наружного слоя, это может увеличить время прессования.

Вспомним относительно медленное смыкание плит в первых многоэтажных прессах для изготовления плит. Получали очень мягкие наружные поверхности и шлифованием снимали с наружных слоев до 3.2 мм. Многие многоэтажные прессы были модификацией прессов для производства фанеры, приспособленных для производства композиционных плит. Они смыкались снизу, что сначала закрывались нижние этажи, а потом верхние. В 16-этажном прессе это приводило к тому, что каждая плита имела различный профиль плотности, а следовательно, и различные свойства. Этот недостаток был ликвидирован в результате разработки системы одновременного смыкания плит пресса, так что все плиты прессуются идентично.

Последующее отверждение может быть и полезно и вредно. С одной стороны, оно выгодно для штабелирования в горячем состоянии плит с фенольным связующим; здесь отверждение заканчивается после выгрузки из пресса. С другой стороны, укладка плит в горячем состоянии с карбамидным связующим может привести к разрыву связей связующего в результате гидролиза, что вызывается воздействием температуры, влагосодержания и времени. Гидролиз происходит там, где молекулы связующего расщепляются, правда, по этому поводу существуют различные мнения. Одни считают, что такое явление происходит исключительно в древесине, так как она более чувствительна к потере прочности, другие считают, что разрыв происходит на плоскости соединения древесины со связующим.

Глава 2. Выбор и обоснование математической модели объекта

Выбрать модель означает выбрать вид функции. Данный этап самый ответственный. На данном этапе выбора вида модели экспериментатор должен располагать знаниями заранее проведенных исследований. На основании которых он может предположить о характере влияния фактора на параметрах процесса.

Полные и дробные факторные планы позволяют получить линейное описание зависимости отклика от каждого из варьируемых факторов. При детальном изучении большинства процессов лесопромышленных и деревообрабатывающих производств такое представление оказывается слишком грубым. В такой ситуации необходимо обратиться к экспериментальным планам второго порядка.

Планами второго порядка называют такие планы многофакторного эксперимента, с помощью которых можно получить математическое описание объектов в виде полиномов второго порядка. Для трех факторов соответствующее уравнение регрессии записывается в виде:

.

Эта модель содержит все слагаемые линейной модели: свободный член b0, линейные члены b1x1, b2x2, b3x3.

Также модель второго порядка включает квадратичные члены, являющиеся произведениями коэффициентов регрессии на квадраты двух различных факторов, т.е. члены вида b12x1x2, b13x1x3, b23x2x3. Зависимость выходной величины от каждого из факторов, полученная на основе квадратичной модели, представляется на графике отрезком параболы, имеющей ветви, направленные либо вверх, либо вниз. Позволяет достаточно полно описать широкий круг реальных зависимостей.

Глава 3. Выбор и составление плана эксперимента

К планам второго порядка относятся: В-планы и униформ-рототабельные планы (УРП).

В УРП опыты в угловых точках факторного пространства отсутствуют.

В В-планах второго порядка опыты поставлены в угловых точках факторного пространства, т.е. в условиях, когда все факторы принимают свои граничные значения. Это опыты вида .

В-планы синтезированы математиками, исходя из требований наибольшей точности оценок коэффициентов регрессии. В этих планах каждый фактор варьируется на трех уровнях: -1, 0, +1 в нормализованных обозначениях. В-планы обладают следующим свойством, называемым композиционностью. Составной частью В-плана является полный факторный план ПФП. Это свойство полезно в тех случаях, когда по результатам поставленного ПФП и ДФП получилась неадекватная модель. Тогда есть возможность дополнительно поставить некоторое число опытов, так что все опытов в целом образуют В-план 2-го порядка, а их обработка позволит получить соответствующую модель.

Назовем звездной точкой В-плана условия опыта, в котором один из факторов принимает нормализованное значение: +1 или –1, а остальные фиксируются на основном уровне – ноль в нормализованных обозначениях. Звездные точки для трех факторов (в нормализованных обозначениях):

При числе факторов k имеется 2k различных звездных точек.

В-план состоит из точек ПФП, к которым добавлено 2k звездных точек. Общее число опытов В-плана, таким образом, равно

.

В-план для трех варьируемых факторов в нормализованных обозначениях представлен в таблице 3.1

Таблица 3.1

Номер опыта	x1	x2	x3	y
1	+1	+1	+1	y1
2	+1	+1	-1	y2
3	+1	-1	+1	y3
4	+1	-1	-1	y4
5	-1	+1	+1	y5
6	-1	+1	-1	y6
7	-1	-1	+1	y7
8	-1	-1	-1	y8
9	+1	0	0	y9
10	-1	0	0	y10
11	0	+1	0	y11
12	0	-1	0	y12
13	0	0	+1	y13
14	0	0	-1	y14

В-план для трех варьируемых факторов в натуральных обозначениях представлен в таблице 3.2

Таблица 3.2

Номер опыта	x1	x2	x3	y
1	180	13	20
2	180	12	10
3	180	7	20
4	180	7	10
5	160	13	20
6	160	13	10
7	160	7	20
8	160	7	10
9	180	10	15
10	160	10	15
11	170	13	15
12	170	7	15
13	170	10	20
14	170	10	10

Глава 4. Проверка нормальности распределения выходной величины

Результаты предварительной серии опытов представлены в таблице 4.1

Таблица 4.1

9,342	9,199	9,356
9,221	9,303	9,224
9,324	9,84	9,495
9,085	9,439	10,07
8,718	9,606	9,651
9,583	10,192	9,818
9,501	9,208	9,931
9,839	9,562	9,553
10,657	10,115	9,7
9,965	10,007	9,642
10,054	8,111	9,775
9,992	8,482	9,323
10,019	9,664	9,213
9,898	9,253	11,085
9,039	8,962	9,418
9,596	9,611	8,921
9,183	9,946	9,941
9,909	9,714	9,365
9,47	9,567	8,959
9,239	9,179	9,043

Разобьем диапазон от 8,111 до 11,085 на интервалы равной длины. Для определения числа интервалов k воспользуемся формулой:

k = 1 + 3,2ln n, (4.1)

где n – объем выборки.

Значение k, найденное по формуле, округляем до ближайшего целого.

k = 1 + 3,2ln 60  7.

Длина каждого интервала:

 (4.2)

Предполагается, что выходная величина подчиняется нормальному закону распределения. Это предположение можно проверить разными способами. Наиболее строгим из них является применение критерия χ2 Пирсона. Для этого необходимо иметь выборку достаточно большого объема: n > 50 – 150. Диапазон изменения выходной величины в этой выборке разбивается на l интервалов так, чтобы эти интервалы покрывали всю ось от - до + и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количество mi наблюдений, попавших в каждый интервал. Затем вычисляют теоретические попадания случайной величины в каждый i-й интервал. Для этого используют формулу

pi = Ф(z2) – Ф(z1), где (4.3)

z1 = (- ) / s; z2 = ( - ) / s;

где  - среднее арифметическое выборки; s – среднее квадратическое отклонение выборки;  - нижняя граница i-го интервала;  - верхняя граница i-го интервала; Ф(z) – нормированная функция Лапласа:

Ф(z) =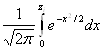

Значения ее для z = z1 и z = z2 определяют из таблиц. При отыскании значений этой функции для отрицательных значений аргумента следует иметь в виду, что функция Ф(z) нечетная:

Ф(- z) = - Ф(z).

Следующим этапом является вычисление величины χ2 по формуле

χ2 = . (4.4)

По выбранному уровню значимости q и числу степеней свободы k = l – 3 из таблицы отыскивают . Гипотезу о нормальности распределения можно принять, если .

Вычисления удобно вести заполняя таблицу:

Таблица 4.2

№ интервала			mi	z1	z2	Ф(z1)	Ф(z2)	pi	pin
1	2	3	4	5	6	7	8	9	10	11	12
1	8,111	8,537	2	-2,19	-2,06	0,014	0,019	0,005	0,3	2,89	9,633
2	8,537	8,963	3	-2,06	-1,18	0,019	0,119	0,1	6	9	1,5
3	8,963	9,389	19	1,18	-0,3	0,119	0,382	0,263	15,78	10,3684	0,657
4	9,389	9,815	18	-0,3	0,58	0,382	0,719	0,337	20,22	4,9284	0,244
5	9,815	10,241	16	0,58	1,46	0,719	0,927	0,208	12,48	12,3904	0,993
6	10,241	10,667	1	1,46	2,34	0,927	0,990	0,063	3,78	7,7284	2,045
7	10,667	11,093	1	2,34	3,22	0,990	0,999	0,009	0,54	0,2116	0,392

Данные выборки разобьем на 7 интервалов, границы которых указаны во втором и третьем столбцах. В четвертом столбце приведено количество наблюдений, попавших в каждый интервал. Далее по данным таблицы 4.1

вычислены среднее  и стандарт s выборки.

 = =

 =

=

=

=

= 9,535

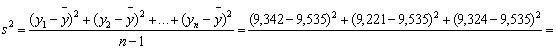
Среднее квадратическое отклонение:

 %

По формулам 4.3 рассчитываем значения z1 и z2 для каждого интервала (пятый и шестой столбец таблицы 4.2)

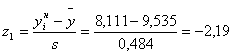
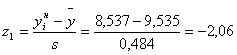
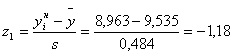
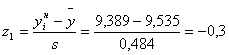
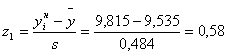
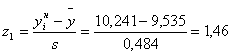
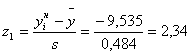
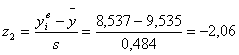
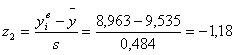
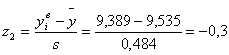
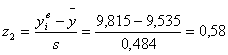
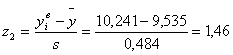
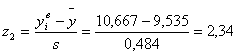
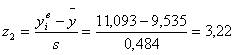
По таблице находим нормированную функцию Лапласа:

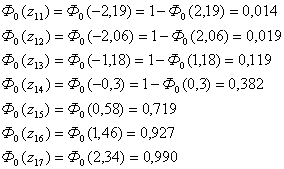
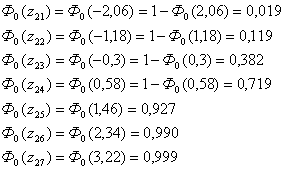
Согласно формуле (4.3) вычисляем теоретическое попадание случайной величины в каждый i-й интервал:

Искомую величину  получают суммированием значений последнего столбца . Выберем уровень значимости q = 0,05, число степеней свободы k = 7-3 = 4. По найденным величинам q и k из таблицы отыскиваем  - гипотеза о нормальности распределения отвергается.

Определение параметров генеральной совокупности

Математическое ожидание My определяется по формуле

Уровень значимости q = 1-P = 1 – 0,95 = 0,05

Число степеней свободы f = n – 1 = 60 – 1 = 59

Распределение Стьюдента tqf = 2,00

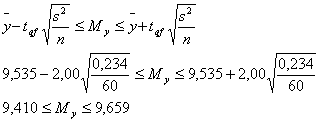
Глава 5. Расчет необходимого числа параллельных опытов

Исходными данными для этого расчета служат результаты серии опытов представлены в таблице 5.1

Таблица 5.1

9,342	9,199	9,356
9,221	9,303	9,224
9,324	9,84	9,495
9,085	9,439	10,07
8,718	9,606	9,651
9,583	10,192	9,818
9,501	9,208	9,931
9,839	9,562	9,553
10,657	10,115	9,7
9,965	10,007	9,642
10,054	8,111	9,775
9,992	8,482	9,323
10,019	9,664	9,213
9,898	9,253	11,085
9,039	8,962	9,418
9,596	9,611	8,921
9,183	9,946	9,941
9,909	9,714	9,365
9,47	9,567	8,959
9,239	9,179	9,043

Пусть требуется найти минимальное число n повторений опытов, при котором среднее арифметическое , найденное по этой выборке, отличалось бы от математического ожидания не более, чем на заданную величину ∆. Для ее решения необходимо знать оценку дисперсии s2. Искомое значение n определяется по формуле

 (5.1)

Величину t отыскивают из таблицы при уровне значимости q и числе степеней свободы f, связанном с оценкой дисперсии s2.

Глава 6. Обработка результатов эксперимента

Условия эксперимента и результаты дублированных опытов представлены в таблице 6.1

Таблица 6.1

Номер опыта	Нормализованные значения факторов			Результаты дублированных опытов
	x1	x2	x3	Y1	Y2	Y3	Y4
1	+	+	+	9,675	6,600	8,127	12,770	9,293	12,568	6,949
2	+	+	-	7,812	6,600	10,133	8,586	8,283	8,478	2,189
3	+	-	+	9,834	6,740	12,930	11,382	10,222	14,063	6,985
4	+	-	-	12,324	9,229	10,776	10,003	10,583	9,972	1,746
5	-	+	+	12,786	8,918	13,560	12,013	11,819	12,341	4,139
6	-	+	-	7,675	6,600	8,449	10,771	8,374	4,652	3,128
7	-	-	+	20,700	20,700	12,133	18,323	17,964	17,888	16,367
8	-	-	-	13,951	15,498	13,177	11,630	13,564	10,199	2,593
9	+	0	0	18,209	13,567	11,246	20,498	15,880	12,723	17,858
10	-	0	0	7,623	8,656	10,204	11,751	9,559	12,723	3,261
11	0	+	0	14,630	16,177	13,856	17,725	15,597	15,360	2,944
12	0	-	0	17,691	19,238	16,917	20,700	18,637	18,881	2,823
13	0	0	+	8,182	6,635	11,277	12,825	9,729	13,425	7,983
14	0	0	-	12,386	13,933	10,065	8,517	11,225	7,5357	5,787
Сумма								170,729		84,752

Расчет коэффициентов регрессии.

Для построения регрессионной модели по результатам В-плана нет необходимости обращаться к ЭВМ. Имеются формулы для статических оценок коэффициентов регрессии, пригодные для научного расчета. Они применимы для широкого класса планов, называемых симметричными к которым относятся и В-планы второго порядка. Коэффициенты регрессии для этих планов рассчитываются по формулам:

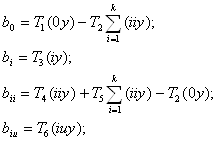
  (6.1)

где  - свободный член;

 - линейные коэффициенты регрессии, i = 1,2,…,k;

 - квадратичные коэффициенты регрессии, i = 1,2,…,k;

 - коэффициенты при парных взаимодействиях, ;

 - коэффициенты, значения которых указаны ниже.

В формулах (6.1) обозначено:

   (6.2)

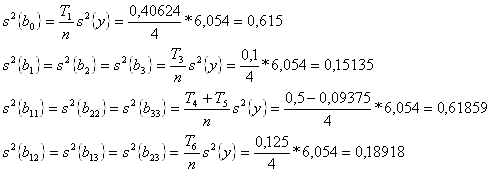
Значения коэффициентов  для В-планов с ПФП в ортогональной части с числом факторов k = 3 при отсутствии опытов в центре плана приведены в таблице 6.2:

Таблица 6.2

	Вид плана
	0,40624
	0,15624
	0,1
	0,5
	- 0,09375
	0,125

Число коэффициентов регрессии такого плана равно:

 (6.3)

В нашем случае, когда число факторов k = 3, число коэффициентов регрессии равно:

.

Средние арифметические по результатам каждой серии дублированных опытов:

Оценки дисперсий опытов:

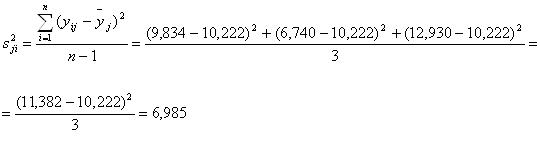
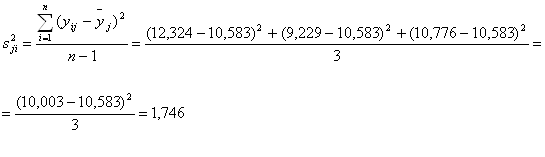
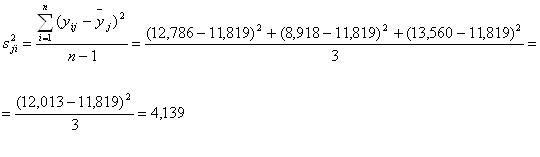
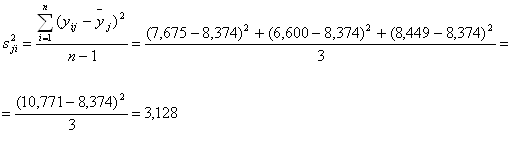
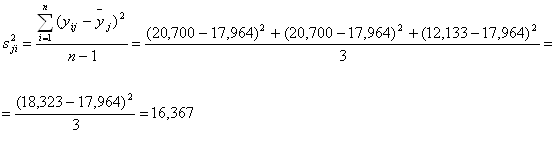
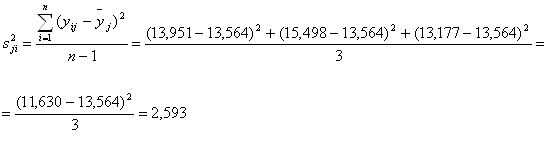
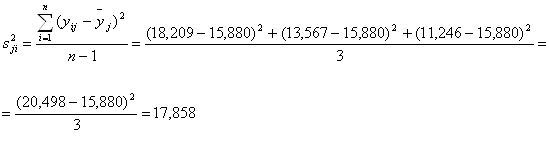
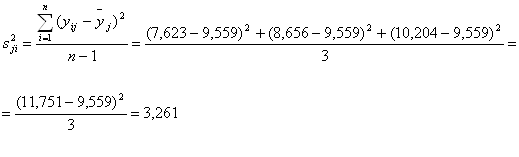
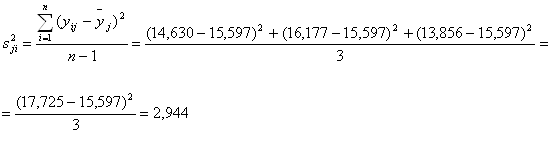
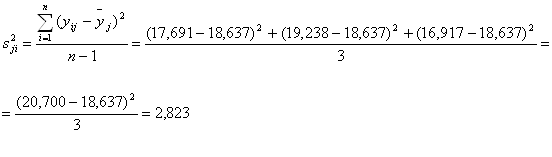
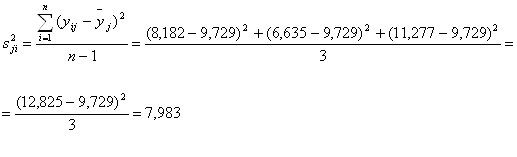
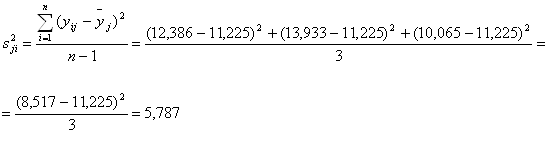
Проверка однородности дисперсий опытов по критерию Кохрена: для проверки однородности нескольких дисперсий при равных объемах всех рассматриваемых выборок может быть использован G-критерий Кохрена.

Пусть m – количество выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии . Вычисляется G-отношение по формуле

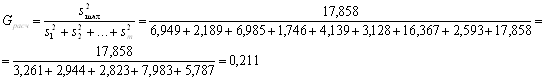
В числителе этой формулы стоит наибольшая из рассматриваемых дисперсий, а в знаменателе – сумма всех дисперсий. Далее обращаемся к таблицам распределения Кохрена. По выбранному уровню значимости q = 0,05, числу степеней свободы каждой выборки f = n - 1= 4 - 1 = 3 и по количеству выборок m = 14 из этой таблицы отыскивают величину G = Gтабл, Gтабл = 0,28. Gрасч < Gтабл - принимаем гипотезу об однородности дисперсий.

Оценка дисперсий воспроизводимости :

При вычислении коэффициентов регрессии по формуле 6.1 удобно воспользоваться таблицей 6.3:

Таблица 6.3

№	x1	x2	x3	x1x2	x1x3	x2x3
1	+1	+1	+1	+1	+1	+1	9,293	9,293	9,293	9,293	9,293	9,293
2	+1	+1	-1	+1	-1	-1	8,283	8,283	-8,283	8,283	8,283	8,283
3	+1	-1	+1	-1	+1	-1	10,222	-10,222	10,222	10,222	10,222	10,222
4	+1	-1	-1	-1	-1	+1	10,583	-10,583	-10,583	10,583	10,583	10,583
5	-1	+1	+1	-1	-1	+1	-11,819	11,819	11,819	11,819	11,819	11,819
6	-1	+1	-1	-1	+1	-1	-8,374	8,374	-8,374	8,374	8,374	8,374
7	-1	-1	+1	+1	-1	-1	-17,964	-17,964	17,964	17,964	17,964	17,964
8	-1	-1	-1	+1	+1	+1	-13,564	-13,564	-13,564	13,564	13,564	13,564
9	+1	0	0	0	0	0	15,880	0	0	15,880	0	0
10	-1	0	0	0	0	0	-9,559	0	0	9,559	0	0
11	0	+1	0	0	0	0	0	15,597	0	0	15,597	0
12	0	-1	0	0	0	0	0	-18,637	0	0	18,637	0
13	0	0	+1	0	0	0	0	0	9,729	0	0	9,729
14	0	0	-1	0	0	0	0	0	11,225	0	0	11,225
	-	-	-	-	-	-	-7,019	-17,604	29,448	115,541	124,336	111,056

№
1	9,293	9,293	9,293
2	8,283	-8,283	-8,283
3	-10,222	10,222	-10,222
4	-10,583	-10,583	10,583
5	-11,819	-11,819	11,819
6	-8,374	8,374	-8,374
7	17,964	-17,964	-17,964
8	13,564	13,564	13,564
9	0	0	0
10	0	0	0
11	0	0	0
12	0	0	0
13	0	0	0
14	0	0	0
	8,106	-7,196	0,416

Уравнение регрессии имеет вид:

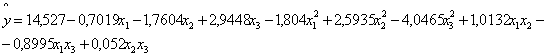
Оценки дисперсии коэффициентов регрессии определяется по формуле:

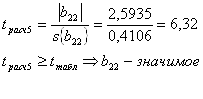
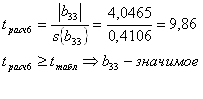
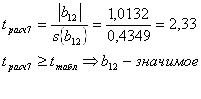
Оценка значимости коэффициентов регрессии.

Оценка значимости коэффициентов регрессии проверяется с помощью t-критерия Стьюдента. Из таблицы t-распределения по величине fy для уровня значимости q = 5 % берется табличное значение, tтабл = 2,02. Для каждого коэффициента регрессии bi вычисляется расчетное t-отношение:

 

где  - среднеквадратичное отклонение коэффициента , равное корню из его дисперсии. Проверяется условие . Коэффициенты регрессии, для которых это условие выполняется, являются незначимыми:

 

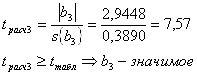
Уравнение регрессии имеет вид:

.

Затем вычисляем значения отклика по уравнению регрессии для каждого опыта:

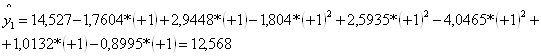
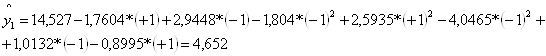
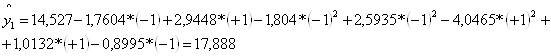
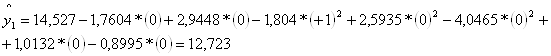
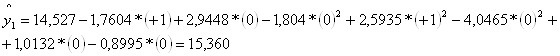
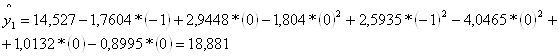
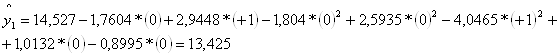
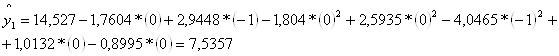
Проверка адекватности математической модели

После постановки опытов, вычисления коэффициентов регрессии и проверки их значимости приступают к проверке соответствия полученной модели результатам эксперимента. Такая проверка называется проверкой адекватности полученной модели.

Вычисляем сумму квадратов, характеризующую адекватность:

,

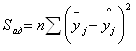где - число дублированных опытов в каждой серии;

 - усредненное по всем наблюдениям значение отклика в j-ом опыте;

 - значение выходной величины, рассчитанное по уравнению

регрессии.

Вычислим число степеней свободы

где N – число опытов;

P – число коэффициентов регрессии проверяемой модели, полученной

после отбрасывания незначимых коэффициентов регрессии.

Вычислим дисперсию адекватности:

, ()

С помощью F-критерия Фишера проверим однородность дисперсии адекватности и дисперсии воспроизводимости:

,

Далее сравним полученное значение  с табличным значением F-критерия , найденным при уровне значимости q = 5% для чисел степеней свободы  в числителе и  в знаменателе. ; , а следовательно, математическую модель можно считать не адекватной.

Глава 7. Интерпретация результатов эксперимента

Основываясь на построенной модели в нормализованных обозначениях факторов, необходимо построить три семейства графиков зависимости отклика от каждого из факторов .

Первое семейство: зависимость  от .