Навигация
Кредиты от коммерческого банка на жилищное строительство
Задание 1
Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).
Требуется:
1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a1=0,3; a2=0,6; a3=0,3.
2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной модели на основе исследования:
- случайности остаточной компоненты по критерию пиков;
- независимости уровней ряда остатков по d-критерию (критические значения d1 = 1,10 и d2 = 1,37) и по первому коэффициенту автокорреляции при критическом значении r1 = 0,32;
- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить на графике фактические, расчетные и прогнозные данные.
Таблица 1Поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 2 | 13 | 14 | 15 | 16 |
| Y(t) | 28 | 36 | 43 | 28 | 31 | 40 | 49 | 30 | 34 | 44 | 52 | 33 | 39 | 48 | 58 | 36 |
Решение
Будем считать, что зависимость между компонентами тренд-сезонный временный ряд мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
![]() , (1)
, (1)
где k – период упреждения;
Yр(t) — расчетное значение экономического показателя для t-гo периода;
a(t), b(t) и F(t) - коэффициенты модели; они адаптируются, уточняются по мере перехода от членов ряда с номером t-1 к t;
F(t+k-L) - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;
L - период сезонности (для квартальных данных L=4, для месячных – L=12).
Таким образом, если по формуле 1 рассчитывается значение экономического показателя, например за второй квартал, то F(t+k-L) как раз будет коэффициентом сезонности второго квартала предыдущего года.
Уточнение (адаптация к новому значению параметра времени t) коэффициентов модели производится с помощью формул:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Параметры сглаживания a1, a2 и a3 подбирают путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (т.е. чтобы обеспечить удовлетворительную адекватность и точность модели).
Из формул 1 - 4 видно, что для расчета а(1) и b(1) необходимо оценить значения этих коэффициентов для предыдущего период времени (т.е. для t=1-1=0). Значения а(0) и b(0) имеют смысл этих же коэффициентов для четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 1.
Для оценки начальных значений а(0) и b(0) применим линейную модель к первым 8 значениям Y(t) из табл. 1. Линейная модель имеет вид:
![]() . (5)
. (5)
Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения а(0) и b(0) по формулам 6 - 9:
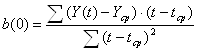 ; (6)
; (6)
![]() ; (7)
; (7)
![]() ; (8)
; (8)
![]() . (9)
. (9)
Применяя линейную модель к первым 8 значениям ряда из таблицы 1 (т.е. к данным за первые 2 года), находим значения а(0) и b(0). Составим вспомогательную таблицу для определения параметров линейной модели:
Таблица 2| t | Y(t) | t-tcp | Y-Ycp | (t-tcp)2 | (Y-Ycp)(t-tcp) | |
| 1 | 28 | -3,5 | -7,625 | 12,25 | 26,6875 | |
| 2 | 36 | -2,5 | 0,375 | 6,25 | -0,9375 | |
| 3 | 43 | -1,5 | 7,375 | 2,25 | -11,0625 | |
| 4 | 28 | -0,5 | -7,625 | 0,25 | 3,8125 | |
| 5 | 31 | 0,5 | -4,625 | 0,25 | -2,3125 | |
| 6 | 40 | 1,5 | 4,375 | 2,25 | 6,5625 | |
| 7 | 49 | 2,5 | 13,375 | 6,25 | 33,4375 | |
| 8 | 30 | 3,5 | -5,625 | 12,25 | -19,6875 | |
| S | 36 | 285 | 0 | 0 | 42 | 36,5 |
![]()
![]()
![]()
![]()
Уравнение (5) с учетом полученных коэффициентов имеет вид: Yp(t)=31,714+0,869·t. Из этого уравнения находим расчетные значения Yр(t) и сопоставляем их с фактическими значениями (табл. 3). Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности I-IV кварталов F(-3), F(-2), F(-1) и F(0) для года, предшествующего первому году, по которому имеются данные в табл. 1. Эти значения необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4) и других параметров модели Хольта-Уинтерса по формулам 1 - 4.
Таблица 3Сопоставление фактических данных Y(t) и рассчитанных по линейной модели значений Yp(t)
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y(t) | 28 | 36 | 43 | 28 | 31 | 40 | 49 | 30 |
| Yp(t) | 32,583 | 33,452 | 34,321 | 35,190 | 306,060 | 36,929 | 37,798 | 38,667 |
Коэффициент сезонности есть отношение фактического значения экономического показателя к значению, рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности I квартала F(-3) может служить отношение фактических и расчетных значений Y(t) I квартала первого года, равное Y(1)/Yр(1), и такое же отношение для I квартала второго года (т.е. за V квартал t=5) Y(5)/Yр(5). Для окончательной, более точной, оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин.
F(-3) = [ Y(1) / Yp(1) + Y(5) / Yp(5) ] / 2=[ 28 / 32,583 + 31 / 36,060 ] / 2 = 0,8595.
Аналогично находим оценки коэффициента сезонности для II, III и IV кварталов:
F(-2) = [Y(2) / Yp(2) + Y(6) / Yp(6) ] / 2 = 1,0797;
F(-1) = [Y(3) / Yp(3) + Y(7) / Yp(7) ] / 2 = 1,2746;
F(0) = [Y(4) / Yp(4) + Y(8) / Yp(8) ] / 2 = 0,7858.
Оценив значения а(0), b(0), а также F(-3), F(-2), F(-1) и F(0), можно перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул 1 - 4.
Из условия задачи имеем параметры сглаживания a1=0,3; a2=0,6; a3=0,3. Рассчитаем значения Yp(t), a(t), b(t) и F(t) для t=l.
Из уравнения 1, полагая что t=0, k=1, находим Yр(1):
![]() Из уравнений 2 - 4, полагая что t=1, находим:
Из уравнений 2 - 4, полагая что t=1, находим:
![]() ;
;
![]() ;
;
![]() .
.
Аналогично рассчитаем значения Yp(t), a(t), b(t) и F(t) для t=2:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t=3:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t=4:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t=5:
![]()
Обратим внимание на то, что здесь и в дальнейшем используются коэффициенты сезонности F(t-L), уточненные в предыдущем году (L=4):
![]() ;
;
![]() ;
;
![]() ;
;
Продолжая аналогично для, t = 6,7,8,…,16 строят модель Хольта-Уинтерса (табл. 4). Максимальное значение t, для которого можно находить коэффициенты модели, равно количеству имеющихся данных по экономическому показателю Y(t). В нашем примере данные приведены за 4 года, то есть за 16 кваралов. Максимальное значение t равно 16.
Таблица 4 Модель Хольта-Уинтерса| t | Y(t) | a(t) | b(t) | F(t) | Yp(t) | Абс.погр., E(t) | Отн.погр., % |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 31,71 | 0,87 | 0,7858 | ||||
| 1 | 28,0 | 32,58 | 0,87 | 0,8594 | 28,01 | -0,01 | 0,02 |
| 2 | 36,0 | 33,42 | 0,86 | 1,0782 | 36,11 | -0,11 | 0,32 |
| 3 | 43,0 | 34,11 | 0,81 | 1,2661 | 43,69 | -0,69 | 1,60 |
| 4 | 28,0 | 35,14 | 0,87 | 0,7924 | 27,44 | 0,56 | 1,99 |
| 5 | 31,0 | 36,03 | 0,88 | 0,8600 | 30,95 | 0,05 | 0,16 |
| 6 | 40,0 | 36,97 | 0,90 | 1,0805 | 39,80 | 0,20 | 0,51 |
| 7 | 49,0 | 38,11 | 0,97 | 1,2778 | 47,94 | 1,06 | 2,17 |
| 8 | 30,0 | 38,72 | 0,86 | 19 | 30,97 | -0,97 | 3,24 |
| 9 | 34,0 | 39,57 | 0,86 | 0,8596 | 34,04 | -0,04 | 0,11 |
| 10 | 44,0 | 40,51 | 0,88 | 1,0839 | 43,68 | 0,32 | 0,73 |
| 11 | 52,0 | 41,19 | 0,82 | 1,2687 | 52,90 | -0,90 | 1,73 |
| 12 | 33,0 | 42,07 | 0,84 | 0,7834 | 32,84 | 0,16 | 0,47 |
| 13 | 39,0 | 43,64 | 1,06 | 0,8800 | 36,88 | 2,12 | 5,43 |
| 14 | 48,0 | 44,58 | 1,02 | 1,0796 | 48,45 | -0,45 | 0,95 |
| 15 | 58,0 | 45,64 | 1,03 | 1,2700 | 57,85 | 0,15 | 0,25 |
| 16 | 36,0 | 46,45 | 0,97 | 0,7783 | 36,56 | -0,56 | 1,56 |
Для того чтобы модель была качественной уровни, остаточного ряда E(t) (разности Y(t)-Yp(t) между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватности). Для проверки выполнения этих условий составим таблицу 5.
Проверка точности моделиБудем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs{E(t)}, поделенное на фактическое значение Y(t) и выраженное в процентах 100%·abs{E(t)}/Y(t)) в среднем не превышает 5%. Суммарное значение относительных погрешностей (см. гр. 8 табл. 4) составляет 21,25, что дает среднюю величину 21,25/16 = 1,33%.
Следовательно, условие точности выполнено.
Таблица 5 Промежуточные расчеты для оценки адекватности модели| Квартал, t | Отклонение, E(t) | Точки поворота | E(t)2 | [E(t)-E(t-1)]2 | E(t)∙E(t-1) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | -0,01 | - | 0,00 | - | - |
| 2 | -0,11 | 0 | 0,01 | 0,01 | 0,00 |
| 3 | -0,69 | 1 | 0,48 | 0,33 | 0,08 |
| 4 | 0,56 | 1 | 0,31 | 1,56 | -0,38 |
| 5 | 0,05 | 1 | 0,00 | 0,26 | 0,03 |
| 6 | 0,20 | 0 | 0,04 | 0,02 | 0,01 |
| 7 | 1,06 | 1 | 1,13 | 0,74 | 0,22 |
| 8 | -0,97 | 1 | 0,95 | 4,14 | -1,03 |
| 9 | -0,04 | 0 | 0,00 | 0,87 | 0,04 |
| 10 | 0,32 | 1 | 0,10 | 0,13 | -0,01 |
| 11 | -0,90 | 1 | 0,80 | 1,49 | -0,29 |
| 12 | 0,16 | 0 | 0,02 | 1,11 | -0,14 |
| 13 | 2,12 | 1 | 4,49 | 3,85 | 0,33 |
| 14 | -0,45 | 1 | 0,21 | 6,62 | -0,96 |
| 15 | 0,15 | 1 | 0,02 | 0,36 | -0,07 |
| 16 | -0,56 | - | 0,32 | 0,50 | -0,08 |
| S | 0,88 | 10 | 8,88 | 21,98 | -2,27 |
Для того чтобы модель была адекватна исследуемому процессу, ряд остатков E(t) должен обладать свойствами случайности, независимости последовательных уровней, нормальности распределения.
Проверка случайности уровней. Проверку случайности уровней остаточной компоненты (гр. 2 табл. 5) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда E(t) сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр. 3 табл. 5 для этой строки ставится 1, в противном случае в гр. 3 ставится 0. В первой и последней строке гр. 3 табл. 5 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней.
Общее число поворотных точек в нашем примере равно р = 10.
Рассчитаем значение q:
![]() .
.
Функция int означает, что от полученного значения берется только целая часть. При N = 16
![]() .
.
Если количество поворотных точек р больше q, то условие случайности уровней выполнено. В нашем случае р = 10, q = 6, значит условие случайности уровней ряда остатков выполнено.
Проверка независимости уровней ряда остатков (отсутствия автокорреляции). Проверку проводим двумя методами:
1) по d-критерию Дарбина-Уотсона;
2) по первому коэффициенту автокорреляции r(1).
1) 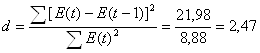 .
.
Примечание. В случае если полученное значение больше 2, значит, имеет место отрицательная автокорреляция. В таком случае величину d уточняют, вычитая полученное значение из 4. Находим уточненное значение d`=4-2,47=1,53
Полученное (или уточненное) значение d сравнивают с табличными значениями d1 и d2. Для нашего случая d1 =1,08, а d2=1,36.
Если 0<d<d1, то уровни автокоррелированы, то есть, зависимы, модель неадекватна.
Если d1<d<d2, то критерий Дарбина-Уотсона не дает ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней по первому коэффициенту автокорреляции).
Если d2<d<2 , то уровни ряда остатков являются независимыми.
В нашем случае d2<d`<2 , следовательно уровни ряда остатков являются независимыми.
2) 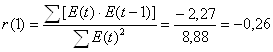
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения | r(1) | < rта6, то уровни ряда остатков независимы. Для нашей задачи критический уровень rта6 = 0,32. Имеем: | r(1) | = 0,26 < rтаб = 0,32 - значит уровни независимы.
Проверка соответствия ряда остатков нормальному распределению определяем по RS-критерию. Рассчитаем значение RS:
![]() ,
,
где Еmax - максимальное значение уровней ряда остатков E(t);
Emin - минимальное значение уровней ряда остатков E(t) (гр. 2 табл. 5):
S - среднее квадратическое отклонение.
Еmax=2,12, Emin=-0,97, Еmax-Emin= 2,12 - (-0,97) = 3,09;
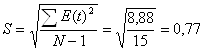
![]()
Полученное значение RS сравнивают с табличными значениями, которые зависят от количества точек N и уровня значимости. Для N=16 и 5%-го уровня значимости значение RS для нормального распределения должно находиться в интервале от 3,00 до 4,21.
Так как 3,00 < 4,02 < 4,21, полученное значение RS попало в заданный интервал. Значит, уровни ряда остатков подчиняются нормальному распределению.
Расчет прогнозных значений экономического показателяСоставим прогноз на четыре квартала вперед (т.е. на 1 год, с t=17 по t=20). Максимальное значение t, для которого могут быть рассчитаны коэффициенты a(t), b(t) определяется количеством исходных данных и равно 16. Рассчитав значения а(16) и b(16) (см. табл. 4), по формуле 1 можно определить прогнозные значения экономического показателя Yp(t). Для t=17 имеем:
![]()
Аналогично находим Yp(18), Yp(19), Yp(20):
![]()
![]()
![]()
Ha нижеприведенном рисунке проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения цены акции на 1 год вперед. Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.
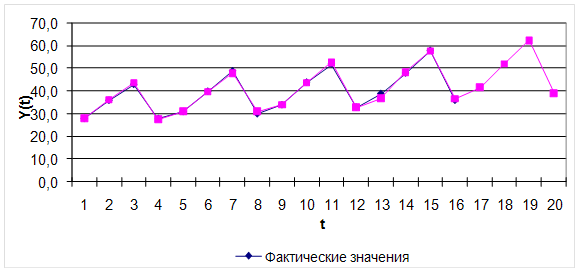
Рис. Сопоставление расчетных и фактических данных
Задание 2Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R, %К и %D.
Расчеты проводить для дней, для которых эти расчеты можно выполнить на основании имеющихся данных.
Таблица 6| Дни | Цены | ||
| макс. | мин. | закр. | |
| 1 | 998 | 970 | 982 |
| 2 | 970 | 922 | 922 |
| 3 | 950 | 884 | 902 |
| 4 | 880 | 823 | 846 |
| 5 | 920 | 842 | 856 |
| 6 | 889 | 840 | 881 |
| 7 | 930 | 865 | 870 |
| 8 | 890 | 847 | 852 |
| 9 | 866 | 800 | 802 |
| 10 | 815 | 680 | 699 |
Решение.
Экспоненциальная скользящая средняя (ЕМА). При расчете ЕМА учитываются все цены предшествующего периода, а не только того отрезка, который соответствует интервалу сглаживания. Однако последним значениям цены придается большее значение, чем предшествующим. Расчеты проводятся по формуле:
![]() ,
,
где k=2/(n+1), n – интервал сглаживания;
Ct – цена закрытия t-го дня;
ЕМАt – значения ЕМА текущего дня t.
Составим таблицу рассчитанных значений ЕМА:
Таблица 7| t | Цена закрытия, Ct | EMAt |
| 1 | 982 | - |
| 2 | 922 | - |
| 3 | 902 | - |
| 4 | 846 | - |
| 5 | 856 |
|
| 6 | 881 |
|
| 7 | 870 |
|
| 8 | 852 | 874,9926 |
| 9 | 802 | 850,6617 |
| 10 | 699 | 800,1078 |
Приведем алгоритм расчета.
1. Выбрать интервал сглаживания n (в нашем случае n = 5).
2. Вычислить коэффициент k (k= 2/(n + 1) = 2/(5 + 1) = 1/3).
3. Вычислить МА для первых 5 дней. Для этого сложим цены закрытия за первые 5 дней. Сумму разделим на 5 и запишем в графу ЕМАt за 5-ый день.
4. Перейти на одну строку вниз по графе ЕМАt. Умножить на k данные по конечной цене текущей строки.
5. Данные по ЕМАt за предыдущий день взять из предыдущей строки и умножить на (1- k).
6. Сложить результаты, полученные на предыдущих двух шагах. Полученное значение ЕМАt записать в графу текущей строки.
Похожие работы
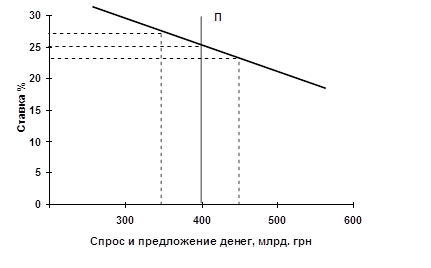
... станут доступнее, денежное предложение возрастет. Рост денежного предложения понизит процентную ставку, которая в свою очередь увеличит инвестиции и уровень ЧНП. РАЗДЕЛ 2 Экономический механизм начисления и взыскания процентов по кредитам в коммерческих банках 2.1 Плата за кредит и ее дифференциация. Порядок начисления и взыскания процентов по кредитам В условиях рыночных отношений ...
... теоретические основы кредитования, сущность, назначение и роль кредита, его формы, виды и функции, а также вопрос влияния на экономику ссудного процента. Во втором разделе будет проведен анализ порядка установления, начисления и взыскания процентов по кредитам на примере кредитного продукта «овердрафт» на основе данных по КБ «Приватбанк». 2. Анализ порядка установления, начисления и взыскания ...
... кредитования, правил выдачи и погашения ссуд, текущего наблюдения и анализа кредитных операций [12, 152] 2. Перспективы развития системы кредитования российскими коммерческими банками Кредитная политика, проводимая современными коммерческими банками, находится под влиянием многих факторов, определяемых особенностями экономической и политической ситуации в России. Под влиянием этих же ...
... собственных обязательств без риска неликвидности. Кроме того, кредитный рынок позволяет банку поддерживать высокую ликвидность своих средств продажей их на этом рынке. Кредитная политика коммерческого банка обеспечивает непрерывное использование всех средств, которые создаются для удовлетворения подлежащих погашению обязательств и минимального резерва ликвидности. Остаток средств необходимо ...



0 комментариев