Навигация
Вариационный размах - показывает, насколько велико различие между наибольшей и наименьшей единицами совокупности
10. Вариационный размах - показывает, насколько велико различие между наибольшей и наименьшей единицами совокупности
R = X max - X min=3,79
На основании полученных вычислений можно сделать следующие выводы:
1. Необходимое условие для того, чтобы выборка имела нормальный закон распределения, выполняется, т.к. для коэффициента вариации V выполняется неравенство:
V = 5,603735% < 33%
Отсюда следует, что все выборочные значения случайной величины X положительны, что мы и видим в исходных данных.
2. Для нормального распределения коэффициенты асимметрии и эксцесса должны быть равны нулю, т.е. Аs = Е = О
Выборочный коэффициент асимметрии служит для характеристики асимметрии распределения случайной величины. Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен 0.
По результатам вычисления асимметрия близка к нулю Аs = 0,069231.
В связи с этим необходимы дополнительные исследования для выяснения степени близости распределения выборки к нормальному распределению.
1.3 Результаты вычисления интервальных оценок для математического ожидания и дисперсии
Для вычисления интервальной оценки математического ожидания воспользуемся формулой:
![]()
Где a=M [X] - математическое ожидание,
N-1=V=59 - число степеней свободы,
![]() - величина, численно равная половине интервала, в который может попасть случайная величина
- величина, численно равная половине интервала, в который может попасть случайная величина ![]() , имеющая определённый закон распределения при заданной доверительной вероятности р и заданном числе степеней свободы V.
, имеющая определённый закон распределения при заданной доверительной вероятности р и заданном числе степеней свободы V.
Подставляем в формулу вычисленные ранее значения ![]() ,
,![]() и N. В результате получим
и N. В результате получим
16,0515 - t59,p (0,899484/√60) ‹a‹16,0515 + t59,p (0,899484/√60)
Задаёмся доверительной вероятностью ![]() ;
; ![]()
Для каждого значения ![]() (i=1,2) находим по таблице значения
(i=1,2) находим по таблице значения ![]() и вычисляем два варианта интервальных оценок для математического ожидания.
и вычисляем два варианта интервальных оценок для математического ожидания.
1. При ![]()
![]()
16,0515 - 2 (0,899484/√60) = 15,81925
16,0515 + 2 (0,899484/√60) = 16,28375
15,81925 < a < 16,28375
2.При ![]() t59; 0,99= 2,66
t59; 0,99= 2,66
16,0515 - 2,66 (0,899484/√60) = 15,74261
16,0515 + 2,66 (0,899484/√60) = 16,36039
15,74261 < a < 16,36039
Для интервальной оценки дисперсии существуют следующие неравенства:
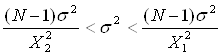
Подставляем в неравенство известные значения N и ![]() получим неравенство, в котором неизвестны
получим неравенство, в котором неизвестны ![]() и
и ![]() .
.
(59*0,809071) /Х22<σ2< (59*0,809071) / Х12
Задаваясь доверительной вероятностью ![]() (или уровнем значимости а) вычисляем значения
(или уровнем значимости а) вычисляем значения ![]() и
и ![]() . Используем эти два значения и степень свободы V=N-1 по таблице находим
. Используем эти два значения и степень свободы V=N-1 по таблице находим ![]() и
и ![]()
![]()
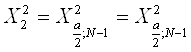
![]() и
и ![]() - это границы интервала, в который попадает случайная величина Х, имеющая
- это границы интервала, в который попадает случайная величина Х, имеющая ![]() распределение вероятности
распределение вероятности ![]() и заданной степени свободы V.
и заданной степени свободы V.
Для ![]() =0,95
=0,95
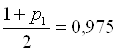
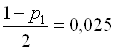 и V=59 находим по таблице:
и V=59 находим по таблице:
![]()
![]()
Подставляя в неравенства ![]() и
и ![]() и произведя вычисления, получим интервальную оценку:
и произведя вычисления, получим интервальную оценку:
(59*0,809071) /83,2976<σ2< (59*0,809071) / 40,4817
0,573068<σ2<1,179179
Для ![]()
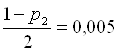 ;
; 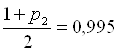 и V=59 находим по таблице:
и V=59 находим по таблице:
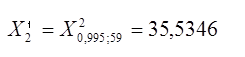 ,
, ![]()
Подставляя в неравенства ![]() и
и ![]() и произведя вычисления, получим интервальную оценку:
и произведя вычисления, получим интервальную оценку:
(59*0,809071) /91,9517<σ2< (59*0,809071) / 35,5346
0,519133<σ2<1,343343
Для интервальной оценки среднего квадратического отклонения имеем

При ![]()
![]()
σ = 0,899484
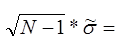
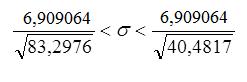 6,909064
6,909064
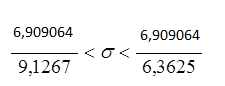
0,757017<σ<1,085904
При ![]()
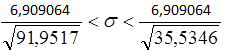
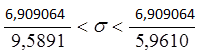
0,093802<σ< 0,368412
1.4 Результаты ранжирования выборочных данных вычисления моды и медианы
Используя исходные данные, записываем все заданные значения выборки в виде неубывающей последовательности значений случайной величины Х.
Таблица 1.4.1
Ранжированный ряд
| 1 | 14,4 | 11 | 15,15 | 21 | 15,61 | 31 | 15,88 | 41 | 16,4 | 51 | 17,02 |
| 2 | 14,44 | 12 | 15,15 | 22 | 15,64 | 32 | 15,93 | 42 | 16,4 | 52 | 17,12 |
| 3 | 14,85 | 13 | 15,22 | 23 | 15,68 | 33 | 15,96 | 43 | 16,52 | 53 | 17,26 |
| 4 | 15,01 | 14 | 15,22 | 24 | 15,7 | 34 | 16,05 | 44 | 16,6 | 54 | 17,36 |
| 5 | 15,02 | 15 | 15,26 | 25 | 15,78 | 35 | 16,26 | 45 | 16,62 | 55 | 17,38 |
| 6 | 15,03 | 16 | 15,28 | 26 | 15,8 | 36 | 16,29 | 46 | 16,67 | 56 | 17,39 |
| 7 | 15,04 | 17 | 15,31 | 27 | 15,81 | 37 | 16,3 | 47 | 16,75 | 57 | 17,7 |
| 8 | 15,07 | 18 | 15,38 | 28 | 15,81 | 38 | 16,31 | 48 | 16,84 | 58 | 17,78 |
| 9 | 15,1 | 19 | 15,41 | 29 | 15,85 | 39 | 16,38 | 49 | 16,91 | 59 | 17,94 |
| 10 | 15,12 | 20 | 15,59 | 30 | 15,86 | 40 | 16,38 | 50 | 16,91 | 60 | 18, 19 |
Интервал [14,40; 18, 19], содержащий все элементы выборки, разбиваем на частичные интервалы, используя при этом формулу Стерджесса для определения оптимальной длины и границ этих частичных интервалов.
По формуле Стерджесса длина частичного интервала равна:
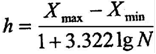 = 0,548717225
= 0,548717225
Для удобства и простоты расчетов округляем полученный результат до сотых: h = 0,55
За начало первого интервала принимаем значение:
Хо=Хmin - h/2 = 14,13
Х1=Х0 + h = 14,67
Х2 = Х1+h = 15,22
Х3 = Х2 + h = 15,77
Х4=16,32
Х5=16,87
Х6=17,42
Х7=17,97
Х8 = 18,52
Вычисление границ заканчивается как только выполняется неравенство
Хn >X max: Х8 = 18,52 > Хmax = 18, 19
По результатам вычислений составляем таблицу. В первой строке таблицы помещаем частичные интервалы, на второй строке - середины интервалов, в третьей строке записано количество элементов выборки, попавших в каждый интервал частоты, в четвертой строке записаны относительные частоты и в пятой строке записаны значения плотности относительных частот или значения выборочной, экспериментальной функции плотности (таблица 1.4.2).
Таблица 1.4.2
Значение выборочной функции и плотности
| Интервалы h
| [14,33; 14,67) | [14,67; 15,22) | [15,22; 15,77) | [15,77; 16,32) | [16,32,16,87) | [16,87; 17,42) | [17,42; 17,97) | [17,97; 18,52) |
|
| 14,40 | 14,95 | 15,50 | 16,05 | 16,59 | 17,14 | 17,69 | 18,24 |
| частота ni | 2 | 12 | 10 | 14 | 10 | 8 | 3 | 1 |
|
| 0,033333333 | 0,2 | 0,166666667 | 0,233333333 | 0,166666667 | 0,133333333 | 0,05 | 0,016666667 |
|
| 0,060747744 | 0,364486462 | 0,303738718 | 0,425234206 | 0,303738718 | 0,242990975 | 0,091121615 | 0,030373872 |
|
| 60,747744 | 364,486462 | 303,738718 | 425,234206 | 303,738718 | 242,990975 | 91,121615 | 30,373872 |
По результатам вычислений функции плотности, представленной в таблице 4.1 можно сделать вывод, что мода имеет один локальный максимум в окрестностях точки х=0.34 с частотой n=20.
Оценку медианы находим, используя вариационный ряд
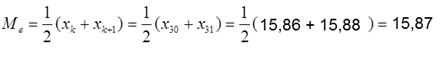
Т.к. N=2k, то k=N/2=30
![]() Сравнение оценок
Сравнение оценок ![]() медианы = 15,87 и оценки математического ожидания 16,0515 показывает, что они отличаются на 1,14 %.
медианы = 15,87 и оценки математического ожидания 16,0515 показывает, что они отличаются на 1,14 %.
1.5 Параметрическая оценка функции плотности распределения
Исходя из гипотезы, что заданная выборка имеет нормальный закон распределения, найдём параметрическую оценку функции плотности, используя формулу для плотности распределения вероятности нормального закона
![]()
где ![]() и
и ![]() известны - они вычисляются по выборке.
известны - они вычисляются по выборке.
![]() =0,899484
=0,899484
![]() =16,0515
=16,0515
Значения этой функции вычисляют для середин частичных интервалов вариационного ряда, т.е. при ![]() . На практике для упрощения вычислений функции
. На практике для упрощения вычислений функции ![]() , где i=1,2,…,k, пользуются таблицами значений функции плотности стандартной нормальной величины.
, где i=1,2,…,k, пользуются таблицами значений функции плотности стандартной нормальной величины.
![]()
Для этого вычисляем значения 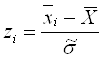 для i=1,2,…,k:
для i=1,2,…,k:



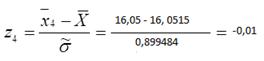
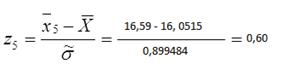

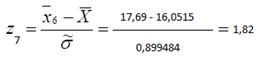 ,
, 
Затем по таблице находим значение
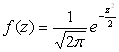 :
:
![]() 0,0775
0,0775
![]() 0,1895
0,1895
![]() 0,3271
0,3271
![]() 0,3986
0,3986
![]() 0,3230
0,3230
![]() 0,1804
0,1804
![]() 0,0694
0,0694
![]() 0,0184
0,0184
И после вычисляем функцию 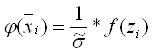 :
:
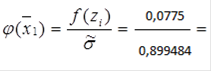 0,0862
0,0862
![]() 0,2107
0,2107
![]() 0,3637
0,3637
![]() 0,4431
0,4431
![]() 0,3591
0,3591
![]() 0, 2006
0, 2006
![]() 0,0772
0,0772
![]() 0,0205
0,0205
Функция ![]() , вычисленная при заданных параметрах
, вычисленная при заданных параметрах ![]() и
и ![]() в середине частичного интервала фактически является теоретической относительной частотой, отнесённой к середине частичного интервала
в середине частичного интервала фактически является теоретической относительной частотой, отнесённой к середине частичного интервала
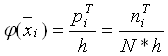
поэтому для определения теоретической частоты ![]() , распределённой по всей ширине интервала, эту функцию необходимо умножить на N*h.
, распределённой по всей ширине интервала, эту функцию необходимо умножить на N*h.
![]() , где h=0,55
, где h=0,55
![]() 0,55*0,0862= 0,0473
0,55*0,0862= 0,0473
![]() 0,1156
0,1156
![]() 0, 1995
0, 1995
![]() 0,2432
0,2432
![]() 0, 1970
0, 1970
![]() 0,1101
0,1101
p7T=0,0423
p8T=0,0112
![]() где N=60
где N=60
![]() 0,0473*60= 2,8367
0,0473*60= 2,8367
![]() 6,9361
6,9361
![]() 11,9726
11,9726
![]() 14,5896
14,5896
![]() 11,8225
11,8225
![]() 6,6030
6,6030
n7T=2,5402
n8T=0,6735
Результаты вычислений вероятностей и соответствующих частот приведены в таблице 5.1.
Таблица 1.5.1
|
|
|
|
|
|
|
|
|
|
| [14,33; 14,67) | 2 | 14,40 | 0,0333 | 0,0607 | -1,84 | 0,0862 | 0,0473 | 2,8367 |
| [14,67; 15,22) | 12 | 14,95 | 0,2 | 0,3644 | -1,23 | 0,2107 | 0,1156 | 6,9361 |
| [15,22; 15,77) | 10 | 15,50 | 0,1666 | 0,3037 | -0,62 | 0,3637 | 0, 1995 | 11,9726 |
| [15,77; 16,32) | 14 | 16,05 | 0,2333 | 0,4252 | -0,01 | 0,4431 | 0,2432 | 14,5896 |
| [16,32,16,87) | 10 | 16,59 | 0,1666 | 0,3037 | 0,60 | 0,3591 | 0, 1970 | 11,8225 |
| [16,87; 17,42) | 8 | 17,14 | 0,1333 | 0,2429 | 1,21 | 0, 2006 | 0,1101 | 6,6030 |
| [17,42; 17,97) | 3 | 17,69 | 0,05 | 0,0911 | 1,82 | 0,0772 | 0,0423 | 2,5402 |
| [17,97; 18,52) | 1 | 18,24 | 0,0166 | 0,0303 | 2,43 | 0,0205 | 0,0112 | 0,6735 |
|
| 60 | 1 | 0,9662 | 57,9742 |
Результаты вычисления экспериментальных и теоретических вероятностей и частот.
![]() 1
1
![]() 0,9662
0,9662
![]() 57,9742
57,9742
Из результатов вычислений следует, что сумма вероятностей в интервале [14,33; 18,52) равна единице, а сумма частот равна 57,9742. Это объясняется тем, что мы вычисляем вероятности в интервале, где заданы экспериментальные данные. Сравнение экспериментальных и теоретических частот по критерию Пирсона с целью проверки гипотезы о нормальном распределении возможно только в том случае, если для каждого частичного интервала выполняется условие ![]() . Результаты вычислений приведённые в таблице 5.1 показывают, что это условие выполняется не везде. Поэтому, те частичные интервалы, для которых частоты
. Результаты вычислений приведённые в таблице 5.1 показывают, что это условие выполняется не везде. Поэтому, те частичные интервалы, для которых частоты ![]() объединяем с соседними.
объединяем с соседними.
Соответственно объединяем и экспериментальные частоты ![]() .
.
Таблица 1.5.2
Теоретическая и экспериментальная плотности вероятности
|
| 0,0607 | 0,3644 | 0,3037 | 0,4252 | 0,3037 | 0,2429 | 0,0911 | 0,0303 |
|
| 0,0862 | 0,2107 | 0,3637 | 0,4431 | 0,3591 | 0, 2006 | 0,0772 | 0,0205 |
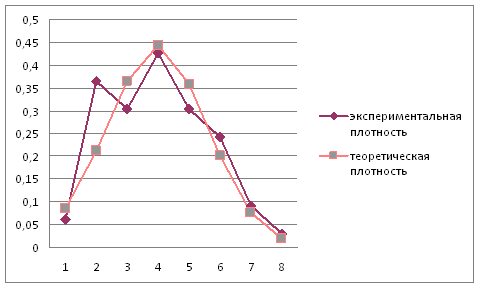
Рис.5.1 Теоретическая и экспериментальная плотности
1.6. Проверка гипотезы о нормальном распределении случайной величины по критерию Пирсона
Для проверки гипотезы о нормальном распределении случайной величины Х сравнивают между собой экспериментальные и теоретические частоты по критерию Пирсона:
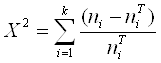
Статистика ![]() имеет распределение с V=k-r-1 степенями свободы, где число k - число интервалов эмпирического распределения, r - число параметров теоретического распределения, вычисленных по экспериментальным данным. Для нормального распределения число степеней свободы равно V=k-3.
имеет распределение с V=k-r-1 степенями свободы, где число k - число интервалов эмпирического распределения, r - число параметров теоретического распределения, вычисленных по экспериментальным данным. Для нормального распределения число степеней свободы равно V=k-3.
В теории математической статистики оказывается, что проверку гипотезы о модели закона распределения по критерию Пирсона можно делать только в том случае, если выполняются следующие неравенства: ![]()
![]() где i=1,2,3,… Из результатов вычислении, приведённых в таблице 5.1 следует, что необходимое условие для применения критерия согласия Пирсона не выполнены, т.к. в некоторых группах
где i=1,2,3,… Из результатов вычислении, приведённых в таблице 5.1 следует, что необходимое условие для применения критерия согласия Пирсона не выполнены, т.к. в некоторых группах ![]() . Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и, соответственно, уменьшают число групп, при этом частоты объединённых групп суммируются. Так объединяют все группы с частотами
. Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и, соответственно, уменьшают число групп, при этом частоты объединённых групп суммируются. Так объединяют все группы с частотами ![]() до тех пор, пока для каждой новой группы не выполнится условие
до тех пор, пока для каждой новой группы не выполнится условие ![]() .
.
При уменьшении числа групп для теоретических частот соответственно уменьшают и число групп для эмпирических частот. После объединения групп в формуле для числа степеней свободы V=k-3 в качестве k принимают
новое число групп, полученное после объединения частот.
Результаты объединения интервалов и теоретических частот для таблицы 5.1 приведены соответственно в таблице 6.1 Результаты вычислений из таблицы 6.1 можно используют для проверки гипотезы о нормальном распределении с помощью критерия Пирсона.
Таблица 1.6
Результаты объединения интервалов и теоретических частот.
|
|
|
|
|
|
|
| [14,33; 15,22) | 0,1629 | 9,7728 | 14 | 17,86922 | 1,828465 |
| [15,22; 15,77) | 0, 1995 | 11,9726 | 10 | 3,891151 | 0,325005 |
| [15,77; 16,32) | 0,2432 | 14,5896 | 14 | 0,347628 | 0,023827 |
| [16,32,16,87) | 0, 197 | 11,8225 | 10 | 3,321506 | 0,280948 |
| [16,87; 18,52) | 0,1636 | 9,8167 | 12 | 4,766799 | 0,485581 |
| сумма | 0,9662 | 57,9742 | 60 | 2,943825 |
Процедура проверки гипотезы о нормальном распределении случайной величины Х выполняется в следующей последовательности:
1. Задаёмся уровнем значимости ![]() или одним из следующих значений
или одним из следующих значений ![]() ,
, ![]() ,
, ![]() .
.
Похожие работы
... с денежной наличностью. Для определения потребности в наличных деньгах в целом по Российской Федерации, по регионам и по учреждениям банков и в соответствии с этим разработки мероприятий по стабилизации денежного обращения с 1991г. в РФ составляются прогнозы кассовых оборотов, в которых отражается объем и источники поступлений всех наличных денег в кассы банков, размеры и целевое направление их ...
... исследуемых объектов, приводит к изменению установившихся причинно-следственных связей. Именно поэтому изучение структуры и структурных сдвигов занимает важное место в курсе теории статистики. В статистике под структурой понимают совокупность единиц, обладающих определенной устойчивостью внутригрупповых связей при сохранении основных признаков, характеризующих эту совокупность как целое. Основные ...
... статистическую отчетность; в) бухгалтерскую отчетность и статистические формуляры. 2. Финансовый сектор экономики включает в себя: а) 3 подсектора; б) 4 подсектора; в) нет правильного ответа. 3. Статистика финансов выполняет такие функции: а) оперативная, управленческая, контрольная; б) оперативная, фиксирующая, аналитическая; в) оперативная, контрольная, аналитическая. 4. Статистика ...
... доходов( налоговые/неналоговые), расходов (текущие, капитальные вложения, кредиты) источники внутреннего и внешнего финансирования бюджета, классификация видов внутреннего и внешнего долга РФ 3. Статистика налогов и налогообложения. ) Налоги различают в зависимости от объекта налогообложения: Персональные (в зависимости от плательщика), Реальные- возникают в момент продажи имущества, ...
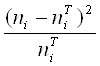


0 комментариев