Навигация
Статистическая проверка гипотез
Содержание
Введение Статистическая проверка гипотез 1.Статистическая гипотеза. Статистический критерий. Ошибки, возникающие при проверке гипотез2. Порядок проверки статистических гипотез
3. Проверка однородности результатов эксперимента в целях исключения грубых ошибок
4. Проверка гипотезы о воспроизводимости опытов
5. Проверка гипотезы о нормальном распределении ошибок эксперимента
6. Проверка гипотезы о виде распределения. ( Критерий согласия Пирсона )
6.1 Расчёт теоретических частот для нормального распределения
7.Проверка гипотезы о согласованности мнений экспертов (априорное ранжирование переменных)
8. Уравнение линейной регрессии. Коэффициент корреляции. Проверка гипотезы о значимости коэффициента корреляции
8.1 Метод наименьших квадратов 8.2 Проверка незначимости коэффициента корреляции 8.3 Использование корреляционной таблицы для вычисления коэффициента корреляцииВывод
Список литературы ПриложенияВведение
Тема курсовой работы «Статистическая проверка гипотез».
К важнейшим направлениям научно-технического прогресса относятся автоматизация производства, широкое применение компьютеров и роботов, создание гибких автоматизированных устройств и т.д. Во всех этих направлениях ведущая роль принадлежит электронике.
При создании электронной и электромеханической аппаратуры основные трудозатраты приходятся на ее настройку, снятие характеристик и испытания. При этом нередко используется малоэффективный традиционный метод однофакторного эксперимента, недостаточно внимания уделяется организации и планированию эксперимента и вероятностно-статистическому анализу получаемых данных. Чтобы повысить производительность труда в данной области, специалистам необходимо знать основы математической теории эксперимента и успешно применить ее на практике.
Цель работы – ознакомится со статистической проверкой гипотез, а именно:
о воспроизводимости результатов эксперимента, о виде распределения результатов эксперимента, о наличии корреляционных связей между факторами и переменной состояния и др., рассмотрении практических примеров.
Статистическая проверка гипотез 1. Статистическая гипотеза. Статистический критерий. Ошибки, возникающие при проверке гипотез
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известного распределения.
Например, гипотеза H0 - случайная величина распределена по нормальному закону.
Нулевой (основной) называется выдвинутая гипотеза H0.
Альтернативной (конкурирующей) называется гипотеза, противоречащая основной (конкурирующих гипотез может быть несколько).
Например, основная гипотеза - математическое ожидание случайной величины Y равно 5
H0 : My=5,
конкурирующие:
H1 : ![]()
H2 : ![]()
H3 : ![]()
Статистическим критерием (К) называется случайная величина, точное или приближённое распределение, которой известно и которая служит для проверки справедливости нулевой гипотезы.
Множество возможных значений критерия делится на две непересекающихся области:
1) значения, при которых нулевая гипотеза справедлива (область принятия гипотезы).
2) значения, при которых нулевая гипотеза отвергается (критическая область).
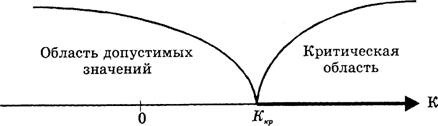
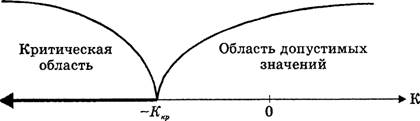
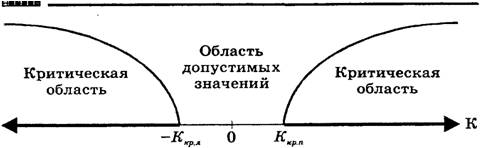
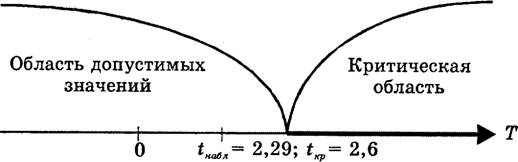
Критическая область может быть односторонней (левосторонней, правосторонней) или двусторонней.
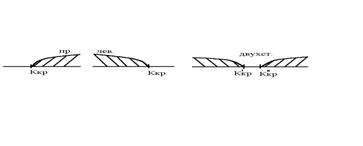
Рис.1. Виды критических областей: правосторонняя, левосторонняя и двусторонняя.
Точка Ккр, отделяющая критическую область от области принятия гипотезы, называется критической точкой.
Чтобы определить критическую область, выбирают число q-уровень значимости. q- вероятность того, что при справедливости нулевой гипотезы значение критерия К попадает в критическую область. Тогда для правосторонней критической области Ккр определяется из условия:
P { K > Kkp} = q.
Значение критерия табулировано, т. е. Kkp можно найти по таблице распределения критических точек в зависимости от уровня значимости q и числа степеней свободы f. -Наблюдаемое значение критерия Kнабл определяется по результатам эксперимента.
Если Kнабл<Kkp, то гипотеза H0 принимается. Если Kнабл>Kkp, то H0 отвергается, а принимается конкурирующая гинотеза H1.
Для левосторонней критической области критическая точка определяется из условия:
P { K < Kkp} = q.
Для двухсторонней:
P { K < K’kp} + P { K > K”kp} = q.
Если двусторонняя область симметрична относительно начала координат, то:
P { K < K’kp} = ![]() .
.
Так как наблюдаемое значение критерия определялось по результатам эксперимента, то Кнабл-случайная величина и, следовательно, могут возникать ошибки при принятии гипотезы. Различают ошибки первого и второго рода. К ошибкам первого рода относят те, при которых отвергается правильная гипотеза. К ошибкам второго рода, относят те, при которых принимается неправильная гипотеза. Допустимой вероятностью ошибки первого рода является q-уровень значимости. Однако. если уменьшать q, то возрастает вероятность принятия неверной гипотезы, т. е. вероятность ошибок второго рода. Если справедлива гипотеза H1, то это считается доказанным, если справедлива гипотеза H0-то говорят, что результаты эксперимента не противоречат нулевой гипотезы. Для того чтобы считать H0 доказанной нужно или вновь повторить эксперимент или проверить гипотезу с помощью других критериев.
Похожие работы
... ошибки первого рода; 3) определить область допустимых значений и так называемую критическую область; 4) принять то или иное решение на основе сравнения фактического и критического значений критерия. Проверка статистических гипотез складывается из следующих этапов: - формулируется в виде статистической гипотезы задача исследования; - выбирается статистическая характеристика гипотезы; - ...
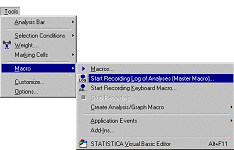
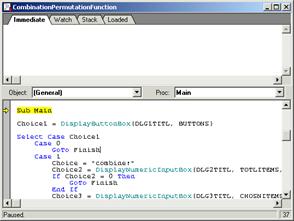
... широкие возможности по созданию макросов. В ходе написания данной курсовой работы был создан макрос на языке SVB для проверки гипотезы о нормальности остатков регрессии. Необходимость разработки данного приложения связана с особенностями осуществления регрессионного анализа в пакете STATISTICA. Написанный модуль был использован при эконометрическом моделировании вторичного рынка жилья в г. ...
... 362 406 342 441 391 390 432 374 280 395 Путем статической обработки результатов измерений выполнить следующие пункты задания: Задание 1. Первичная статистическая обработка информации. 1. Построить вариационный статистический ряд. 2. Определить размах колебаний вариант. 3. Построить эмпирическую функцию распределения. 4. Выбрать число и длины разрядов (интервалов) и ...
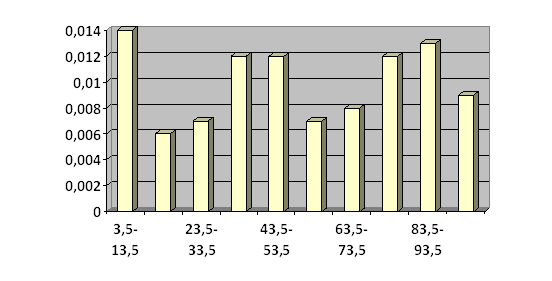
... После того, как найдены значения функции плотности для каждого разряда, нанесем их прямо на гистограмму, получая тем самым кривую функции плотности 7 Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона В качестве меры расхождения между статистическим и гипотетическим (теоретическим) распределениями возьмем критерий Пирсона К = ч2. Пирсон доказал, что ...
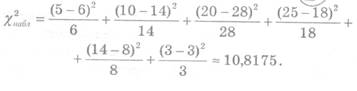

0 комментариев