Деятельностная теория учения

1.4.1 Деятельностная теория учения

Основы этой теории, имеющей свое начало еще в трудах А. Дистервега, в XX веке были разработаны отечественными учеными Л.С. Выготским, С.Л. Рубинштейном, А.Н. Леонтьевым, П.Я. Гальпериным, Д.Б. Элькониным, В.В. Давыдовым и др.

Деятельностная теория (подход) опирается на представление о структуре целостной деятельности (потребности-мотивы-цели-условия-действия) и объясняет процесс активно-исследовательского усвоения знаний и умений посредством мотивированного и целенаправленного решения задача (проблем). Решение задачи состоит в поиске действия, с помощью которого можно так преобразовать ее условие, чтобы достигнуть результата.

Разработчики отдельных направлений деятельностной теории ставили акценты на различные компоненты целостной структуры деятельности, (теория содержательного обобщения Д.Б.Эльконина – В.В.Давыдова, теория поэтапного формирования умственных действий П.Я.Гальперина – Н.Ф.Талызиной, теория социального научения А.Бандуры – Е.Маккоби, когнитивная теория учения Д.Бруннера – С.Пайперта).

 

1.4.2 Теория содержательного обобщения В.В. Давыдова – Д.Б.Эльконина

В основу этой концепции обучения положена гипотеза о ведущей роли теоретического знания и, в частности, содержательного обобщения в формировании интеллекта. Учебная деятельность ребенка представляется как познавательная, построенная по теоретико-дедуктивному (в отличие от эмпирически-индуктивного) типу. Реализация ее достигается формированием у учащихся теоретического мышления путем специального построения учебного предмета и особой организации познавательной деятельности.

Учебный предмет не просто излагает систему знаний, а особым образом (построение его содержания) организует освоение ребенком содержательных обобщений – генетически исходных, теоретически существенных свойств и отношений объектов, условий их происхождения и преобразования. Понятие "субъект познания" выступает в этой концепции как способность ученика овладеть научными понятиями, организованными по теоретическому типу, воспроизвести в собственной деятельности логику научного познания, осуществить восхождение от абстрактного к конкретному. Иными словами, учение выступает как деятельность по воспроизводству содержания, пути, метода научного (теоретического) познания.

Введение нового понятия в процессе обучения проходит четыре стадии.

1) Знакомство с предлагаемой учителем ситуацией математической, лингвистической или иной задачи, ориентирование в ней.

2) Овладение образцом такого преобразования материала, которое выявляет наиболее существенные отношения, служащие основой решения задачи данного вида.

3) Фиксация выявленных отношений в форме той или иной (предметной или знаковой) модели.

4) Выявление тех свойств выделенного отношения, благодаря которым можно вывести условия и способы решения исходной частной задачи.

 

1.4.3 Теория поэтапного формирования умственных действий

В отечественной психологии разработана одна из интереснейших теорий усвоения– теория поэтапного формирования умственных действий (Л.С.Выготский, П.Я.Гальперин, Н.Ф.Талызина). В ее основе лежит идея о принципиальной общности внутренней и внешней деятельности человека. Согласно этой идее, умственное развитие, как и усвоение знаний, навыков, умений, происходит путем интериоризаиии, т.е. поэтапным переходом “материальной” (внешней) деятельности во внутренний умственный план. В результате такого перехода внешние действия с внешними предметами преобразуются в умственные – интериоризируются. При этом они подвергаются обобщению, вербализуются, сокращаются, становятся готовыми к дальнейшему внутреннему развитию, которое может превышать возможности внешней деятельности.

Последовательность обучения на основе теории поэтапного формирования умственных действий слагается из этапов.

1. Предварительное знакомство с действием, создание ООД. Происходит предварительное ознакомление с действием, т.е. построение в сознании обучаемого ориентировочной основы действия (обозначим это как ООД).

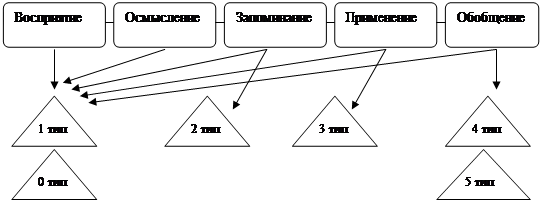
ООД – текстуально или графически оформленная модель изучаемого действия, система условий правильного его выполнения. Различают несколько типов ООД: полный, неполный, инвариантный и др.

2. Материальное (материализованное) действие. Обучаемые выполняют материальное (материализованное) действие в соответствии с учебным заданием во внешней материальной, развернутой форме. Они получают и работают с информацией в виде различных материальных объектов: реальных предметов или их моделей, схем, макетов, чертежей и т.д., сверяя свои действия с ООД (инструкцией).

3. Этап внешней речи. После выполнения нескольких однотипных действий необходимость обращаться к инструкции отпадает и функцию ориентировочной основы выполняет внешняя речь. Обучаемые проговаривают вслух то действие, ту операцию, которую в данный момент осваивают. В их сознании происходит обобщение, сокращение учебной информации, а выполняемое действие начинает автоматизироваться.

4. Этап внутренней речи. Обучаемые проговаривают выполняемое действие, операцию про себя, при этом проговариваемый текст необязательно должен быть (полным, обучаемые могут проговаривать только наиболее сложные, значимые элементы действия, что способствует его дальнейшему мысленному свертыванию и обобщению.

5. Этап автоматизированного действия. Обучаемые автоматически выполняют отрабатываемое действие, даже мысленно не контролируя себя, правильно ли оно выполняется. Это свидетельствует о том, что действие интерио-ризировалось, перешло во внутренний план и необходимость во внешней опоре отпала.

2 МОДУЛЬНОЕ ОБУЧЕНИЕ 2.1 Общие сведения о технологии модульного обучения

В последнее десятилетие одной из самых распространённых мировых тенденций в образовании стала реализация как личностно ориентированных, так и информационных технологий.

К личностно-ориентированным технологиям, то есть тем технологиям, которые используются в условиях обычного класса любого типа школ, например, КСО, обучение в парах, обучение в сотрудничестве, метод проектов, разноуровневое обучение относится и технология модульного обучения.

Модульная педагогическая технология конструируется на основе ряда целей. Важнейшая из них – создание комфортного темпа работы для каждого ученика.

Каждый ученик получает шанс определить свои возможности в учении и приспособиться к тем уровням изучения материала, которые предложены учителем.

Самым главным отличием этой технологии является применение принципа планирования совместной деятельности учителя и ученика.

Описание процесс планирования:

Первое – определяются цели для учащихся, то есть устанавливается, кто хочет знать не более государственного стандарта, а кто готов заниматься больше, поскольку планирует поступать в ВУЗ или просто хочет высокий балл. После того, как учащиеся определились с целями:

Второй момент – учитель выстраивает своё целеполагание, определяя содержание и объём педагогической помощи учащимся.

Третий момент – исходя из целей проектируется итоговая диагностика, то есть с учётом уровневой дифференциации создаётся диагностическая карта, она позволяет учащимся осознанно определять тот минимум знаний, который необходим для получения того или иного балла.

Четвёртый момент – на основании целеполагания и планируемой итоговой диагностики отбираются предметное содержание в смысле задания из учебника и из дидактических материалов.

Пятый момент – на основании отобранного содержания выстраивается логика изучения темы, то есть поурочное планирование, определяется время и место промежуточной и итоговой диагностик (то есть изучения запросов учеников) и учебной коррекции.

Шестой момент – для каждого урока определяются цели учащихся и приёмы обратной связи; создаются опорные конспекты для учащихся и задания к уроку.

Модульная педагогическая технология помогает осуществлять индивидуальный подход к учащимся, включать каждого в осознанную учебную деятельность, мотивировать её, формировать навыки самообучения и самоорганизации, обеспечивая тем самым постепенный переход от пассивного ученика кк сотрудничеству ученика и учителя.

2.2 Чем хороши модульные уроки?

1. Новая ступень к развитию самостоятельности учащихся.

2. Учит детей усваивать предложенный способ обработки новой учебной информации.

3. Получать результат соответствующий эталону.

4. У учащихся формируются умения планировать свою деятельность, более осознанно ориентироваться в учебном материале.

5. Совершенствуют навыки самостоятельной работы не только на этапе усвоения новых знаний, но и на этапе применения, обобщения и систематизации.

6. Эффективны не только как средство формирования знаний, умений и навыков, но и как средство обучения учащихся способам умственных действий и диагностики уровня овладения ими.

7. Позволяет осуществить индивидуальный подход с учётом субъективного опыта ученика, уровня его обученности и обучаемости.

Некоторые сведения об истории модульного обучения содержатся в журнале «Советская педагогика», № 1, 1990.

Адреса передового педагогического опыта по модульной технологии:

1) г. Гомель, СШ № 56.

2) Гомельский район, Урицкая СШ.

3) г. Мозырь, СШ № 12.

4) г. Светлогорск, СШ № 4, 9.

2.3 Использование элементов модульной технологии и рейтинговой оценки знаний при дифференциации в обучении математике

В обучении математике дифференциация имеет особое значение, что объясняется спецификой этого предмета. Математика объективно является одной из самых сложных школьных дисциплин и вызывает субъективные трудности у многих школьников. В то же время имеется большое число учащихся с явно выраженными способностями к этому предмету. Разрыв в возможностях восприятия курса учащимися, находящимися на двух «полюсах», весьма велик.

Как успех учебного процесса в целом, успех дифференцированногоподхода в обучении существенно зависит от познавательной активности учащихся, от того, насколько они будут заинтересованы в своей деятельности. Ясное знание конкретных целей при условии их посильности, возможность выполнить требования учителя активизирует познавательные способности школьников, причём наразных уровнях. Если цели известны и посильны ученику, а их достижение поощряется, то для подростка нет ничего естественнее, как стремиться к их выполнению. Уровень, на котором ведётся преподавание, не надо отождествлять с обязательным уровнем усвоения материала. Уровень преподавания должен быть в целом существенно выше, иначе и уровень обязательной подготовки не будет достигнут, а учащиеся, потенциально способные усвоить больше, не будут двигаться дальше. Каждый ученик должен пройти через полноценный учебный процесс. Так, он должен в полном объёме услышать предлагаемый материал со всеми доказательствами и обоснованиями, ознакомиться с образцами рассуждений, на каких-то этапах участвовать в решении более сложных задач.

Дифференциация осуществляется не за счёт того, что одним ученикам дают меньше, а другим больше, а в силу того, что предлагая ученикам одинаковый объём материала, устанавливают различные уровни требования к его усваению. Для эффективности дифференцированного обучения можно использовать элементы модульной технологии. Действительно, при модульном обучении каждый ученик включается в активную учебно-познавательную деятельность. Здесь идёт индивидуализация контроля, самоконтроля, коррекции, консультирования, степени самостоятельности. Важно, что ученик имеет возможность в большей степени самореализаваться и это способствует мотивации учения. У школьников формируются такие качества как самостоятельность и коллективизм. Принципиально меняется и положение учителя в учебном процессе. Прежде всего, изменяется его роль. Задача учителя – обязательно мотивировать учащихся, осуществлят управление их учебно-познавательной деятельностью через модуль и непосредственно консультировать школьников. Учитель как бы беседует с учеником, активизирует его на рассуждения, поиск, догадку, подбадривает, ориентирует на успех.

Преимущества использования модульного обучения в том, что оно интегрирует в себе всё то прогрессивное, что накоплено в теории и практике.

Из программированного обучения заимствует идея активности ученика в процессе его четких действий в определённой логике, постоянное подкрепление своих действий на основе самоконтроля, индивидуализированный темп учебно– познавательной деятельности.

Из теории поэтапного формирования умственных действий используется самая её суть – ориентировочная основа деятельности.

Кибернетический подход обогатил модульное обучение идеей гибкого управления деятельностью учащихся, переходящего в самоуправление.

Из психологии используется также рефлексивный подход.

Тему можно разделить на восемь модулей, не являющихся 8 уроками. Модуль может содержать несколько уроков.

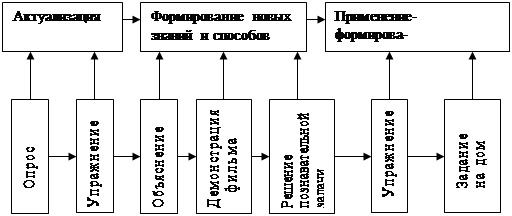
Шесть первых модулей, в основном, построены по схеме:

ПОСТАНОВКА ПРОБЛЕМЫ

При постановке проблемы учащимся предлагается свободная таблица тех знаний (схематично), которые учащиеся приобретут на последующих уроках.

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Перед изучением нового материала проводится входной контроль знаний и умений (например, в форме диктанта с обязательной проверкой сразу после написания), чтобы иметь информацию об уровне готовности к работе. При необходимости проводится соответствующая коррекция знаний. В той части модуля, где изучается новый материал, хорошо вписывается вся система методов приёмов и форм организации учебно-познавательной деятельности учащихся: работа индивидуальная, в паре, в группе, лекционная система, беседы и т. д.

САМОСТОЯТЕЛЬНАЯ ПРАКТИКА

ученика по использованию вновь полученных знаний, сочетающихся с индивидуальной помощью со стороны учителя

При самостоятельной работе над задачей ученики используют учебник, дополнительную литературу, консультации учителя.

ВЫХОД НА КОНТРОЛЬ

Завершающий этап каждого модуля – выход на контроль, который состоит из трёх уровней сложности. Все предлагаемые задания оценены определённым количеством баллов.

Учащиеся сами выбирают для себя уровень сложности и не испытывают беспокойства по поводу получения неудовлетворительной оценки, т. к. каждый из них получит не отметки, а количество баллов.

Предпоследний модуль можно назвать уроком –

Консультацией.

Урок – консультация.

Класс разбит на пять групп. Каждая группа получает задание (7 вопросов).

Время подготовки 7-8 минут. После подготовки каждая группа отвечает на вопросы, предлагаемые на кодоскопе, затем сдаёт свои вопросы экспертам (ответы должен написать каждый). После ответа одной группы остальные высказывают свои дополнения, возражения и т. д.

В этом модуле можно рассматривать решения задач нестандартными методами. Задания предлагаются каждой группе. Время подготовки 10 минут. Оценивается в баллах. Каждая группа записывает решение на кодоскопе. Проходит обсуждение. Завершение модуля – «Ярмарка задач», где каждый ученик решает индивидуальные задания. Задачи, например, можно выдать в конверте каждой группе. Они разной степени сложности на «3», «4», «5» баллов.

Последний модуль – это контрольная работа,

задания которой содержат обязательные задачи повышенной сложности. За неё учащиеся получают оценку в баллах.

По окончанию изучения темы, ученик имеет три оценки, которые видны из таблицы:

«Рейтинг ученика»

Фамилия ученика
Модули (1-6)
Баллы за промежуточный контроль		Общее количество баллов	Оценка
Урок – консультация
Баллы за задания на уроке	Общее количество баллов		Оценка
Контрольная работа
Баллы за задания		Общее количество баллов	Оценка
Зачёт

Последняя графа отведена для тех, кто желает повысить свою оценку за первые шесть модулей. Рейтинговая система оценки увеличивает желание ученика получить большее количество баллов, а, следовательно, школьник старается выбирать и решить более трудные задачи и получить более глубокие знания.

Введение модулей в учебный процесс надо осуществлять постепенно. Можно сочетать традиционную систему обучения с модульной.

Элементы модульной системы применимы и в младших классах, а консультацию – зачёт можно провести следующим образом:

Учащимся заранее выдаются вопросы для самоконтроля. Затем 6 учеников, получивших лучшие оценки за самостоятельные работы, отвечают у доски.

Это будущие консультанты. За ответы учитель сам ставит оценку. Но остальные учащиеся, которые в дальнейшем будут отвечать консультантам, следят за его ответом и имеют право обсуждать и оценивать. Когда проходит работа в группе, ребята имеют право задавать вопросы спрашивающему, консультироваться у учителя, но за каждый вопрос у ученика снимается по одному баллу (штрафные очки). После этого можно проводить контрольную работу.

Эффективным методом при дифференцированном обучении является работа в группе. За 10 дней до семинара учащимся сообщаются теоретические вопросы, по которым будет вестись опрос, и домашнее задание. Домашнее задание лучше подобрать творческого характера, так, чтобы учащиеся или сами сочинили какую-либо задачу или заглянули в дополнительную литературу по математике. Иногда можно задавать задание для всех 4 групп, на которые разбит класс.

Например, 4 каких-нибудь примера с «изюминкой» или 4 интересные задачи. Но спрашивать не все 4 задачи, а только по одной. Представители от группы тянут жребий, кому отвечать 1, 2, 3, 4. Первая группа выбирает ту из задач, какая ей больше понравилась и т. д. Класс разбит на четыре группы, равные по силе. Это нужно для того, чтобы ученики при решении задач помогали друг другу и для того, чтобы на уроке присутствовал дух соревнования.

Урок начинается с исторической справки, подготовленной одним учеником из учеников. Затем идёт опрос теории. Задаются вопросы, оцененные в 1, 2, 3, 4, 5 баллов. Учащиеся отвечают на вопросы, тем самым зарабатывая очки для группы. Если ученик отвечает неправильно, то баллы, наоборот, снимаются со счёта группы. Домашнее задание тоже оценивается определённым количеством баллов. При проверке могут быть различные варианты оценок. Заключительным этапом может быть «ярмарка задач». Здесь учитывается различный уровень подготовленности учащихся.

Самое главное – вызывать у учеников интерес к предмету и пробудить желание заниматься математикой в дальнейшем.

Технология модульного обучения - одна из технологий, которая, по сути являясь личностно-ориентированной, позволяет одновременно оптимизировать учебный процесс, обеспечить его целостность в реализации целей обучения, развития познавательной и личностной сферы учащихся; совместить жесткое управление познавательной деятельностью ученика с широкими возможностями для самоуправления.

Важным достоинством данной технологии является и ее интеграционное качество, ибо модуль, как целостное единство содержания и технологии его изучения, реализуется через комплекс технологий, интегрированных в модуль: проблемной, алгоритмической, программированной, поэтапного формирования умственных действий, "полного усвоения", КСО и т.д.

Эффективность технологии модульного обучения не вызывает сомнений, так как она апробирована мировым опытом (Великобритании, Голландии, США и др.) и становится все более популярной в нашей стране. Но большим препятствием к ее распространению является отсутствие дидактического обеспечения этой технологии.

Творческими группами учителей Ростова и Ростовской области под руководством доцента кафедры педагогики ИПКиПРО, кандидата педагогических наук Гульчевской В.Г. уже разработаны в результате экспериментального поиска и внедрены в учебный процесс модульные пособия для индивидуальной работы учащихся по математике (5, 8, 9 классы), по химии (10 класс полностью), некоторые темы по биологии и физике. В стадии разработки находятся пособия по другим разделам предметов естественно-научного цикла, а также по другим предметам.

Каковы возможности технологии модульного обучения в реализации существенных признаков личностно-ориентированного обучения?

Прежде всего в ней заложен принцип, который классик гуманистической психологии К. Роджерс считает основным: ученик с помощью модульной программы включен в активный, самостоятельный процесс учения, а учитель в этом процессе его сопровождает, помогая освоить приемы учения и самоуправления. При этом учитель, освобожденный от сугубо преподавательской и жесткой управленческой нагрузки, получает, наконец, реальную возможность осуществлять индивидуальный, личностный подход к каждому ученику, организовывать взаимодействие и взаимопомощь учащихся.

Благодаря открытости методической системы учителя, заложенной в модуле, добровольности текущего и гласности итогового контроля, возможности свободно осуществлять самоконтроль и выбирать уровень усвоения, отсутствию жесткой регламентации темпа изучения учебного материала, выполняется гуманистический принцип направленности на ребенка. Таким образом создаются благоприятные морально-психологические условия, в которых ребенок ощущает себя свободным, защищенным, уверенным в своих силах.

Осознание учащимися личностной значимости изучаемого и потребности в достижении определенных учебных результатов мотивируется четким описанием комплексной качественной цели, которой может ученик достичь по завершении модуля, критериев уровней усвоения и методической обеспеченностью в их достижении каждым учеником, реальный же результат всецело зависит от самого ученика.

Статус "субъекта", как одного из важнейших показателей личностно-ориентированного обучения, обеспечивается модульной технологией естественным образом, а не по разрешению извне. Он сам планирует способы, темп и место работы. Сам оценивает свои возможности и уровень притязаний. Сам принимает решение о продвижении к следующему уровню.

Потребность в самореализации удовлетворяется, во-первых, возможностью с помощью модуля учиться всегда успешно и, во-вторых, свободой выбора творческой деятельности и нестандартных заданий.

Что такое модуль и как его оформить?

Известны различные способы оформления модулей как средства организации учения школьников. Как показал наш эксперимент, технология модульного обучения осуществляется наиболее эффективно, если модульная программа представляется в виде специального учебного пособия для индивидуальной работы учащихся (по сути – самоучителя) и вручается ему для постоянного пользования на время изучения блока учебного материала, заложенного в модуль.

В структуре модульного пособия отражены требования и правила конструирования модуля:

комплексная цель, в которой заданы качественные характеристики (познавательные и личностные) результата изучения модуля;

конкретизация цели в предметных "учебных элементах", заданных стандартом образования;

программа и рекомендации технологических приемов ее изучения;

конкретизация цели в эталонах и критериях уровней усвоения, в заданиях итогового контроля;

эталоны решений для организации самоконтроля и взаимоконтроля.

Основные идеи, принципы и правила реализации модульной технологии

Модульная технология представляет собой обобщенную, универсальную систему, своего рода метатехнологию, которая являясь как бы канвой, каркасом сооружения, предназначенного для реализации целей индивидуализации, органично и оптимально интегрирует в себя любые другие технологии, необходимые для достижения конкретных образовательных и развивающих целей.

Это такая технология, которая реализует на практике следующие идеи, принципы и правила:

крупноблочная организация учебного материала вместе с рекомендациями и заданиями по его изучению;

преимущественно самостоятельная проработка учащимися учебного материала;

управление учением школьников посредством программы (последовательности заданий и этапов учебной работы) и алгоритмов познавательной деятельности (т.е. посредством учебно-методического комплекта, называемого модулем);

открытость методической системы учителя (программа изучения материала и планирование работы на уроке сообщается учащимся заранее);

возможность выбора учащимися уровня усвоения, форм, места и темпа изучения материала;

добровольность домашней работы;

создание условий для успешной познавательной деятельности для каждого ученика;

перспективное нацеливание учащихся на критерии и содержание контроля;

демонстрация безграничного доверия к ученику, уверенности в его возможностях;

свободный самоконтроль и взаимопомощь в процессе работы на уроке;

только содержательный (безотметочный) оперативный текущий контроль;

оценка результатов по итоговому контролю (а не как среднее арифметическое текущих результатов);

предоставление каждому ученику шанса улучшить свои итоговые результаты;

возможность реализовать себя в творческой деятельности;

участие учащихся в оценке эффективности учебного процесса.

3 ЭЛЕМЕНТЫ МОДУЛЬНОЙ ТЕХНОЛОГИИ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ УЧАЩИХСЯ 6-ГО КЛАССА

Общий комментарий к проводимому эксперименту

3.1 Исходные условия экспериментального внедрения элементов модульной технологии в 6-ом классе СШ № 3 г. Добруша

Экспериментальная часть.

Экспериментальную часть я разделила на 3 этапа:

Первый – диагностирующий.

Второй – контролирующий.

Третий – итоговый.

Диагностирующий этап.

Первым шагом в моём диагностическом этапе было знакомство с классом 2 года назад. Класс был “сфабрикованным”, то есть две параллели четвёртых классов посортировали. В 5 “А” зачислили лучших из лучших по всем параметрам учащихся и назвали этот класс “Гимназическим”. В 5 “Б” классе оставили всех плохоуспевающих, слабых в умственном и физическом развитии, а так же “отпетых мошенников”. Волей случая мне доверили не только вести математику в обоих классах, но и дали классное руководство как раз таки в 5“Б” классе. Учителя сочувственно кивали мне головой и некоторые говорили “ну держись, у тебя второй 8 “Б”!” это означало что подобное уже проводилось 3 года назад и как раз то 8 “Б” класс и был сбором “отпетых мошенников”. Никто и не стремился переубеждать ребят (а в подобных классах преобладающее количество мальчишек ) в том, что они не “отбросы”, а нормальный базовый класс. В результате они и стали такими. Они ненавидели школу, учителей и самих себя. Не удивительно что уже в 8 классе к ним учителя заходили на урок с опаской. Это конечно было моё личное мнение. Я считала, что если сейчас же ребят правильно настроить, то всё получиться великолепно. В.Г. Ермаков на лекциях утверждал, что нет плохих детей есть плохие учителя. Он приводил много примеров, подтверждающих это. Я так же частично ознакомилась с III-х томником В.Г. Ермакова “развивающее обучение и функции текущего контроля”. Где очевидно прослеживалась интересная суть “сделай, создай интерес на уроке математики и даже самый отстающий захочет и станет учиться”.

Учитывая, что у меня в руках был 5 “Б” (то есть ещё Малыши), я уже заранее решила воспользоваться советами В. Г. Ермакова и планировать 1-е уроки сразу стала в форме игры… Но вернемся к началу.

Первый учебный день, первый классный час – знакомство с детьми. Я предложила учащимся знакомство следующим образом: Вначале представилась я, затем по очереди встает каждый из вас, представляется, говорит немного о себе и о своем отношении к школе и математике в целом. В тот день меня очень удивила их откровенность. Почти каждый говорил о том, что школу не любит, а математику так себе. А одна девочка встала и четко, словно заученными фразами выпалила: «Я, Бондаренко Янина, люблю смотреть телевизор, кататься на велосипеде, школу не люблю, математику ненавижу!» Злобно посмотрев на меня, тут же села на место. Я не стала ее ругать, напротив, сказала, что она молодец. Ведь так искренне признаться мог не каждый.

Когда я удивленно стала выяснять о причине такого отношения к школе в целом, они почти хором говорили: «А что вы хотите? Собрали нас, «дебилов», в один класс, так и получайте результат…» Моему возмущению не было предела. «Как же так, – говорила я, – неужели вы считаете себя «дебилами»? Вот лично ты? Ты считаешь себя таким, да?» – Обратилась я к одному из мальчиков. На что он ответил: «да я-то нет, но все учителя так считают, да и родители тоже …»

После утомительной беседы с классом я поняла, что мне действительно будет не легко. Из проведенного мной классного часа, следовал вывод: Мне придется работать с педагогически запущенными детьми, у которых очень сильно занижена самооценка, не верующих в свои силы и способности, сомневающимися в себе ребятами.

Вторым шагом диагностируещего этапа стало приглашение на классный час психолога школы Н.И. Сушко. Она провела с ними тестирование на самооценку и, мои худшие подозрения оправдались.

Третьим шагом диагностики являлся контрольный срез по математике. Из 15-ти присутствовавших на том уроке детей в классе, выполнили (с ошибками) все обязательные номера только два человека. Остальные не справились даже с этим. Я убедилась в том, что математические знания ребят гораздо ниже среднего. На следующем уроке математики прослеживался явный не интерес к предмету. И тут я решила пора начинать, как говорил В. Г. Ермаков, «подвинчивать расшатанные гаечки, винтики». Конечно же это занимало уйму времени у меня дома, но цель оправдывала средства. Мне предстояло не только развить интерес у класса к математике, но и изменить их внутренний мир в целом…

Каждую до боли скучную обязательную задачу я переделывала в сказочную или шуточную.(см. Приложение 1). И тут же видела результаты. Первая же задача у учащихся вызвала интерес. Видеть их блестящие от азарта глазки было для меня наградой. Но тут новые препятствия я вдруг с ужасом поняла, что большинство из них просто-напросто не знают таблицу умножения. Пришлось вернуться и, как учил В.Г. Ермаков, потоптаться на месте. Зато далее устный счет для них уже не был проблемой быстрота решения простейших задач, страх и неуверенность постепенно рассеивались. Более того, каждый день я старалась психологически воздействовать на них, убеждая и показывая ребятам, что они молодцы, что они обычные детки, что у них не класс «отбросов», а просто базовый класс, что 5 «А» это не лучшие из лучших, а просто сильнейшие, которые будут изучать все предметы на повышенном уровне. Учитывая то, что я их не обманывала, им не составляло большого труда убеждаться в правдоподобности моих утверждений.

Наряду с этим я сочла нужным коррекционную работу с родителями. Проводя родительское собрание, я пришла к ужасающему выводу, что большинство из родителей также считают ныне 5 «Б» класс классом «дебилов». Мне пришлось ругаться на них за такой настрой и стыдить их в том, что они такого мнения о своих детях. Причем каждый из них лично своего ребенка считал нормальным, но вот, мол, попал же по случайности к «отбросам» следовательно и он скоро станет таким…Требовалось огромных усилий, чтобы переубедить их. Я даже прибегала к помощи психолога, чтобы заставить родителей поверить в своих детей. Что ж это, говорю, такое будет? Если в школе на детей будут говорить «вы отбросы», дома – «вы дебилы», на улице – «вы отсталые» и т. д.? Да в конечном итоге они и станут «дебилами», «отбросами» и т. д. А давайте наоборот. Мы в школе, а вы дома всячески поддерживать ребят. Ведь они на самом деле обыкновенный базовый класс. Родители с трудом, но согласились с моим мнением. Трудность была еще в том, что родители были все преимущественно гораздо старше меня. Воспринимать меня, как учителя, классного руководителя (учитывая, что до этого я была просто сторож) никто не хотел.

В середине учебного года мне надлежало провести открытый урок в школе. Я, к величайшему удивлению многих учителей, решила давать открытый урок, не в гимназическом 5 «А» классе, а в своем родном 5 «Б». Некоторые из учителей так и говорили: «Ты что, решила опозориться? Почему не в гимназическом классе – там же есть с кем работать не то, что в 5 «Б»? Я просто отвечала: «посмотрим». Ну и как следует предположить, ожидая моего провала, на урок ко мне пришло много желающих. Я решила сделать открытый урок-соревнование. Поделив на равные по силам команды таким образом (см. Приложение 2). Предварительно расставив удобным образом парты, команды заняли свои места. Урок начался. Из числа прибывших на урок гостей выбрали жюри, выделив их стол табличкой «господа судьи». Разминка – устный счет. Далее хитрые и интересные задачки, задачки – шутки, ребусы. Тайные задания в конвертах (абсолютно одинаковые, но ведь команды об этом не знали). Следом задания на скорость соображения, т. е. звучит один вопрос для всех, кто первый поднял руку, тот и отвечает. Но если ответ не верен, то право спокойного обсуждения и выдачу ответа получает другая команда.

На всякий случай у меня было кое-что припасено. Если не будет хватать заданий, т. е. дети вдруг справятся со всеми заданиями, и останется время, предложу задачу из книги [**Ерм 3-х, с. **] трехтомника В.Г. Ермакова «Развивающее обучение и функции текущего контроля» про гномиков. Эту задачу В.Г. Ермаков как-то придумал сам, экспериментируя во 2 классе.

Как я и предполагала задания моими ребятками «счелкались», как семечки. Разыгралось настоящее сражение 2-х команд. И еще за 10 мин. до конца урока у меня исчерпались все боевые запасы. Конечно же можно было подвести итог и оставшееся время потратить на поздравление и выводы, но уж очень мне эта часть не нравилась. Узнав от судей, что счет пока равный, предложила последний конкурс: задача от В.Г. Ермакова на закусочку. И пошло: споры, возражения, рассуждения, ответы. Но ответы были не верными. Повторение задачи, еще раз и еще раз. Снова споры, рассуждения. И вдруг одна из присутствующих учительниц, не выдерживая, вскрикивает: «Как нет? – У меня то же самое получилось!» Теперь начались споры, возражения и бурные обсуждения у присутствующих учителей. Некоторые с повышенным голосом пытались доказать свою точку зрения. Зрелище было бесподобное. Затем, шаг за шагом читая и решая эту задачу у доски, все весело пришли к одному единственно верному решению. И на обсуждении моего урока я смело говорила, что основная цель моего урока была создание сопернического духа и развитие интереса к предмету. Я считала, что именно этого я и добилась. Тут же следовало ехидное замечание: «где ты выкопала такую задачу, она не для 5 классов, она сложней?» На что я с гордостью открыла одну из книг В.Г. Ермакова и показала, что Владимир Григорьевич это проделывал успешно во 2-м классе. Мои ребятки оказались способными. У них появился интерес к изучению математики. Я радовалась еще и тому, что в душе они уже не считали себя «дебилами». В конце 5-го класса на них мало еще кто обращал внимание и результаты не сильно еще отличались от первоначальных, но боевой дух, мативация к учению и вера в себя прослеживалась уже явно.

Летние каникулы пролетели мгновенно и «мы» уже 6 «Б». Если на начало 5-го класса у них знания по математике были приблизительно равные: чуть выше, чуть ниже 3-х баллов (по пяти-бальной). То в начале 6-го уже видны были явные отличия. А здесь еще непонятная и вносящая сметение и страх 10-ти бальная система оценки знаний.(см. Приложение 3)

Скажем так, если Додыркин, Руев, Мохорев, Жилина и др. уже решали свободно большинство заданий, то Серогодский, Шабалин, Шабловская и др. с трудом считали обычные примеры. Например, Шабалин Александр однажды на дополнительный вопрос: «чему равно а квадрат? – напиши на доске ». Он, немного подождав подсказки, нарисовал вначале букву «А», затем вокруг нее изобразил квадрат.

Снова наряду с учебой, мне приходилось вносить воспитательный характер во временные рамки уроков. Где я старалась показать, что математика это наука, которую следует изучать шаг за шагом, ступенька за ступенькой. Иначе если не будет фундамента, то и наросченная сверху башня рухнет. Приводила абсурдные примеры (см. Приложение 4). Именно в это время я и пришла к выводу, что в сложившихся обстоятельствах мне просто необходимо использовать элементы модульной технологии и дифференцированный подход. Я знала, что введение модулей в учебный процесс надо осуществлять постепенно, что можно сочетать традиционную систему обучения с модульной.

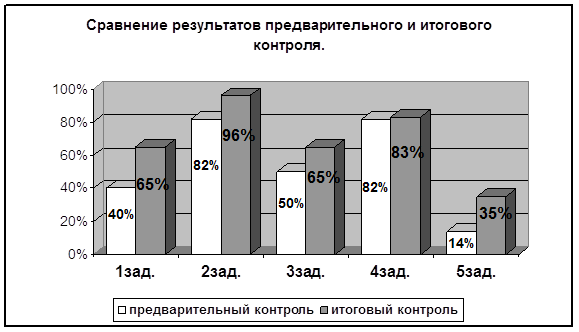
  3.2 Контролирующий этап.

Начало было более чем плавным. Я подбирала задания на конец урока при закреплении материала по уровням. Например: (см. Приложение 5). Наряду с введением модулей, новые темы, скучные задачи я старалась переделывать на лад сказки или веселой истории яко бы произошедшей у нас в классе.

Следующим нелегальным шагом моей деятельности – стали субботы. Дело в том, что субботы теперь в школах отведены для воспитательной работы, а я на свой страх и риск предложила желающим позаниматься дополнительно без оценок. В субботу минут 40-45 до мероприятия порешаем, если хотите более сложные и ли те математические задания, которые у вас вызывают страх. И в первую же субботу, вооружившись несколькими математическими заданиями, я захожу в класс… Помня беседу в начале 5-го класса (там почти все математику не любили), я была просто шокирована. Пришли все… Весь класс собирался заниматься дополнительно. Отныне каждую субботу мы стали заниматься дополнительно математикой. При чем решали исключительно то, что вызывало затруднения. Разбирали все то, что было не очень понятным и набивали руки подобными примерами.

Ребята смело задавали вопросы и стремились разобраться в самом сложном для них. Теперь у них уровень знаний очень отличался от их же самих прежних. Но и появился еще больший разбег знаний друг между другом.

Для того чтобы был новый материал понятен всем (и более сильным, и более слабым), мне приходилось объяснять нововведения переделывая их на самый простой элементарный лад. А при работе на закреплении подбирать задания приходилось каждому индивидуально. Или, разбив класс на группы, с более слабыми заниматься обычным путем, а более сильным давать задания по карточкам. Карточки составляла из трех уровней. Ребята могли делать выбор сами (интересно то, что на первых порах детки боялись брать высокий уровень и начинали с самого низкого).

Накопляемость оценок была очень велика, т. к. почти каждый ученик почти на каждом уроке получал оценочку. Используя элементы модульной технологии, однажды в качестве домашнего задания ребята получили строгие указания к изучению нового материала самостоятельно… Результат был плачевный – урок не пошел. Но отрицательный результат – тоже результат. Я поняла, что еще рано. Ребята еще не готовы. Или я где-то сделала ошибку, или я слишком многого хочу от них.

Я вернулась к обычному проведению уроков, но сохраняя те новшества, радовали меня успехами.

Ближе к концу 3 четверти начались чудеса. Однажды, придя в класс, я начала объяснение нового материала. Вдруг замечаю, что Токорев Денис не конспектирует, а что-то бубнит себе под нос и слегка размахивает руками. На замечания он не реагировал, продолжал в своем духе. Оказалось, этот мальчик дома составил конспект будущего урока и сверял свои записи в тетради с записями на доске. Данное неожиданное и по существу, и по форме проявление самостоятельной активности учащегося оказалось и весьма результативным. Тщательная проверка реферата, подготовленного Денисом Токаревым, показала практически полное отсутствие ошибок и неточностей, – за исключением отдельных грамматических погрешностей.

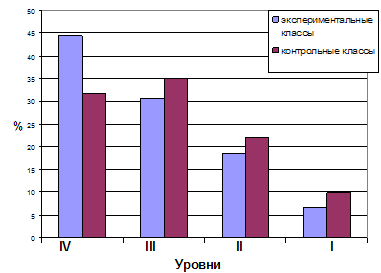
На классном часу ребятам 6 «Б» класса предложили заполнить анкету анонимно (т. е. они отвечали «да» следовательно «+», «нет» следовательно «-»). Указывать фамилию имя отчество было не нужно .

По результатам анкеты можно было судить, что всему классу нравился предмет математика и школа для них стала более привлекательной.

Заключение

Благодаря открытости методической системы учителя, заложенной в модуле, добровольности текущего и гласности итогового контроля, возможности свободно осуществлять самоконтроль и выбирать уровень усвоения, отсутствию жесткой регламентации темпа изучения учебного материала, выполняется гуманистический принцип направленности на ребенка. Таким образом создаются благоприятные морально-психологические условия, в которых ребенок ощущает себя свободным, защищенным, уверенным в своих силах.

Осознание учащимися личностной значимости изучаемого и потребности в достижении определенных учебных результатов мотивируется четким описанием комплексной качественной цели, которой может ученик достичь по завершении модуля, критериев уровней усвоения и методической обеспеченностью в их достижении каждым учеником, реальный же результат всецело зависит от самого ученика.

Статус "субъекта", как одного из важнейших показателей личностно-ориентированного обучения, обеспечивается модульной технологией естественным образом, а не по разрешению извне. Он сам планирует способы, темп и место работы. Сам оценивает свои возможности и уровень притязаний. Сам принимает решение о продвижении к следующему уровню.

Потребность в самореализации удовлетворяется, во-первых, возможностью с помощью модуля учиться всегда успешно и, во-вторых, свободой выбора творческой деятельности и нестандартных заданий.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Педагогика: педагогические теории, системы, технологии: Учеб. для студ. высш. и сред. учеб. заведений / С.А.Смирнов, И.Б.Котова, Е.Н.Шиянов и др.; Под ред. С.А.Смирнова. – 3-е изд. – М.: Издательский центр "Академия", 1999. – 512 с.

Селевко Г.К. Современные образовательные технологии: Учебное пособие. – М.: Народное образование, 1998. – 256 с.

Селевко Г.К. Опыт системного исследования педагогических технологий (продолжение) // Школьные технологии. 1997, № 1. – С. 11-35.

Селевко Г.К. Педагогические технологии на основе дидактического усовершенствования и реконструирования материала // Школьные технологии. 1997, № 2. – С. 29-40.

Селевко Г.К. Технологии развивающего обучения // Школьные технологии. 1997, № 4. – С. 22-46.

Стефановская Т.А. Педагогика: наука и искусство. Курс лекций. Учебное пособие для студентов, преподавателей, аспирантов. – М.: Совершенство, 1998. – 368 с.

Гальперин П.Я. Методы обучения и умственное развитие ребенка. – М.: Изд-во МГУ, 1985. – 45 с.

Ильенков Э.В. Об идолах и идеалах. – М: Политиздат, 1968. – 319 с.
(Раздел "Школа должна учить мыслить")

Варенова Л.И., Куклин В.Ж., Наводнов В.Г. Рейтинговая Интенсивная Технология Модульного обучения. – 1993. – 67 с.

Зачеты в системе дифференцированного обучения математике / Л.О.Денищева, Л.В.Кузнецова, И.А.Лурье и др. – М.: Просвещение, 1993. – 192 с.: ил. – (Б-ка учителя математики).

Давыдов В.В. О понятии развивающего обучения // Адукацыя i выхаванне, 1995, № 12. – С. 6-20.

Давыдов В.В. Теория развивающего обучения.– М.: ИНТОР, 1996.–544 с.

Репкина Н.В. Что такое развивающее обучение? Научно-популярный очерк. – Томск: Пеленг, 1993. – 64 с.

Репкина Н.В. Система развивающего обучения в школьной практике // Вопросы психологии. – 1997. – № 3. – с. 40–51.

Ермаков В.Г. Развивающее образование и функции текущего контроля. В 3 частях. – Гомель: ГГУ им. Ф.Скорины, 2000. – 778 с.