Навигация
Определение степени значимости требований к основному материалу, их весомости
3.2 Определение степени значимости требований к основному материалу, их весомости
При определении степени значимости требований к материалам и их весомости воспользуемся общей иерархической структурой показателей качества материалов.
Для вычисления комплексных оценок качества материалов единичные показатели качества, имеющие различную размерность, переводим в безразмерные одинаковые показатели. Безразмерные показатели в виде ранговых оценок, баллов, индексов качества, показателей желательности представляем в матричной форме, а подсчет комплексных оценок производим методом средней арифметической, средней геометрической или средней гармонической.
Для этого выбираем 25 наиболее важных единичных показателей качества материалов и располагаем в таблице 3.1 в порядке убывания их значимости, при этом повторов показателей свойств не должно быть.
Сущность метода экспертной оценки (ГОСТ 2355401-79) заключается в следующем: составляется перечень n=25 свойств материала, выбранных согласно требованиям, предъявляемым к данному материалу (табл. 3.1).
Ранговую оценку проводит группа экспертов из 10 человек путем расстановки присвоенного места значимости показателя, (табл. 3.1), от наиболее значимого – ранг R = 1 (первое место), к наименее значимому – R=25 (25 место).
Если какие-либо свойства, по мнению эксперта, равнозначны, то берем суммы их рангов и делим на количество этих свойств. Полученное число рангов подставляем каждому из этих свойств. Результаты опроса в виде табл. 3.1 используем для определения значимости факторов, степени согласованности ранговых оценок и коэффициента согласия.
Далее обрабатываем результаты опроса мнения экспертов.
1. Определяем сумму рангов по каждому эксперту (по горизонтали), которая для всех экспертов должна быть одинаковой:
 , (3.1)
, (3.1)
где n – количество свойств.
2. Вычисляем сумму рангов для каждого свойства (по вертикали):
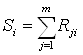 (3.2)
(3.2)
где m – число экспертов.
3. Рассчитываем среднюю сумму рангов. Для этого складываем все суммы рангов каждого свойства ![]() , и полученный результат делим на количество свойств n:
, и полученный результат делим на количество свойств n:
 , или
, или ![]() (3.3)
(3.3)
4. Находим разность между суммой рангов каждого фактора свойства ![]() и средней суммой рангов
и средней суммой рангов ![]() по каждому свойству.
по каждому свойству.
![]()
![]() (3.4)
(3.4)
5. Определяем сумму квадратов отклонений:
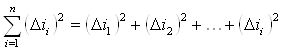 (3.5)
(3.5)
6. Если у эксперта имеются свойства с одинаковыми рангами, вычисляем сумму связанных рангов в j-м ранжировании (по горизонтали):
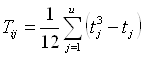 , (3.6)
, (3.6)
где u – число рангов с одинаковыми оценками j-го эксперта; t – число (одинаковых) рангов j-го эксперта.
7. Рассчитываем сумму связанных рангов всех экспертов:
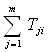 . (3.7)
. (3.7)
8. Находим согласованность экспертных оценок (коэффициент согласованности мнений экспертов) – коэффициент конкордации:
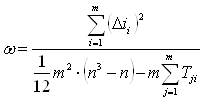 (3.8)
(3.8)
где 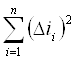 – сумма квадратов отклонений.
– сумма квадратов отклонений.
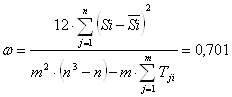
При наличии одинаковых рангов у разных показателей у одного эксперта по формуле (3.6) вычисляем значения ![]() .
.
Использовать коэффициент конкордации можно после оценки по значимости, которую находим из специальных таблиц или из известных статистических распределений. Например, величина ![]() имеет распределение
имеет распределение ![]() с числом степеней свободы f = n - 1.
с числом степеней свободы f = n - 1.
9. Рассчитаем критерий Пирсона:
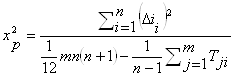
Если связанных рангов не имеется, то ![]() (10)
(10)
Гипотеза о наличии согласия экспертов может быть принята при условии, что при заданном числе степеней свободы табличные значения меньше расчетных для 5% уровня значимости.
Значения ![]() в зависимости от числа степеней свободы приведены в таблице 3.2.
в зависимости от числа степеней свободы приведены в таблице 3.2.
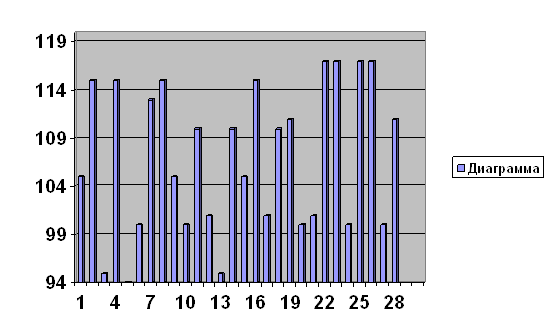
Сравнив расчетное значение ![]() с табличными данными, взятыми при достоверности 0.05 для (n-1)=25-1=24 получим x2=36.415. В связи с тем, что табличные значения критерия меньше расчетных, можно с 95%-й доверительной вероятностью сделать вывод о том, что коэффициент конкордации является значимым, т.е. оценки экспертов согласованы. Оценив согласованность мнений всех экспертов, строят диаграмму рангов, откладывая по одной оси факторы (свойства), по другой – соответствующие суммы рангов.
с табличными данными, взятыми при достоверности 0.05 для (n-1)=25-1=24 получим x2=36.415. В связи с тем, что табличные значения критерия меньше расчетных, можно с 95%-й доверительной вероятностью сделать вывод о том, что коэффициент конкордации является значимым, т.е. оценки экспертов согласованы. Оценив согласованность мнений всех экспертов, строят диаграмму рангов, откладывая по одной оси факторы (свойства), по другой – соответствующие суммы рангов.
Вывод: сравнив расчетное значение ![]() с табличными данными, взятыми при достоверности 0.05 для (n-1)=25-1=24 получим
с табличными данными, взятыми при достоверности 0.05 для (n-1)=25-1=24 получим![]() =36,415. В связи с тем, что табличные значения критерия меньше расчетных, можно с 95%-й доверительной вероятностью сделать вывод о том, что коэффициент конкордации является значимым, т.е. оценки экспертов согласованы. Оценив согласованность мнений всех экспертов, строят диаграмму рангов, откладывая по одной оси факторы (свойства), по другой – соответствующие суммы рангов.[8]
=36,415. В связи с тем, что табличные значения критерия меньше расчетных, можно с 95%-й доверительной вероятностью сделать вывод о том, что коэффициент конкордации является значимым, т.е. оценки экспертов согласованы. Оценив согласованность мнений всех экспертов, строят диаграмму рангов, откладывая по одной оси факторы (свойства), по другой – соответствующие суммы рангов.[8]
Похожие работы
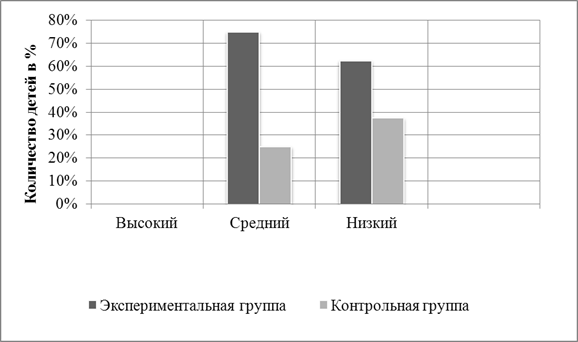
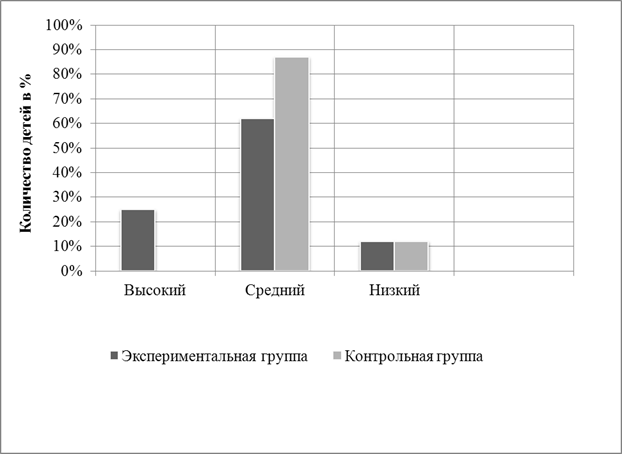
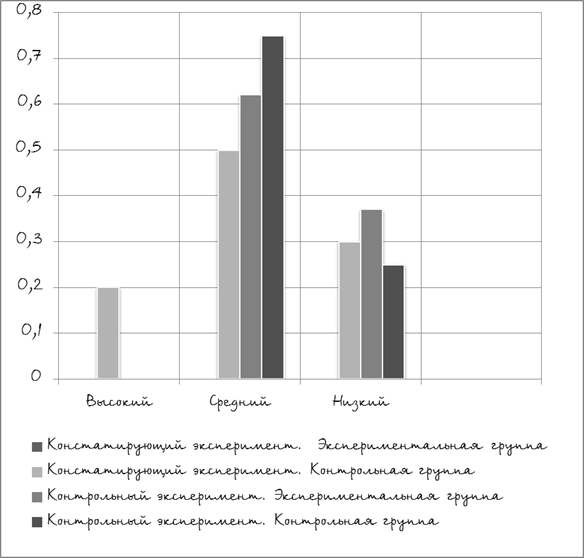
... констатирующего эксперимента был проведён формирующий эксперимент. Перед нами была поставлена задача: путём разработки и апробации системы работы воспитателя поспособствовать более эффективному процессу полоролевой социализации детей среднего дошкольного возраста. 3. Контрольные этапы эксперимента (идентичные констатирующему) выявили, что количество детей с показателями высокого уровня ...
... детьми в данном направлении не проводилась. Следовательно, комплекс ролевых игр является эффективным средством формирования ролевой игры у умственно отсталых детей старшего дошкольного возраста. Заключение Огромная роль в развитии и воспитании ребенка принадлежит игре – важнейшему виду детской деятельности. Она является эффективным средством формирования личности дошкольника, его морально- ...
... оборудования. Целью данной курсовой работы является разработка технологической последовательности по изготовлению женского комплекта с применением новейшего высокопроизводительного оборудования и усовершенствованных методов обработки. Нормативно техническая документация ГОСТы, ОСТы, применяемые для пошива изделия Одежда платьево - блузочного ассортимента общие технические условия ГОСТ 2594 ...
... школьного возраста. Работа клуба планируется с учетом индивидуальных особенностей детей, а также реальных возможностей руководителя. Рассмотрим примерный план деятельности клуба на базе Черлакского детского дома Омской области. План работы клуба «Деловые ребята» для старших школьников. 2000-2001 год. Сентябрь-Октябрь. «Формирование имений и навыков труда в домашнем хозяйстве» ...

0 комментариев