Навигация
Расчет электрических цепей синусоидального тока
7316
знаков
0
таблиц
4
изображения
КОНТРОЛЬНА РОБОТА
з дисципліни
“Електротехніка в будівництві”
Задача 1
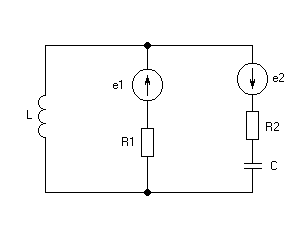
Рассчитать электрическую цепь синусоидального тока с последовательным соединением приемников.
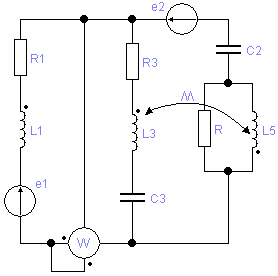
Для схемы, изображенной на рис.1, известно, что U = 110 B, R1 = 10 Oм, R2 = 10 Oм, L2 = 80 мГн, С2 = 200 мкФ, R3 = 10 Oм.
Определить ток цепи, падение напряжений на элементах цепи, активную, реактивную и полную мощность цепи, коэффициент мощности / cosj / цепи. Построить топографическую векторную диаграму.
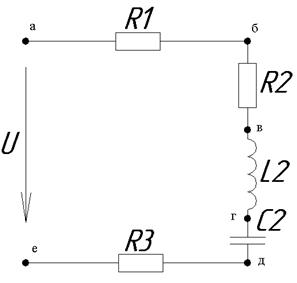
Рис. 1
Решение. Определяем реактивные сопротивления участков цепи:
Ом
Ом
Общее сопротивление цепи:
Ом
Комплексное значение тока в цепи в показательной форме:
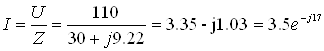А
Если начальная фаза напряжения не задана, удобнее принять ее равной нулю и расположить вектор напряжения совпадающим с вещественной осью комплексной плоскости. В этом случае мнимая составляющая комплекса напряжения также равна нулю: 
110 В.
Рассчитываем комплексные значения напряжений на элементах цепи в показательной и алгебраической формах:
В
В
В
В
В
Активную, реактивную и полную мощности цепи определяем из соотношения:
,
где 
- сопряженный комплекс тока,
Знак “ + “ перед реактивной мощностью говорит о том, что она имеет индуктивный характер.
Правильность решения проверяем, составив баланс мощностей:
Вт;
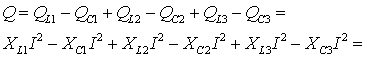113.23 вар.
Активную и реактивную мощности можно найти следующим образом:
110·3.5·cos(-170)=368.54 Вт;
110·3.5·sin(-170)=113.23 вар,
где j — угол между векторами тока и напряжения.
Проверка баланса напряжений показывает, что задача решена правильно:
В
Угол между током и напряжением определяем, сравнивая комплексы напряжений 
и тока 
:
В, 
А,
-170, 
0.956.
При построении векторной диаграммы на комплексной плоскости считаем, что потенциал точки е равен 0. Тогда из точки е, помещенной в начало координат, под углом -170 относительно вещественной оси в выбранном масштабе строим вектор UR3. Конец этого вектора будет определять потенциал точки д. Под углом -1070 к вещественной оси строим вектор UC2 определяя потенциал точки г. Из точки г под углом 730 строим вектор UL2, определяя потенциал точки в. Из точки в строим вектор напряжения UR2, определяя потенциал точки б. Из точки б строим вектор напряжения UR1, определяя потенциал точки а. Конец вектора UR1 должен определять потенциал точки а, которая должна лежать на вещественной оси, а длина отрезка еа в соответствии с выбранным масштабом должна быть равной U=110 В.
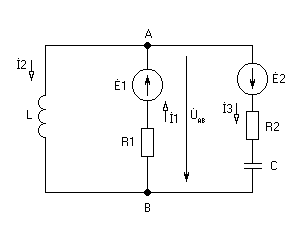
Задача 2
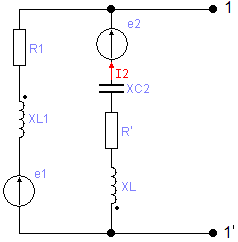
Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников, схема которой изображена на рис. 2. Дано: U = 380 B, L0 = 19 мГн, R0 = 8 Oм, L1 = 25,5 мГн, R1 = 6 Oм, R2 = 10 Oм, С2 = 396 мкФ.
Определить общий ток цепи 
и токи в ветвях 
и 
, напряжения на участках цепи, активную, реактивную и полную мощности, построить потенциальную диаграмму на комплексной плоскости.
Рис. 2
Решение. Определяем реактивные сопротивления цепи:
Ом
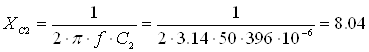Ом
Ом
Выражаем сопротивление ветвей цепи в комплексном виде:
Ом
Ом
Ом
Перевод комплексных чисел в показательную форму не обязателен, но при умножении и делении комплексных чисел показательная форма записи удобнее.
Находим эквивалентное сопротивление параллельных ветвей:
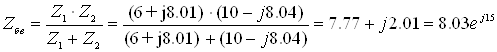Ом
Схема рассчитываемой цепи теперь имеет вид цепи с последовательным соединением приемников.
Комплексное сопротивление всей цепи:
Ом
Определим ток в неразветвленной цепи. Для этого выразим приложенное к цепи напряжение 
в комплексной форме. Так как в условии задачи начальная фаза напряжения не задана, принимаем ее равной нулю, располагая тем самым вектор напряжения с вещественной осью комплексной плоскости:
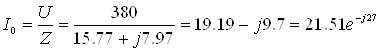А
Определяем комплексное действующее значение на разветвленном участке цепи:
В
Комплексное действующее значение на неразветвленной части цепи
В
Определяем токи в ветвях цепи:
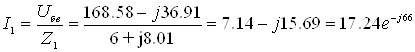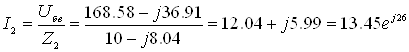А
А
Вычисляем полную, активную и реактивную мощности цепи:
=
Отсюда 
8170.73 В·А; 
7291.56 Вт; 
3687.01 вар.
Реактивная мощность имеет индуктивный характер, так как положительна. Правильность решения можно проверить, составив баланс мощностей, баланс токов / первый закон Кирхгофа / , баланс напряжений / второй закон Кирхгофа / :
7291.56 Вт;
3687.01 вар.
4.87+j3.9 А.
380 В.
Потенциальную векторную диаграмму построим, начиная с вектора
Похожие работы
... соответствующие элементы матрицы равны нулю. Решением уравнения будет , где - матрица, обратная матрице коэффициентов . Использование принципа суперпозиции для анализа электрических цепей. Применяя принцип суперпозиции можно найти ток любой ветви или напряжение любого участка электрической цепи как алгебраическую сумму частичных токов или напряжений, вызываемых отдельным действием источников ...
... Определим погрешности расчета мощности: - для активной мощности - для реактивной мощности Погрешности связаны с округлениями при расчете, они находятся в допустимых пределах. 1.9 Построим лучевую диаграмму токов и топографическую диаграмму напряжений для преобразованной цепи. Определим потенциалы точек. Пусть , т.е. . Тогда (В) Выберем масштаб: ; ; ; ; ...
чает в себя источники мощности (активные элементы) и приемники (пассивные элементы). В качестве пассивного линейного элемента в цепях постоянного тока выступает резистор, имеющий электрическое сопротивление R. Единица измерения Ом. Величина, обратная сопротивлению, называется электрической проводимостью: G = 1/R. Единица измерения См - сименс. В качестве активных элементов - источников ...
... Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно: u=1,2sin(ωt + φ) 4. Электрические цепи при гармоническом воздействии в установившемся режиме Основные свойства линейных цепей: Принципа суперпозиции. Независимыми называют узлы, которые: отличаются одной ветвью. Независимыми называются контура, которые: отличаются одной ...
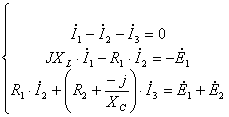
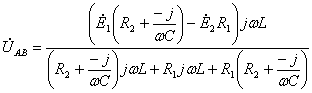
0 комментариев