Навигация
2. Уравнение Блоха
Уравнение Блоха является основой для анализа электромагнитных процессов, возникающих при ЯМР. Оно получено из феноменологических представлений (не физических) и хорошо описывает поведение макросистемы в магнитном поле. Это уравнение имеет вид
![]() . (3)
. (3)
Член ![]() отражает незатухающую прецессию (ротацию), где произведение
отражает незатухающую прецессию (ротацию), где произведение![]() пропорционально w, т.е. 1/t; векторная сумма
пропорционально w, т.е. 1/t; векторная сумма ![]() - поперечная намагниченность; Т1 и Т2 - постоянные времени продольной и поперечной релаксаций. Форма второго и третьего слагаемых уравнения Блоха говорит о том, что процесс релаксации предполагается экспоненциальным. Это допущение справедливо для жидкостных сред (ликворов), однако является весьма приближенным для жиров, серого и белого вещества мозга и совсем далеко от истины для твердых образований, у которых Т1 и Т2 очень малы.
- поперечная намагниченность; Т1 и Т2 - постоянные времени продольной и поперечной релаксаций. Форма второго и третьего слагаемых уравнения Блоха говорит о том, что процесс релаксации предполагается экспоненциальным. Это допущение справедливо для жидкостных сред (ликворов), однако является весьма приближенным для жиров, серого и белого вещества мозга и совсем далеко от истины для твердых образований, у которых Т1 и Т2 очень малы.
Положим, что Т1 и Т2 весьма велики. Тогда вторым и третьим членами в уравнении (3) можно пренебречь. Допустим также, что Н = Н0 и Н = kН0. Тогда уравнение Блоха примет вид
![]() . (4)
. (4)
Начальные значения составляющих М обозначим как ![]() . Представим М в виде
. Представим М в виде ![]() , где i, j, k – орты, и выполним перемножение векторов согласно правилу, которое записано в виде таблицы.
, где i, j, k – орты, и выполним перемножение векторов согласно правилу, которое записано в виде таблицы.
Сравнивая левые и правые части в (4), находим
![]() . (5)
. (5)
Решим систему (4.5), положив ![]() . Знак "минус" здесь необходим для правильного отражения действия градиентных полей, в чем убедимся далее. Дифференцируя первое уравнение системы (5), с учетом второго получаем
. Знак "минус" здесь необходим для правильного отражения действия градиентных полей, в чем убедимся далее. Дифференцируя первое уравнение системы (5), с учетом второго получаем
![]() или
или ![]() .
.![]()
Это уравнение незатухающих колебаний, решение которого с учетом начальных условий можно записать в виде![]()
![]() .
.![]()
Полное решение системы (5) будет иметь вид
![]() ,
,
![]() , (6)
, (6)
![]() .
.
При учете в уравнении Блоха членов, содержащих Т1 и Т2 первое и второе уравнения системы (6) следует умножить на exp(-t/T2), а третье уравнение примет вид
![]() .
.
Из этой формулы видно, что продольная намагниченность является апериодической неосциллирующей функцией.
Поперечную намагниченность можно представить в компактной комплексной форме
![]() или
или ![]() , (7)
, (7)
где ![]() ,
, ![]() .
.
Чтобы понять, как осуществляется управление прецессией, кратко рассмотрим устройство и действие магнитной системы МР-томографа (более подробно речь о ней пойдет впереди). Она представляет собой сложную конструкцию и состоит из главного магнита, градиентных, корректирующих и радиочастотных катушек. Главный магнит служит для создания сильного и однородного магнитного поля. Он может быть выполнен в виде соленоида с током (резистивный магнит). При больших индукциях (свыше 0,5 Тл) потери в таком магните становятся чрезмерно большими. В этом случае применяют сверхпроводящие (криогенные) магниты, охлаждаемые жидким гелием. Их стоимость очень велика, но зато диагностические возможности МР-томографов с такими магнитами намного выше. Применяют также постоянные магниты со слабым полем (0,1- 0,15 Тл).
Корректирующие катушки создают слабые постоянные магнитные поля, предназначенные для компенсации неоднородностей поля главного магнита, которая должна быть не более 10-6 .
Градиентные катушки осуществляют управление процессом выбора и сканирования сечения. При изменении тока в этих катушках очень незначительно меняется основное поле и соответственно изменяется ларморова частота в отдельных точках пространства. Градиентных катушек три: соответственно для создания градиентных полей по осям x, y и z. Особенностью градиентных полей является то, что векторы их напряженностей в любой точке направлены параллельно оси z, т.е. вдоль оси главного магнита, а их абсолютные значения линейно зависят от соответствующей координаты (рис.4).

Рисунок 4. Поля градиентов.
При действии градиентных полей результирующее поле будет равно
![]() или
или ![]() ,
,
где r- обобщенная координата точки. Градиенту G(r) соответствует ларморова частота
w(r) = g(H0+Gr), а величина M(t,r) будет определяться выражением, аналогичным (7):
![]() . (8)
. (8)
Если формировать статический градиент G во время наблюдения сигнала, частота колебаний намагниченности начинает зависеть от r. Эта пространственная зависимость сказывается на характере выходного сигнала. Если сформировать градиентный импульс малой длительности t (t << T1, T2), то в выражении (8) можно пренебречь величиной t/T2(r):
![]() . (9)
. (9)
Величину ![]() в (9) можно рассматривать как изменение фазы колебания с частотой w0. Рассмотрим теперь действие ВЧ магнитного поля H1(t) при наличии поля главного магнита. Как было сказано ранее, это поле возбуждается РЧ катушками в поперечном направлении. Будем считать, что оно направлено вдоль оси х и запишем его в виде
в (9) можно рассматривать как изменение фазы колебания с частотой w0. Рассмотрим теперь действие ВЧ магнитного поля H1(t) при наличии поля главного магнита. Как было сказано ранее, это поле возбуждается РЧ катушками в поперечном направлении. Будем считать, что оно направлено вдоль оси х и запишем его в виде ![]() . Такое поле называют линейно поляризованным. Его можно записать в тождественной форме
. Такое поле называют линейно поляризованным. Его можно записать в тождественной форме
![]() +
+![]() .
.
Это выражение представляет собой сумму полей с круговой поляризацией с разным направлением вращения. Причем, при выборе g со знаком "минус" в уравнении Лармора (w = -gН), вторая составляющая практически не влияет на прецессию ядер и ею можно пренебречь. Таким образом,
![]() .
.
Это поле называется эффективным.
Пусть время действия РЧ импульса намного меньше самой малой постоянной релаксации (минимальное время Т2 тканей составляет 40 мс). Тогда уравнение Блоха будет иметь вид
![]() ,
,
где ![]()
![]() +
+![]() , H = H0 + h, h = Gr – вклад градиентной системы. С учетом правила перемножения векторов найдем
, H = H0 + h, h = Gr – вклад градиентной системы. С учетом правила перемножения векторов найдем
![]() -
- ![]() ,
,
![]() , (10)
, (10)
![]() .
.
Для упрощения решения этой системы введем вращающуюся систему координат i¢, j¢ и k¢= k, которая вращается с частотой прецессии, т.е. синхронно с вектором намагниченности. При этом одна из проекций может быть равной нулю или оказаться постоянной величиной. Преобразование проекций поясняется с помощью рис.5.![]()

Рисунок 5. Преобразование координат
С помощью зависимостей (11), используя уравнения системы (10), можно получить уравнения для вращающейся системы координат
![]()
![]() , (12)
, (12)
![]() .
.
Положим в системе (12) w = w0. Учитывая w0 = – gН0, имеем gН + w0 = g(Н0 +h) – gH0 = gh. Здесь проявляется необходимость введения знака " минус" в уравнении Лармора. Иначе бы gН + w0 » 2w0. Рассмотрим частный случай статического поля (h =0) и воздействия ВЧ поля H1(t). В этом случае система (12) примет вид
![]()
![]() ,
, ![]() . (13)
. (13)
Величина ![]() имеет размерность угловой частоты. Обозначим
имеет размерность угловой частоты. Обозначим ![]() . Тогда решениями уравнений (13) будут
. Тогда решениями уравнений (13) будут
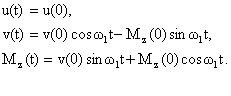 (14)
(14)
Из соотношений (14) видно, что вектор намагниченности вращается вокруг оси i’ c угловой скоростью ![]() . Это вращение относительно медленное и называется нутацией. Угол нутации равен
. Это вращение относительно медленное и называется нутацией. Угол нутации равен 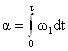 или
или 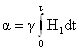 , t - время действия РЧ импульса H1(t). (15)
, t - время действия РЧ импульса H1(t). (15)
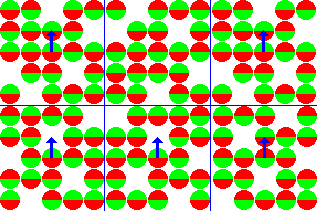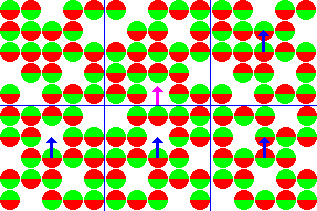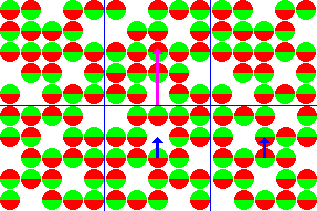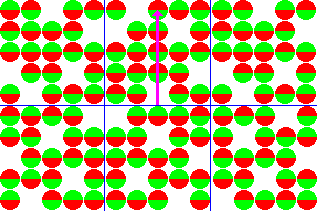
Таким образом, угол нутации зависит от величины и времени воздействия РЧ импульса. Траектория вектора намагниченности при этом подобна раскрывающемуся вееру (рис.6).

Рисунок 6. Нутация вектора намагниченности.
Наиболее часто применяют РЧ импульсы, которые приводят к повороту вектора намагниченности на 90о и на 180о (90о - и 180о - импульсы).
Похожие работы
... плотности на фоне внутривенного введения KB 05-1. МР томография с самого начала своего клинического использования стала методом выбора в визуализации очагов демиелинизации спинного мозга. Как и при исследовании церебральной формы рассеянного склероза, Т2-взвешенные МРТ являются наиболее информативными для выявления очагов демиелинизации в спинном мозге . Т1-взвешенные томограммы полезны в ...
... и костей также прекрасно определяются при МРТ диагностике, но вот состояние полых органов (легких, кишечника, желудка и т.д.) лучше проверять при помощи компьютерной томографии. Принцип МРТ основан на резонировании атомов водорода, а полости, таким образом, аппарату практически неподвластны. Однако при использовании специальной рентгеновской пленки пространственное разрешение рентгеновских ...
... них менее миллиметра. Это обстоятельство позволяет применять многочастотный метод исследования окружающего скважину пространства подобно методу магнитной резонансной томографии (МРТ) в медицине. Возможность работы на нескольких частотах позволяет также увеличить или скорость каротажа, или точность измерения релаксационной кривой при той же скорости, или независимо реализовать несколько различных ...
... и выполняют тончайшие операции. Таких примеров использования КТ, как метод контроля за выполнением хирургических вмешательств, можно привести много. Один из них — применение мобильных компьютерных томографов (Tomoscan M, Philips) в операционных во время хирургических вмешательств, когда, например, топография структур головного мозга после вскрытия черепной коробки и вмешательства на патологическом ...


0 комментариев