Навигация
2. Ошибки репрезентативности
Между характеристиками выборочной совокупности и искомыми параметрами генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой.Общая величина возможной ошибки выборки слагается из ошибок двоякого рода:
- ошибки регистрации;
- ошибки репрезентативности.
Ошибки регистрации свойственны всякому статистическому наблюдению и их появление может быть вызвано несовершенством измерительных приборов, недостаточной квалификацией наблюдателя, недостаточной точностью подсчетов и т.п. Можно полагать, что по сравнению со силошными наблюдениями опасность возникновения ошибок регистрации при выборочном наблюдении должна быть меньше, так как они проводятся более квалифицированными работниками.
Значительно уменьшается при выборочном наблюдении и опасность преднамеренных искажений данных, так как специально подобранные и обученные наблюдатели в них не заинтересованы.
Ошибками репрезентативности называют расхождения между средними величинами или долями признака выборочной и генеральной совокупности. Они присущи только несилошным наблюдениям. Ошибки репрезентативности могут быть:
- систематическими;
- случайными.
Систематическими называются ошибки, которые возникают из-за нарушения научного принципа отбора единиц в выборочную совокупность. Они возникают в тех случаях, когда в результате непрпавильного отбора в выборочную совокупность попали наилучшие или наихудшие единицы.
В результате такого отбора средние и относительные показатели, полученные по выборочной совокупности, будут искаженно характеризовать генеральную совокупность.
Случайные ошибки репрезентативности – это неточности, которые возникают из-за того, что выборочная совокупность не совсем правильно отражает средние величины и величины доли признака генеральной совокупности. Такие ошибки возникают даже при самом строгом соблюдении принципов и правил отбора единиц в выборочную совокупность.
Ошибки репрезентативности свойственны только выборочному наблюдению. Они не могут быть полностью устранены, но они могут быть доведены до незначительных размеров, если соответствующим образом организовать отбор единиц в выборочную совокупность.
Пределы ошибок репрезентативности можно определить с достаточной степенью точности на основании ряда теорем в теории вероятности и математической статистике.
Исключительно важную роль для обоснования и применения выборочного наблюдения играет закон больших чисел. Использование законы больших чисел состоит в том, что при определенных условиях и при достаточно большом объеме наблюдений сводные характеристики, полученные на основе выборочного наблюдения, будут мало отличаться от соответствующих характеристик генеральной доверенности. Основываясь на этом, можно, увеличивая объем выборочной совокупности, уменьшить пределы возможных ошибок репрезентативности, довести их до наименьших размеров. С другой стороны, зная пределы ошибок репрезентативности, можно определить необходимую численность выборочной совокупности.
3. Измерение ошибки выборки
Величина ошибки выборки зависит от численности выборочной совокупности и от степени колеблемости изучаемого признака.
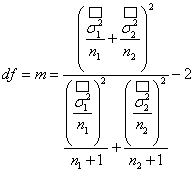
Зависимость величины ошибки выборки: одна формула применяется при выборочном определении средней величины признака, а другая – при выборочном определении доли признака. Доказательства и вывод этих формул даются в курсах математической статистики.
Формула средней ошибки выборки при определении средней величины признака имеет следующий вид:
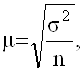
где m - средняя ошибка выборки;
s2 - дисперсия признака в генеральной совокупности;
n – число единиц в выборочной совокупности.
Следовательно, средняя ошибка выборки равна корню квадратному из дисперсии признака, деленной на численность выборочной совокупности. Это значит, что ошибка выборки уменьшается при уменьшении колеблемости признака, а также при увеличении выборочной совокупности. Это означает также, что при уменьшении колеблемости признака можно уменьшить объем выборки.
Формула средней ошибки выборки при определении доли признака такова:
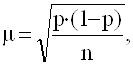
где m - средняя ошибка выборки;
p –доля признака в генеральной совокупности;
n – число единиц в выборочной совокупности.
Вышеприведенные формулы ошибки выборки применяются, когда отбор единиц в выборочную совокупность производится в порядке случайной повторной выборки. Повторная выборка называется потому, что каждая из единиц, отобранная из генеральной совокупности, после регистрации ее признаков возвращается обратно и может при каждом последующем отборе попасть в выборку еще раз, т.е. повторно. Практически случайная повторная выборка встречается сравнительно редко. Большей частью имеют дело со случайной бесповторной выборкой. Бесповторная выборка называется потому, что каждая из единиц после регистрации ее признаков обратно не возвращается и в дальнейшем уже в отборе не существует.
При бесповторной выборке сокращается численность единиц генеральной совокупности. Поэтому при определении ошибки выборочной средней и доли признака при бесповторном отборе должна быть учтена численность генеральной совокупности и доля выборки.
Генеральную совокупность обозначим через N, тогда доля выборочной совокупности n, будет равна ![]() . Поэтому в формулу ошибки выборки при повторном отборе должен быть введен дополнительный множитель
. Поэтому в формулу ошибки выборки при повторном отборе должен быть введен дополнительный множитель 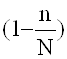 . Тогда формулы ошибок выборки бесповторного отбора примут следующий вид:
. Тогда формулы ошибок выборки бесповторного отбора примут следующий вид:
для определения ошибки выборочной средней:
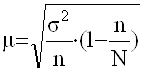
для определения ошибки выборочной доли:
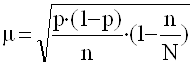
Дополнительный множитель  всегда будет меньше 1. Например, при 20%-ой выборке доля выборочной совокупности
всегда будет меньше 1. Например, при 20%-ой выборке доля выборочной совокупности ![]() =0,2, а дополнительный множитель
=0,2, а дополнительный множитель  =1,0-0,2=0,8.
=1,0-0,2=0,8.
Покажем расчет ошибки выборочной средней и доли признака по данным, приведенным в табл.1.
Отбор участков в примере производится по схеме бесповторной выборки. Из 300 участков было отобрано 30, т.е. доля участков, попавших в выборочную совокупность составляла ![]() =
=![]() =0,1 или 10%. Дополнительный множитель
=0,1 или 10%. Дополнительный множитель  =1,0-0,1=0,9.
=1,0-0,1=0,9.
Определим ошибку средней урожайности по участкам, попавшим в выборку:
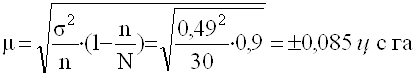
Полученная величина ошибки выборки показывает, что средняя урожайность на участках, попавших в 10% выборку, может на ±0,12 ц с 1 га отличаться от генеральной средней, или, иначе говоря, можно ожидать, что средняя урожайность в генеральной совокупности будет находится между 15,12 (15+0,12) и 14,88 (15-0,12) ц с 1 га.
Ошибка выборочной доли – доли участков с урожайностью 15 и более центнеров с 1 га:
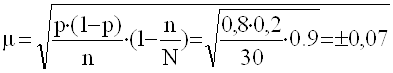
Полученная величина ошибки выборки показывает, что доля участков с урожайностью 15 ц с 1 га в общем числе участков может отклоняться на ±0,07 от доли участков с подобной урожайностью во всей генеральной совокупности.
Можно ожидать, что доля участков с урожайностью 15 и более ц с 1 га будет находится в генеральной совокупности между 0,80 (0,73+0,07) и 0,66 (0,73-0,07).
При этом возникает вопрос: обязательно ли или лишь с определенной степенью вероятности средняя или доля в генеральной совокупности расположатся в диапазонах, определяемых средней ошибкой выборки, с вероятностью 0,683.
Это нас подводит к еще одному показателю ошибки выборки – предельной ошибки выборки.
Предельная ошибка выборки – показатель, характеризующий диапазон, в котором по обе стороны от выборочной средней или выборочной доли расположатся значения генеральной средней или генеральной доли, гарантируемые с определенной степенью вероятности.
Формула предельной ошибки выборки:
D=tm,
где D (дельта) - величина пред. ошибки выборки с заданной вероятностью;
t – коэффициент доверия, которорму соответствуют вероятности предельной ошибки выборки;
m - средняя ошибка выборки.
Величины вероятности, соответствующие коэффициентам доверия, устанавливаются математической статистикой. Так, например, t = 1 соответствует вероятность 0,683; t = 2 соответствует вероятность 0,954; t = 3 – вероятность 0,997 и т.д.
Если нам надо диапазон, в котором расположатся генеральная средняя и генеральная доля, определить с большой степенью вероятности, то этот диапазон должен быть расширен. Так, например, если мы должны вероятность определения этого диапазона в условиях нашего примера довести до 0,997, то среднюю ошибку выборки надо умножить на t = 3,
D = tm = ± 0,12 ц с 1 га ´ 3 = ± 0,36 ц с 1 га.
Это означает, что с вероятностью, равной 0,997, можно гарантировать, что средняя урожайность генеральной совокупности расположится между 15,36 ц (15,0+0,36) и 14,64 ц с 1 га (15,0 - 0,36).
Формулы предельных ошибок выборки:
при повторном отборе:
а) для средней D = tm = t ![]() ,
,
б) для доли D = tm = t ;
;
при бесповторном отборе:
а) для средней D = tm = t 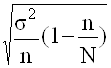 ,
,
б) для доли D = tm = t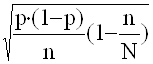 .
.
4. Определение необходимой численности выборки
Одной из наиболее важных и ответственных задач при организации и проведении выборочного наблюдения является установление необходимой численности выборочной совокупности, т.е. такой ее численности, которая обеспечивала бы получение данных, достаточно правильно отражающих изучаемые свойства генеральной совокупности.
При этом должно быть учтено: 1) с какой степенью точности следует получить предельную ошибку выборки; 2) какова должна быть вероятность того, что будет обеспечена обусловленная точность результатов выборочного наблюдения; 3) степень колеблемости изучаемых свойств в исследуемой генеральной совокупности.
Это значит, что необходимая численность выборки (n) устанавливается в зависимости от размеров предельной ошибки выборки (D), от величины коэффициента доверия (t) и от размеров величины дисперсии (s2).
Сами формулы необходимой численности выборки выводятся из формул предельной ошибки выборки следующим образом:
При повторном отборе:
а) для средней
в формуле предельной ошибки выборки
D = t ![]()
обе ее стороны возводим в квадрат
D2 = t2![]()
откуда
D2 = 
и затем
n = 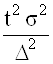
Таким образом, необходимая численность выборочной совокупности равна произведению квадрата коэффициента доверия и дисперсии признака, деленному на квадрат предельной ошибки выборки.
б) для доли:
в формуле предельной ошибки выборки:
D = t ;
;
обе ее стороны возводим в квадрат и получим:
D2 = t2 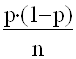
откуда
D2 = 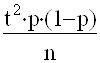
и затем
n = 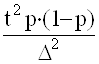 .
.
Таким образом, в этом случае необходимая численность выборочной совокупности равна произведению квадрата коэффициента доверия и дисперсии доли, деленному на квадрат предельной ошибки выборки.
При бесповторном отборе:
а) для средней
в формуле предельной ошибки выборки
D = t 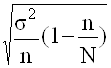 ,
,
после ряда преобразований получаем:
n = 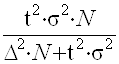 ;
;
б) для доли:
из формулы предельной ошибки выборки:
D = t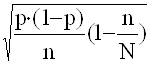 ;
;
после ряда преобразований получаем:
n = 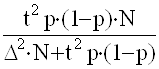 .
.
Пример определения необходимой численности выборочной совокупности исходя из условий повторного отбора. Допустим, что с вероятностью 0,954 требуется определить фактический средний диаметр выпускаемой в одном из цехов детали при условии, что предельная ошибка выборки не должна превышать 0,2 см и зная, что дисперсия размеров диаметра детали составляет 0,5 см. Таким образом:
D = 0,2; s2 = 0,5; t = 2.
В этих условиях:
n = 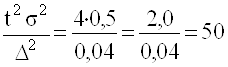 .
.
Следовательно, на выборку в порядке случайного отбора должно быть отобрано 50 деталей. Если всего произведено 5000 таких деталей, то доля выборки составляет ![]() =0,01 или 1%.
=0,01 или 1%.
Так как в данном примере доля выборки очень небольшая, то расчет, полученный по формуле повторной выборки, может быть применен и для выборки бесповторной. Таким образом, для выборочной проверки должна быть отобрана каждая 100-я деталь.
Похожие работы
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... вида выборочного наблюдения; 6) установление сроков проведения наблюдения; 7) определение потребности в кадрах для проведения выборочного наблюдения, их подготовка; 8) оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность. Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и ...
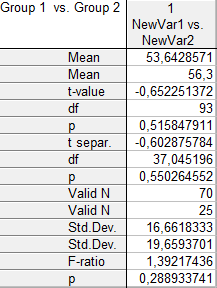
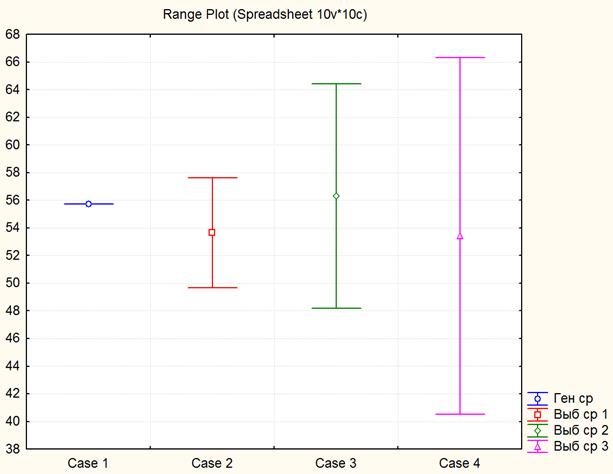
... гипотез о значении генеральной средней и о равенстве двух выборочных средних Для наглядного и компактного представления результатов проведенного выборочного наблюдения необходимо воспользоваться графическими возможностями ППП STATISTICA. Весьма существенным, с дидактической точки зрения, является то, что последовательное выполнение рассматриваемых лабораторных работ, дает возможность ...
... в выборе отдельных типов изучаемого явления. Поэтому можно сказать, что при изучении сложных совокупностей предварительное (выделение групп) является одним из важнейших принципов научной организации выборочного наблюдения. 2.4 Серийный отбор При серийном (гнездовом) отборе выборке подлежат не отдельные единицы совокупности, а целые группы, серии или гнёзда, в состав которых входят единицы, ...
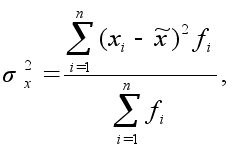
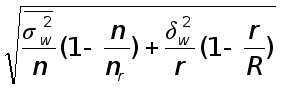
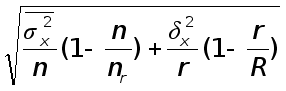
0 комментариев