Навигация
Решение систем линейных уравнений, работа с матрицами
3 Решение систем линейных уравнений, работа с матрицами
Решение систем линейных алгебраических уравнений (СЛАУ).
Пусть задана СЛАУ следующего вида:
a11x1+a12x2+··· + a1nxn=b1,
a21x1+a22x2+··· + a2nxn =b2,
an1x1+an2x2+··· + annxn=bn.
Эту систему можно представить в матричном виде
АХ=b,
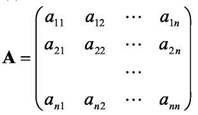
где- матрица коэффициентов системы уравнений;
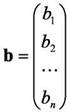
-вектор правых частей

-вектор неизвестных
При выполнении лабораторной работы СЛАУ необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.
Метод обратной матрицы.
Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
А-1Ах=А-1b,
Ex=A-1b, (E единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле x=A-1b.
Метод Крамера.
В этом случае неизвестные x1,x2,… , xn вычисляются по формуле:
![]()
где ∆ - определитель матрицы A, ∆i - определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, где будет храниться результат, и после получения результата необходимо преобразовать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на примере следующей системы
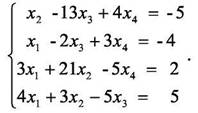
В этом случае матрица коэффициентов А и вектор свободных членов b имеют вид
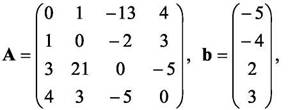
Введём матрицу A и вектор b в рабочий лист MS Excel (см. рис. 21)
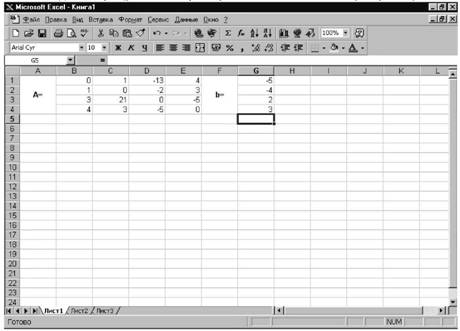
Рисунок 21
В нашем случае матрица А находится в ячейках B1:Е4, а вектор b -G1:G4. Сначала решать систему будем методом обратной матрицы. Поэтому необходимо вычислить матрицу, обратную A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно!!!); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР (функция для вычисления обратной матрицы) (см. рис. 22), и, щелкнув по кнопке OK (Excel 97,2000,XP) или Шаг > (Excel 5 или Excel 7), перейдём ко второму шагу мастера функций. Затем необходимо выделить на рабочем листе исходную матрицу, или просто ввести интервал (в нашем случае B1:E4), где хранится матрица, в качестве параметра в функцию МОБР (см. рис.23).
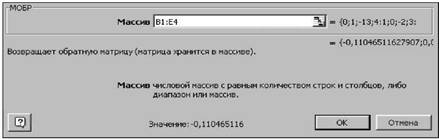
Рисунок 22
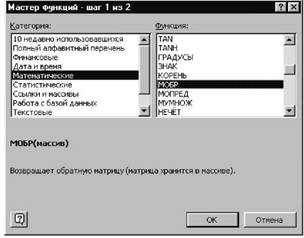
Рисунок 23
Далее щелкаем по кнопке OK, и в первой ячейке выделенного диапазона увидим некое число. Для того, чтобы получить всю обратную матрицу, необходимо выполнить следующие действия: нажать клавишу F2 и затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет следующий вид (см. рис. 24).
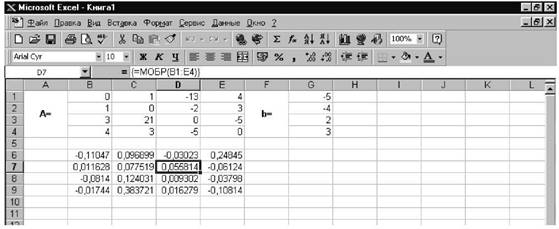
Рисунок 24
Теперь нам осталось умножить полученную обратную матрицу на вектор b. Для этого выделим ячейки, где будет храниться результирующий вектор. В нашем случае пусть это будут ячейки H6:H9. Затем обратимся к мастеру функций, и в категории Математические выберем функцию умножения матриц МУМНОЖ.
Перейдём ко второму шагу мастера функций (см. рис.25).
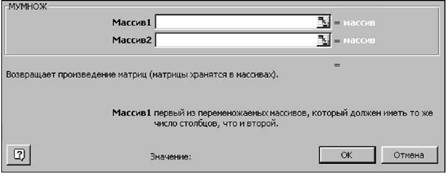
Рисунок 25
В качестве параметров этой функции необходимо передать Массив 1 -первая из перемножаемых матриц, и Массив 2 - вторая перемножаемая матрица. Как известно из курса высшей математики, при умножении матриц важен порядок сомножителей. Теперь определим параметры функции МУМНОЖ в нашем случае. В качестве Массив 1 введём интервал B6:E9 (обратная матрица), в качестве Массив 2 введём интервал G1:G4 (вектор b).
Щёлкаем по кнопке OK, и в первой ячейке выделенного диапазона увидим первое число результирующего вектора. Для того, чтобы получить весь вектор, необходимо выполнить следующие действия: нажать клавишу F2 и затем одновременно клавиши Ctrl+Shift+Enter. В результате в ячейках H6:H9 будет храниться вектор решения системы уравнений.
Осталось сделать проверку. Умножим матрицу A на полученный вектор x и проверим, получится ли вектор b. Умножение матрицы A на вектор x осуществляется аналогично описанной выше процедуре. В результате наш рабочий лист будет иметь вид (см. рис. 26).
Теперь рассмотрим, как можно решить эту же систему методом Крамера. Введём матрицу А и вектор b на второй рабочий лист. Кроме того, сформируем четыре матрицы из матрицы A заменой соответствующего столбца вектором b. Рабочий лист примет следующий вид (см. рис. 27).
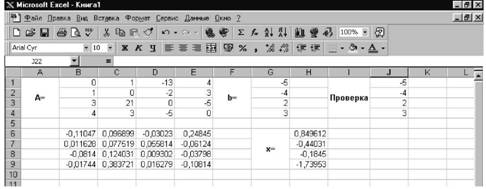
Рисунок 26
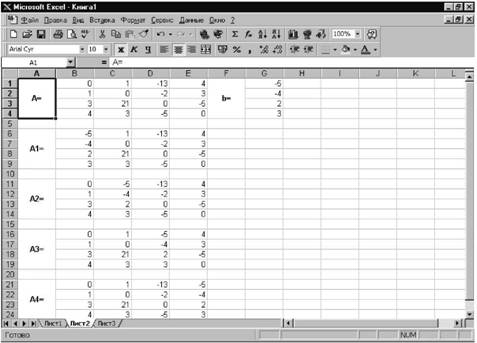
Рисунок 27
Теперь необходимо вычислить определители матриц A, A1 ,A2 ,A3 и A4. Определители в нашем случае будем хранить в ячейках I10-I14. Переведём курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД (это функция вычисления определителя матрицы), перейдём ко второму шагу мастера функций (см. рис. 28). В качестве параметра Массив укажем интервал B1:E4, где хранится матрица A. В ячейки I11-I14 просто введем соответствующие формулы
МОПРЕД(B6:E9), МОПРЕД(B11:E14), МОПРЕД(B16:E19), МОПРЕД(B21:E24)
В результате мы вычислили все необходимые для решения системы определители. Осталось только разделить вспомогательные определители на основной, и мы решим систему уравнений. В ячейку K11 введём формулу
=I11/$I$10
Затем скопируем её содержимое в ячейки K12, K13 и K14. Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с этим именем. Поэтому когда мы протащим формулы из ячейки К11 в ячейки диапазона К12:К14 в них будет найдено значение при соответствующих значениях x, y, т.о. мы создаем таблицу значений . Система решена. В результате рабочий лист имеет вид (см. рис. 29).
При выполнении лабораторной работы вам придется выполнять сложение, вычитание, умножение матриц. Как выполнять умножение, мы уже рассмотрели. Сейчас мы рассмотрим, как оптимальным образом выполнить сложение (или вычитание) двух матриц.
Вычислить
![]()
Введём обе матрицы на рабочий лист: первую - в ячейки A1:B3, вторую в ячейки D1:E3, затем выделим ячейки для результирующей матрицы. Пусть в нашем случае это будут ячейки F1:G3. Затем введём формулу
=A1:B3+D1:E3
Так как эта формула матричная, то затем необходимо перейти в режим редактирования, нажав клавишу F2 и затем одновременно клавиши Ctrl+Shift+Enter. Аналогично можно вычесть две матрицы, умножить матрицу на константу. Для умножения матрицы на число 5 в выделенной области необходимо ввести формулу =A1:B3*5.
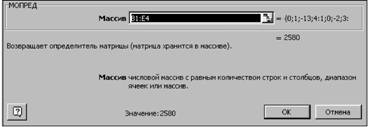
Рисунок 28
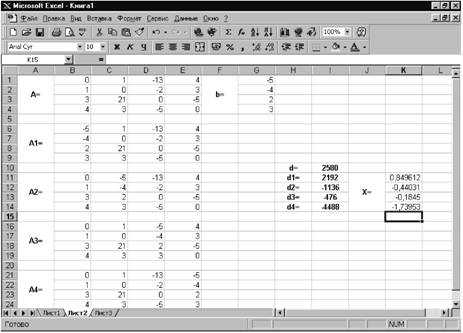
Рисунок 29
Список использованных источников
1. Уокербах Джон. Библия пользователя Exsel 97.Пер. с англ. К.- Диалектика, 1997.
2. Рон Персон. Excel 7.0 для WINDOWS 95: пер. с англ.-СПб.:BHV-Санкт-Петербург,1996.
2. Водополова Н.В. Практическое пособие: “Получение данных в EXCEL из внешних данных” / Водополова Н.В., Косинов Г.П., Шибеко В.Н. – Гомель, 2002.
Похожие работы
... . Устраните различия. Если документ не помещается на одном листе, возможно, следует уменьшить размеры рисунков и надписей. 2. Работа с Microsoft Excel 2.1 Основы работы в MS Excel Знакомство с приложением MS Excel. Приобретение элементарных навыков работы в среде пакета. Ввод и редактирования данных. Основные принципы ввода и редактирования данных изложены во многих книгах по ...
... разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий, учета местных условий. Данная выпускная квалификационная работа посвящена исследованию автоматизации работы в среде MS Office в школьном курсе информатики. Изучение этой темы в общеобразовательной школе вынесено в профильный курс «Информатика и информационные технологии» для 10 - ...
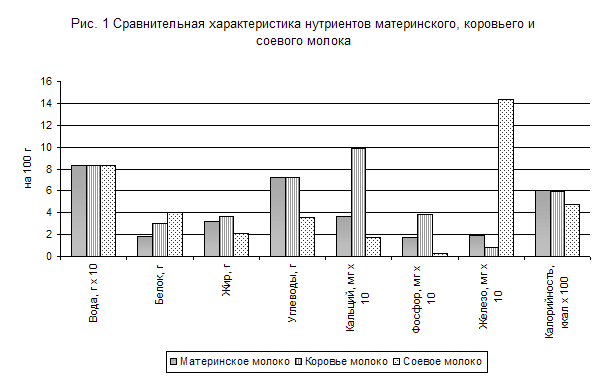
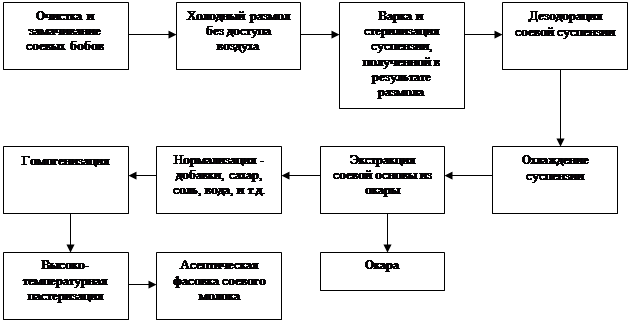
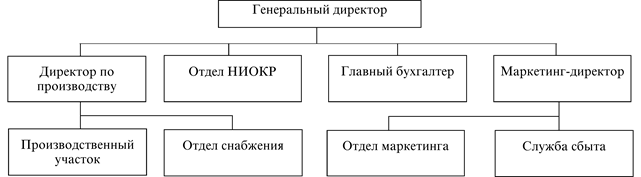
... всех показателей рыночной устойчивости. Такая тенденция с точки зрения кредиторов повышает гарантированность предприятием своих обязательств. Поэтому предприятие имеет возможность реализовать свой бизнес-план по выпуску новой продукции. 3. Бизнес-план производственного предприятия ООО «Украина» по производству соевого молока 3.1. Резюме Предприятие ООО «Украина», организованно в 1997 году и ...
... . Corel WordPerfect Office привлекает другим: непохожестью на Microsoft Office, что избавляет пользователя от его недостатков, но вместо этого приходится мириться с изъянами WordPerfect. Ни одну из альтернативных настольных электронных таблиц нельзя сравнить с Microsoft Excel по глубине функциональности. Однако OpenOffice.org по своим возможностям близок к Excel, а в Corel есть записываемые ...

0 комментариев