Навигация
Метод Эйлера с шагом h/2
2.2 Метод Эйлера с шагом h/2.
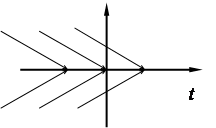
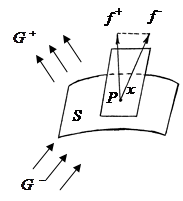
Метод Эйлера допускает простую геометрическую интерпретацию. Пусть известна точка (xi,yi) интегральной кривой уравнения y'=f(x, y).
Касательная к интегральной кривой уравнения, проходящая через эту точку, определяется уравнением
y = yi + f(xi , yi)(x-xi).
Следовательно, вычисленная методом Эйлера точка (xi+1 ,yi+1 ),
Где xi+1=xi+h, yi+1=yi + h f(xi , yi), лежит на этой касательной.
Найдем методом Эйлера на [0, 1] с шагом h=0.2 и с шагом h=0.1 приближенное решение задачи Коши
y' = sin x – cos y, y(0)=1.
Изобразим приближенные решения графически.
Расчетные формулы метода Эйлера для решения этой задачи имеют вид
x0=0, y0= 1, xi+1 = xi + 0.2, yi+1 = yi + 0.2(sinxi - cosyi), i =0, 1, ..., 4
xi+1 = xi + 0.2, yi+1 = yi + 0.2(sinxi - cosyi), i =0, 1, ..., 9
Определим правую часть уравнения
![]()
Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.
Определим диапазон изменения номера точки i=0,1, ..., 4 для вычислений с шагом h=0.2
![]()
Для того чтобы ввести символ диапазона изменения индекса <..>, щелкните по соответствующей позиции в панели Matrix или введите с клавиатуры символ <;> ("точка с запятой")
При решении задачи с шагом h=0.2 назовем шаг h1, аргумент - x1, а решение - y1.
Определим начальное условие
![]()
![]()
Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator
Определим шаг формулы Эйлера - шаг интегрирования
![]()
Определим по формулам Эйлера значения приближенного решения в узлах сетки
![]()
![]()
Выведем в рабочий документ вычисленные значения решения
Для того чтобы вывести значение переменной в рабочий документ, введите имя переменной, знак равенства и щелкните по рабочему документу вне выделяющей рамки
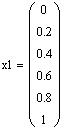
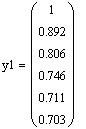
Построим график найденного решения y1(x1)
![]()
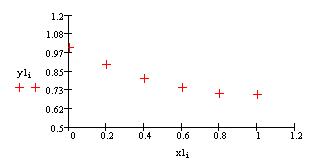
Для того чтобы построить график приближенного решения, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции возле оси абсцисс обозначение компонент вектора, содержащего значения узлов сетки, а в позиции возле оси ординат - обозначение компонент вектора, содержащего значения приближенного решения в узлах сетки; затем щелкните по свободному месту в рабочем документе вне поля графиков.
Определим диапазон изменения номера точки i=0,1, ..., 9 для вычислений с шагом h=0.1
![]()
Для того чтобы ввести символ диапазона изменения индекса <..>, щелкните по соответствующей позиции в панели Matrix или введите с клавиатуры символ <;> ("точка с запятой")
При решении задачи с шагом h=0.1 назовем шаг h2, аргумент - x2, а решение - y2.
Определим начальное условие
![]()
![]()
Для того чтобы ввести нижний индекс переменной, щелкните по соответствующей позиции в панели Matrix или в панели Calculator
Определим шаг формулы Эйлера - шаг интегрирования
![]()
Определим по формулам Эйлера значения приближенного решения в узлах сетки
![]()
![]()
Выведем в рабочий документ вычисленные значения решения. Для сравнения рядом выведены значения решения, вычисленные с большим шагом
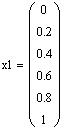
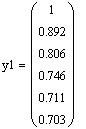


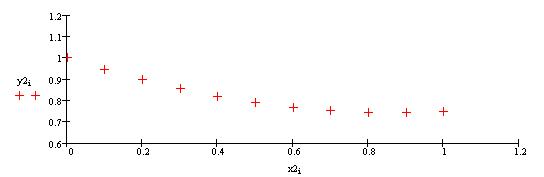
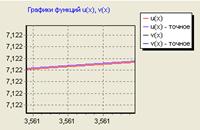
Построим график решения y2(x2)
![]()
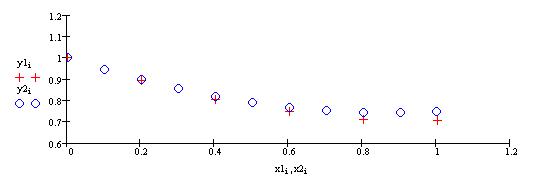
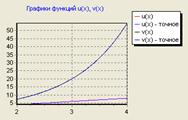
Построим на одном графике оба приближенные решения
![]()
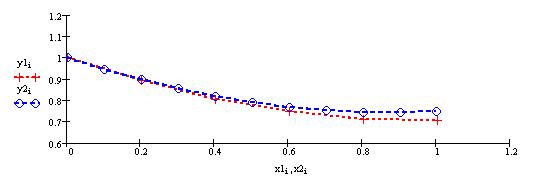
Для того чтобы одновременно построить графики нескольких функций от разных аргументов, щелкните в панели Graph по пиктограмме декартова графика, введите в помеченной позиции у оси абсцисс имя первого аргумента, запятую, имя второго аргумента, и т.д., разделяя имена аргументов запятой.
Аналогично, в позиции возле оси ординат введите имя функции первого аргумента, запятую, имя функции второго аргумента и т.д. разделяя имена функций запятой.
Когда функции определены, щелкните по рабочему документу вне поля графиков.
Похожие работы
... в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений: | ук*-у(хк)|=1/3(yk*-yk), (2.5.9) где у(х)-точное решение дифференциального уравнения. Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//=f(y/,y,x) c начальными условиями y/(x0)=y/0, y(x0)=y0, ...
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... силы взаимодействия между рыбой и рабочими органами машин, поскольку изменяется площадь контакта, обусловливающая силы трения. До настоящего времени структурно-механические характеристики в основном оцениваются органолептическим методом. Рыбу сдавливают пальцами и оценивают ее консистенцию. Не достатком такого метода оценки структурно-механических характеристик мышечной ткани является его ...


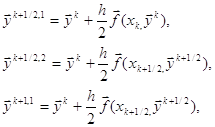
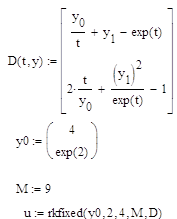
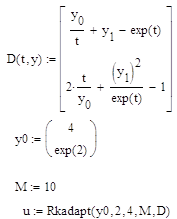
0 комментариев