Навигация
Создание мини-игры "Магический квадрат"
Отдел образования Жлобинского райисполкома
Государственное учреждение образования
«Средняя общеобразовательная школа № 11 г. Жлобина»
Учебно-исследовательская работа по информатике
Создание мини-игры «Магический квадрат»
Выполнила
ученица 8 «А» класса
средней школы № 11 г. Жлобина
Забелова Екатерина
Руководитель:
Чупругина Наталья Анатольевна
учитель информатики
первой категории
СОШ № 11 г. Жлобина
2010г.
Введение
Тема моей научно-исследовательской работы «Создание мини-игры «Магический квадрат»». Я заинтересовалась идеей создания математической мини-игры. Имеющихся у меня знаний языка программирования Pascal оказалось недостаточно, хотя бы потому, что он не позволяет создавать программы с привлекательным и удобным интерфейсом. Передо мной встали две проблемы: 1) методы заполнения квадратной матрицы; 2) выбор языка программирования для реализации игры. Первая проблема легко решилась после изучения соответствующей литературы. Над второй пришлось поработать. Был выбран язык программирования Delphi, ядром которого является Pascal. Изучалась специальная литература, оказали помощь интернет-форумы по некоторым вопросам.
Работа актуальна для тех, кто хотел бы начать овладение языком программирования Delphi. Народная мудрость гласит: «Никого ничему нельзя научить, но всему можно научиться». На примере создания мини игры «Магический квадрат» можно научиться использовать компоненты, оформлять процедуры, менять свойства объектов, обрабатывать события. А практический вид познания – самый эффективный вид познания.
Лично для меня эта работа большой шаг в изучении и, самое главное, в практическом применении языка программирования высокого уровня.
Объектом исследования является программирование на языке Delphi.
Предмет исследования – разработка программ создания мини-игр на языке программирования Delphi.
Целью нашего исследования было:
теоретическое обоснование и разработка программы создания мини игры «Магический квадрат».
Гипотеза исследования:
Если
v проанализировать содержание понятия «магический квадрат» и методы построения магических квадратов;
v проанализировать назначение и возможности Delphi;
v проанализировать пути решения проблем создания мини-игр на языке Delphi;
v разработать программу мини-игры «Магический квадрат»
То это обеспечит
Ø развитие и прикладное применение навыков программирования;
Ø получение навыков программирования в популярной системе программирования Delphi;
Ø неформальное усвоение материала по программированию на языке Delphi.
В соответствии с целью и гипотезой исследования ставились и решались следующие задачи:
Написать программу создания мини-игры «Магический квадрат», которая, во-первых, генерирует поле магического квадрата 3×3 с некоторыми пустыми клетками; во-вторых, проверяет, является ли заполненная квадратная матрица «магическим» квадратом.
Теоретическая часть
МАГИЧЕСКИЙ КВАДРАТ, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 1, а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1, б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 2), изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
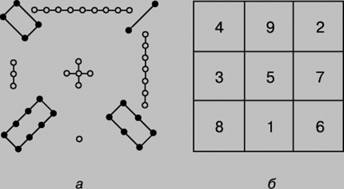
Рис. 1. ЛО-ШУ
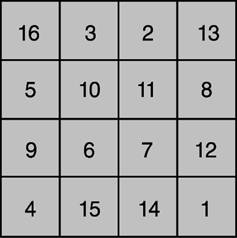
Рис. 2. КВАДРАТ ДЮРЕРА.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел. Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна S = n(n2 + 1)/2. Доказано, что n ≥ 3. Для квадрата 3-го порядка S = 15, 4-го порядка – S = 34, 5-го порядка – S = 65.
Две диагонали, проходящие через центр квадрата, называются главными диагоналями. Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края (такую диагональ образуют заштрихованные клетки на рис. 3). Клетки, симметричные относительно центра квадрата, называются кососимметричными. Таковы, например, клетки a и b на рис. 3.
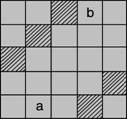
Рис. 3. ЛОМАНАЯ ДИАГОНАЛЬ И КОСОСИММЕТРИЧНЫЕ КЛЕТКИ
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы. Мы рассмотрим ниже только один метод - метод построения магических квадратов нечетного порядка, который и использовали для заполнения матрицы числами.
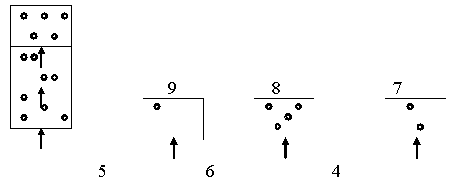
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де ла Лубера. Рассмотрим этот метод на примере квадрата 5-го порядка (рис. 4). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
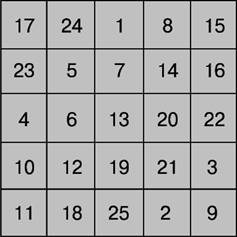
Рис. 4. МЕТОД ДЕ ЛА ЛУБЕРА.
Практическая часть
Выражение «написать программу» отражает только один из этапов создания компьютерной программы, когда разработчик программы (программист) действительно пишет команды (инструкции) на бумаге или при помощи текстового редактора.
Программирование – это процесс создания (разработки) программы, который может быть представлен последовательностью следующих шагов:
1. Спецификация (определение, формулирование требований к программе).
2. Разработка алгоритма.
3. Кодирование (запись алгоритма на языке программирования).
4. Отладка.
5. Тестирование.
6. Создание справочной системы.
7. Создание установочного диска (CD-ROM).
СпецификацияСпецификация, определение требований к программе — один из важнейших этапов, на котором подробно описывается исходная информация, формулируются требования к результату, поведение программы в особых случаях (например, при вводе неверных данных), разрабатываются диалоговые окна, обеспечивающие взаимодействие пользователя и программы.
На этом этапе я определила последовательность этапов создания программы.
1. Создание и оформление окна программы – главной формы.
2. Заполнение полей-клеток магического квадрата (предусмотреть защиту от ввода пользователем символов, кроме чисел).
3. Проверка квадратной матрицы на предмет, является ли она магическим квадратом.
4. Оформление диалогового окна «Магический квадрат», вызываемого одноименной командой главного меню.
5. Оформление диалогового окна «Правила игры», вызываемого одноименной командой главного меню.
Подобрала информацию необходимую для создания программы. Определила, как должен выглядеть результат (Рисунок 5).
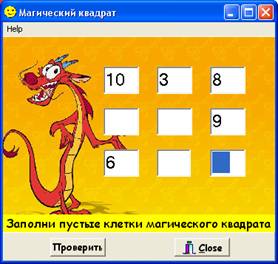
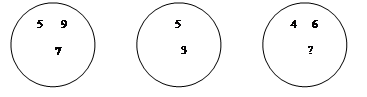
Рис. 5. «МАГИЧЕСКИЙ КВАДРАТ»
Разработка алгоритмаНа этапе разработки алгоритма необходимо определить последовательность действий, которые надо выполнить для получения результата. Если задача может быть решена несколькими способами и, следовательно, возможны различные варианты алгоритма решения, то программист, используя некоторый критерий, например скорость решения алгоритма, выбирает наиболее подходящее решение. Результатом этапа разработки алгоритма является подробное словесное описание алгоритма или его блок-схема.
Далее приводится словесное описание алгоритма
1. Создание и оформление окна программы – главной формы
1.1 Выбор и размещение на форме компонентов
В Object Inspector на вкладке Properties значение свойства Position установить PoScreenCenter – для того, чтобы после запуска программы, форма появлялась в центре экрана. Name – Form1.
В редакторе Image Editor создать Icon File, нарисовать смайлик. Сохранить в файле Icon1.ico. В Object Inspector на вкладке Properties справа от свойства Icon щелкнуть мышью и в окне выбора файла иконы загрузить созданный файл.
Компоненты вкладки Standart:
1.1.1 TMainMenu – главное меню формы, Name – MainMenu1 (Содержит один пункт меню «Help» (Name – Help1) с двумя пунктами подменю «Магический квадрат» (Name – N1) и «Правила игры» (Name – N2)).
После установки компонента на форму создать пункт меню «Help». Для этого дважды щелкнуть на компоненте левой кнопкой мыши, в окне инспектора объектов вводим название пункта меню «Help» в строке свойства Caption, нажимаем клавишу Enter. Для создания пунктов подменю щелкнуть мышью в окне конструктора меню ниже пункта меню «Help», набрать «Магический квадрат», Enter, набрать «Правила игры», Enter. Чтобы связать с выбором пункта меню нужное действие, определяем процедуру обработки его события OnClick – вызов соответствующего диалогового окна.
1.1.2 TPanel – панель, Name – Panel1 (Для размещения кнопок). Значение свойства Align выбираем alBottom, чтобы панель разместить внизу формы. Свойство Caption очистить.
1.1.3 TButton – кнопка (Одна кнопка «Проверить», вторая, расположенная над ней, «Начать»). Кнопку Button1 размещаем на панели, Name – Button1. Свойство Caption – «Проверить». Кнопку Button2, Name – Button2, размещаем на кнопке Button1. Свойство Caption – «Начать».
1.1.4 TLabel – метка (Для вывода текста комментариев действий пользователя). Метку Label размещаем на форме. Name – Lb1. Свойство Caption очистить. Значение свойства Align выбираем alBottom. Свойство Color – clYellow. С помощью свойства Font корректируем шрифт.
Компоненты вкладки Additional:
1.1.5 TBitBtn – кнопка с изображением (Кнопка Close для закрытия окна); Name – BitBtn1. Кнопка Close размещается на панели. Свойство Kind – bkClose. Значение bkClose определяет типовой значок, надпись Close на кнопке, а также типовую функцию закрытия окна, которая будет связана с этой кнопкой.
1.1.6 TMaskEdit – поле с маской ввода (9 полей с маской ввода только цифровой информации). Устанавливаем ниже перечисленные значения свойств для всех девяти полей. Name – MEd1 .. MEd9. Раскрываем диалоговое окно свойства EditMask. В поле Input Mask вводим следующую последовательность символов: 9999;1;. В поле Character for Blanks вместо умалчиваемого символа-заполнителя, которым является символ подчеркивания (_), указываем пробел и закрываем окно.
1.2 Процедура обработки события OnPaint (для того, чтобы сделать рисунок с расширением .bmp фоновым). Свойство Bitmap содержит ссылку на объект класса TBitmap. Перед загрузкой объекта Bitmap его надо создать. Метод StretchDraw() растягивает или сжимает картинку так, чтобы она заполнила всю форму.
1.3 Процедура обработки события OnCanResize (запрещающая изменение размеров формы).
1.4 Процедура обработки события OnActivate (программно задаем заголовок формы, обеспечиваем показ кнопки «Начать», скрываем кнопку «Проверить»).
2. Заполнение полей-клеток магического квадрата
2.1 Процедура обработки события OnClick кнопки Button2 («Начать»).
2.1.1 Процедура zapolnenie(x,y:integer) (По входящему параметру х заполняет клетки квадрата, по входящему параметру у одним из четырех способов очищает некоторые клетки, выводит в метке соответственную надпись, показывает кнопку «Проверить», прячет кнопку «Начать»).
2.1.2 В теле главной процедуры проверяем, была ли ситуации «Попробуй еще раз» (z=true). Если была, то вызываем процедуру zapolnenie(x,y:integer) со старыми значениями х и у; если нет (z=false), генерируем у – способ удаления клеток, х – начальное число х. Заполняем матрицу.
Похожие работы
... дидактических игр на уроках математики, анализ игровой деятельности Изучив теоретические материалы по развитию мотивации познавательной деятельности, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики активизирует познавательную деятельность учащихся, автором работы в 6 «б» ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
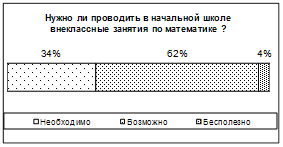
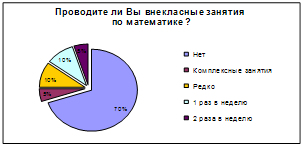
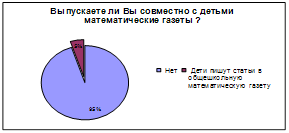
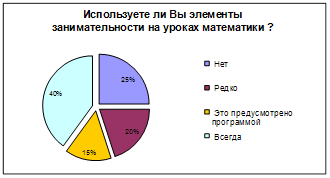
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...




0 комментариев