Навигация
Общие сведения об электромагнитах
2.2 Общие сведения об электромагнитах
Электромагнитом называется всякое железное, стальное или чугунное тело (сердечник), могущее быть временно намагниченным посредством пропускания электрического тока по проводнику (обмотка), окружающему это тело.
Вокруг всякого проводника, по которому проходит электрический ток, возникает магнитное поле, характер которого может быть описан указанием расположения и распределения магнитных силовых линий этого поля. Если проводник представляет тонкую проволоку значительной длины, то магнитные силовые линии созданного вокруг проволоки поля представляют вокруг каждой точки проволоки систему концентрических кругов, расположенных вокруг проволоки, как вокруг оси в соответствии с рисунком 2.1.
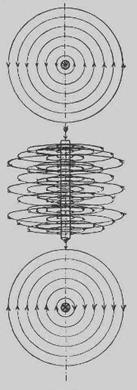
Рисунок 2.1 – Магнитные силовые линии электромагнита
Направление линий сил (направление поля; то направление, в котором двигался бы вокруг проволоки свободный северный магнитный полюс) зависит от направления тока в проволоке; направление линий сил в зависимости от направления тока определяется следующим правилом если мы будем глядеть вдоль тока так, чтобы ток уходил от нас, то линии сил будут направлены по направлению движения часовой стрелки.
Сила поля в данной точке его (число линий сил, пересекающих площадку в 1 квадратный сантиметр, расположенную в данной точке перпендикулярно к направлению линий сил) растет пропорционально силе тока, проходящего по проволоке; уменьшается по мере удаления от проволоки пропорционально расстоянию от проволоки (закон Био и Савара, 1820 г.) и может быть выражена через
![]() (2.1)
(2.1)
где H – сила поля в динах (или число линий на 1 см2);
J – сила тока в амперах;
А – расстояние проволоки в см.
Если проволока представляет не прямую, а какую-нибудь линию в плоскости или пространстве, то характер поля её вообще будет иной, зависящий от формы проволоки. Так, если проволока согнута в плоское кольцо, то расположение линий сил будет таково, какое показано в одной из диаметральных плоскостей кольца в соответствии с рисунком 2.2.
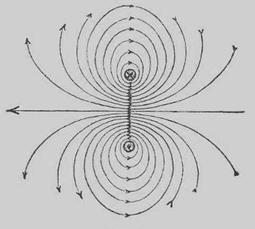
Рисунок 2.2 – Расположение линий сил для проволоки, согнутой в кольцо
Сила поля в какой-либо точке на оси кольца, радиусом в R см, отстоящей на а см от плоскости кольца, равна
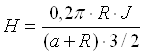 (2.2)
(2.2)
Если проволока навита спирально вокруг кругового цилиндра (соленоид), то поле внутри её состоит из пучка почти параллельных и равномерно густо расположенных линий сил, расходящихся по мере приближения к концу соленоида и охватывающих его со всех сторон; линии сил в одной из плоскостей сечения соленоида, проходящей через его ось располагаются в соответствии с рисунком 2.3.
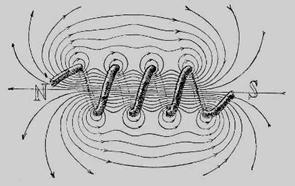
Рисунок 2.3 – Линии сил в плоскости сечения, проходящей через ось соленоида
Чем ближе расположены друг к другу отдельные витки соленоида, чем большее число витков приходится на единицу длины соленоида и чем больше длина соленоида, тем более параллельны по направлению и равномерны по густоте распределения линии сил внутри соленоида, т.е. тем однороднее до силе и направлению будет магнитное поле внутри соленоида.
Если на таком соленоиде длины L см расположено N витков проволоки, по которым проходит ток силой в J ампер, то число линий сил на площадку в 1 квадратный сантиметр, расположенную перпендикулярно к линиям сил внутри соленоида, или сила поля внутри соленоида, может быть выражена формулой
![]() (2.3)
(2.3)
Если соленоид по меньшей мере в 6 раз длиннее диаметра составляющих его витков, то приведенная формула (2.3) дает с точностью до 1% силу поля той части внутри соленоида, которая отстоит по меньшей мере на 2 диаметра от концов соленоида.
Направление линий сил, пронизывающих соленоид, может быть определено по выше приведенному правилу для прямолинейного проводника, но еще проще по ниже следующему правилу: если мы будем глядеть на конец соленоида, и ток будет кружить по виткам его до направлению движения часовой стрелки, то линии сил внутри соленоида будут направлены от нас внутрь соленоида; если ток идет по виткам против направления часовой стрелки, то линии сил идут изнутри соленоида к нам. Количество линий сил, пронизывающих соленоид, или магнитный поток Ф, пронизывающий его, равняется:
![]() (2.4)
(2.4)
где H – сила поля внутри соленоида (число линий сил на 1 см2);
S – сечение соленоида в см2.
По характеру внешнего поля, создаваемого им, соленоид качественно и количественно совершенно подобен магниту в соответствии с рисунком 2.4, из которого выходит Ф линий сил, т.е. на полюсах которого находится Ф/4 π единиц количества магнетизма.
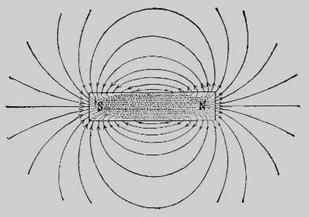
Рисунок 2.4 – Линии сил постоянного магнита
По аналогии с магнитом тот конец соленоида, из которого выходят линии сил, можно назвать северным полюсом соленоида, а тот конец, в который входят линии сил, – южным полюсом. И во внешних своих проявлениях соленоид, обегаемый током, совершенно подобен магниту: будучи подвешен, он устанавливается в магнитном меридиане; разноименные полюсы двух соленоидов притягиваются, одноименные отталкиваются; на железо, на магнитную стрелку соленоид действует как магнит.
Таким образом, соленоид является магнитом, которого магнитные свойства можно по желанию возбудить и уничтожить и внутреннее однородное поле которого нам доступно. Такой соленоид-магнит не может, однако, даже в исключительных условиях сравниться по силе даже с самыми обыкновенными стальными магнитами.
Действительно, если мы предположим даже, что на 1 см длины соленоида приходится, например, 20 оборотов (N/L = 20) и что J = 10 ампер, то H будет равно (2.3) всего только около 250, между тем как стальные магниты средней силы дают магнитный поток, соответствующий H, равному около 1000.
Магнитный поток, даваемый соленоидом, можно значительно увеличить, если заполнить пространство внутри его сильно магнитным веществом – железом, сталью, чугуном. Такой соленоид с железным стержнем (сердечником) внутри его представляет электромагнит в соответствии с рисунком 2.5; ему можно придать самые различные формы, из которых две основные – стержневой электромагнит и подковообразный электромагнит.
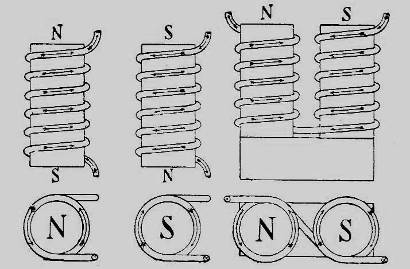
Рисунок 2.5 – Положение полюсов электромагнита
Положение полюсов у электромагнита определяется по тому же самому правилу, как и у соленоида: если глядеть на полюс, и ток течет вокруг него по направленно движения часовой стрелки в соответствии с рисунком 2.5, то это – полюс южный, если против движения часовой стрелки, то это – полюс северный. Магнитный поток, исходящей из электромагнита, может быть сделан чрезвычайно большим; в некоторых практически достигнутых случаях из 1 см2 плоскости полюса выходило до 40000 линий сил (или индукции).
Число, показывающее во сколько раз увеличился магнитный поток от заполнения соленоида железом, не есть величина постоянная при данном соленоиде, данной силе тока и данном сорте железа, а зависит в сильной мере от формы железного сердечника, близости его полюсов друг от друга и т.д.
Причины, влияющие на величину магнитного потока, исходящего из электромагнита, не поддавались анализу, и посему предвычисление электромагнита с данными свойствами было почти невозможно, пока Роулэнд, Бозанке и их последователи не ввели в рассмотрение этого вопроса нового понятия о «магнитной цепи»; к краткому изложению этого понятия и перейдем.
Магнитный поток Ф, возникающий внутри соленоида, Ф = НS, может быть, согласно формуле (2.3), написан в виде
![]()
![]() (2.5)
(2.5)
Магнитный поток состоит из линий сил, исходящих из одного полюса, замыкающихся через окружающее пространство и внутреннюю полость соленоида, в соответствии с рисунком 2.3, и образующих, таким образом, замкнутую магнитную цепь. Поток Ф тем больше, чем больше числитель формулы (2.5) 0,4π NJ; в этом числителе стоит произведение NJ (ампер-обороты), являющееся причиной возникновения магнитного потока; числитель 0,4π NJ называют поэтому магнитодвижущей силой цепи.
Поток Ф тем меньше, чем больше знаменатель L/S, который, подобно электрическому сопротивлению, пропорционален длине пути магнитного тока (внутри соленоида) и обратно пропорционален сечению этого пути; по аналогии выражение L/S – называют магнитным сопротивлением воздушного пути внутри соленоида.
Таким образом, устанавливается аналогия между законом Ома для электрической цепи и правилом (2.5) магнитной цепи: сила электрического тока (величина магнитного потока) прямо пропорциональна электродвижущей силе (магнитодвижущей силе) и обратно пропорциональна электрическому (магнитному) сопротивлению цепи.
Относительно выведенной этим путем аналогии необходимо сделать следующие оговорки:
а) эта аналогия чисто формальная, так как по природе своей явление тока не может быть уподоблено явлению магнитного потока;
б) в качестве сопротивления магнитной цепи соленоида нужно было бы поистине считать не только сопротивление воздушного столба внутри соленоида, но и сопротивление всего окружающего соленоид воздушного пространства, через которое замыкаются линии сил.
Но сопротивление этого пространства (внешнее сопротивление), в виду безграничной протяженности его, обыкновенно столь ничтожно в сравнении с сопротивлением (внутренним) воздушного столба внутри соленоида, что им можно пренебречь. Этим сопротивлением нельзя пренебречь, если внутреннее магнитное сопротивление само ничтожно мало (широкий, короткий соленоид), и это сказывается тем, что формула (2.4), как уже было упомянуто, к этому случаю не может быть применена; абсолютно точна она лишь для случая, когда и внутреннее сопротивление бесконечно велико по сравнению с внешним.
Возможен и другой случай, когда формула (2.5) будет совершенно точна: возьмем длинный тонкий соленоид и согнем его по кругу так, чтобы одна выходная плоскость его наложилась на другую; мы получим тогда расположенную по кольцу соленоидальную обмотку, внутри которой будут протекать все возникающие линии сил, не выходя наружу; в этом случае внешнего сопротивления вовсе нет и формула (2.5) вполне применима.
Из принятой нами аналогии вытекают затем следующие следствия:
а) проводя аналогию между магнитным сопротивлением (L/S) столба воздуха и электрическим сопротивлением R проводника
![]() (2.6)
(2.6)
где k – удельная проводимость вещества проводника,
Мы полагаем удельную магнитную проводимость воздуха равной единице. Магнитную удельную проводимость принято называть проницаемостью; проницаемость воздуха равна единице.
б) Для того, чтобы заставить пройти магнитный поток Ф путь сечением S кв. см и длиной в L см, необходимо число ампер-оборотов
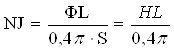 (2.7)
(2.7)
Т. е. на каждый сантиметр пути необходимо число ампер-оборотов
![]() (2.8)
(2.8)
Аналогично с этим необходима определенная разность потенциалов на каждый сантиметр длины проводника, чтобы возбудить в нем электрический ток определенной плотности (определенной силы на каждый квадратный сантиметр сечения).
Если мы заменим всю воздушную магнитную цепь соленоида веществом, у которого проницаемость μ больше, чем у воздуха, например, железом, то магнитное сопротивление уменьшится в μ раз, а поток Ф увеличится в μ раз. Для этого случая формула (2.5) примет вид
![]() (2.9)
(2.9)
Число линий сил, пронизывающих 1 квадратный сантиметр плоскости, перпендикулярной к линиям сил, тоже увеличится в μ раз и будет, направлена, внутрь соленоида не H, а
![]() (2.10)
(2.10)
величину B называют магнитной индукций. Если мы заполним железом только внутреннюю полость соленоида, то ввиду значительной проницаемости железа (доходит до μ = 3000) внутреннее магнитное сопротивление настолько уменьшится, что внешним воздушным сопротивлением нельзя будет пренебречь сравнительно с внутренним, и формула (2.9) сделается неприменимой.
Она останется применимой:
а) если, несмотря на введение железа, внутреннее сопротивление очень велико (соленоид очень длинный и тонкий)
б) если соленоид представляет сплошную замкнутую кольцевую обмотку.
Последний случай практически наиболее важный, и мы в дальнейшем только его и будем рассматривать. Опыт показывает, что формула (2.9) с достаточной для практики точностью применима и тогда, когда сплошной замкнутый железный сердечник не по всей длине обмотан проволокой в соответствии с рисунком 2.6; в этом случае не все линии сил потока проходят через железо, а часть замыкается и через воздух, но, ввиду огромной сравнительно с воздухом проницаемости железа, эта утечка магнитных линии сил столь ничтожна, что в практических расчетах ею часто можно пренебречь.
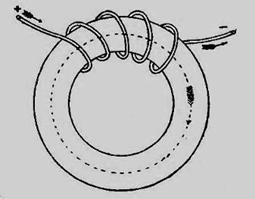
Рисунок 2.6 – Силовые линии сплошного замкнутого железного сердечника, не по всей длине обмотанного проволокой
Применяя к данному случаю формулу (2.9), мы убеждаемся, аналогично вышеизложенному, что необходимое число ампер-оборотов для того, чтобы заставить пройти индукцию В через 1 см пути с проницаемостью μ:
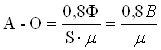 (2.11)
(2.11)
Так, например, если бы мы желали достичь индукцию В = 12000 в электромагните в соответствии с рисунком 2.7 с железным путем в 30 см, и нам известно было бы, что при данной индукции проницаемость железа μ = 900, то, согласно (2.11), нам потребовалось бы для этого 0,8 (12 000/900) 30 = 320 ампер-оборотов, т.е. обмотку в 320 оборотов, до которой проходил бы ток в 1 ампер, или обмотку в 160 оборотов и ток в 2 ампера и т.д.
Слишком малое число оборотов нельзя взять, так как в этом случае обмотка будет занимать слишком малую часть сердечника, и утечка будет слишком велика.
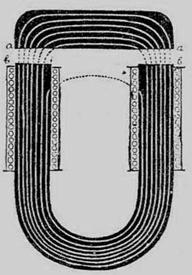
Рисунок 2.7 – Разомкнутая магнитная цепь
Из теории магнитного поля, данной Максвеллом, следует, что две соприкасающиеся плоскости, сквозь которые проходит индукция B, притягивают друг друга с силой в
![]() (2.12)
(2.12)
где S – число квадратных сантиметров в плоскости соприкосновения.
Если в упомянутом выше электромагните в соответствии с рисунком 2.7 полная плоскость соприкосновения якоря с полюсными поверхностями электромагнита равняется 20 кв. см, то нужно было бы употребить силу в 12000 2 х 20/ 8π 981000 = около 120 кГ, чтобы оторвать якорь от электромагнита.
Приподнимем якорь над полюсными поверхностями электромагнита в соответствии с рисунком 2.8.
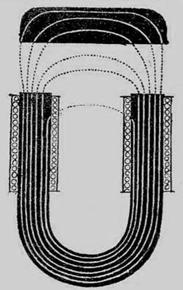
Рисунок 2.8 – Якорь, поднятый над полюсными поверхностями электромагнита
Вследствие этого:
а) увеличится магнитное сопротивление цепи, так как к первоначальному сопротивлению прибавится еще сопротивление двух воздушных слоев ab;
б) уменьшится соответственно увеличению сопротивления поток
![]() (2.13)
(2.13)
где 2l – удвоенная высота воздушного слоя;
в) увеличится утечка линий сил.
Если l очень невелико, то мы можем предположить, что ширина пути, занимаемого потоком в воздушных слоях, равна толщине железа электромагнита, и что утечка столь незначительна, что ею еще можно пренебречь на практике, и на этих основаниях пользоваться формулой (2.13). Она дает
NJ = (ФL/ Sμ + 2 Фl/ S) 0,8 = 0,8 В (L/ μ + 2l),
т.е. для достижения того же В мы к выше полученному числу ампер-оборотов должны прибавить еще число ампер-оборотов, необходимое для того, чтобы заставить пройти индукцию В через слой воздуха 2l.
Если мы опять пожелали бы получить В = 12000, а l было бы равным только 1 мм, то нам потребовалось бы, благодаря огромному сопротивлению, введенному двумя тонкими воздушными слоями, уже не 360, а 2280 ампер-оборотов!
Если бы мы удалили якорь на значительное расстояние в соответствии с рисунком 2.9, то утечка очень сильно возросла бы, поток сильно ослабел бы и, вследствие неопределенности величины утечки и сопротивления воздушных частей пути линий сил, всякий расчет сделался бы невозможным.
Отсюда видно, что расчет электромагнита на основании принципа магнитной цепи возможен лишь тогда, когда электромагнит с его якорем представляет почти замкнутую магнитную цепь, и результат применения правила магнитной цепи становится тем более сомнительным, чем больше сопротивление воздушных слоев сравнительно с сопротивлением железного пути.

Рисунок 2.9 – Отведение якоря на значительное расстояние
В наиболее важных на практике случаях (электромагниты у динамо-машин и двигателей, электромагниты в телеграфных приборах, часах и т.д.) мы имеем дело с почти замкнутыми магнитными цепями, и применением правила магнитной цепи возможно. Но и в этих случаях, если мы желаем достичь некоторой точности расчета, приходится на основании опытов или вычислений приблизительно определять, какой процент возникающих в соленоиде линий сил утекает, и принимать эти данные в соображение при расчете. Лишь в случае электромагнита, держащего приложенный к нему якорь в соответствии с рисунком 2.7, расчет по приведенному выше образцу дает достаточную для технических целей точность.
Пользуясь правилом магнитной цепи, необходимо иметь ввиду, что проницаемости сильно магнитных веществ не есть величина постоянная, но в сильной мере зависит от силы магнитного поля, в которое помещены эти вещества.
Поэтому применение закона магнитной цепи возможно лишь в том случае, если зависимость проницаемости от силы поля известна для всех веществ (железо, сталь, чугун), входящих в конструкцию данного электромагнита. Данные для различных веществ располагаются обыкновенно в таблицах или кривых, в которых дается зависимость между силой поля H и индукцией.
В этих же таблицах для облегчения расчета дается обыкновенно и число ампер-оборотов на 1 см пути данного материала при данной индукции. В качестве примера ниже приведены некоторые данные для лучшего мягкого железа, литой стали и чугуна.
Таблица 2.1 – Параметры для веществ
Железо мягкое
| H | μ | B | A.-O. на 1 см |
| 1,4 | 2760 | 4000 | 1,16 |
| 1,9 | 3160 | 6000 | 1,52 |
| 2,5 | 3200 | 8000 | 2,00 |
| 3,4 | 2940 | 10000 | 2,74 |
| 5,2 | 2310 | 12000 | 4,16 |
| 13,5 | 1040 | 14000 | 10,80 |
| 44,0 | 364 | 16000 | 36,20. |
Сталь литая
| 2,3 | 1740 | 4000 | 1,84 |
| 3,1 | 1900 | 6000 | 2,52 |
| 4,0 | 2000 | 8000 | 3,20 |
| 5,3 | 1890 | 10000 | 4,24 |
| 8,4 | 1430 | 12000 | 6,72 |
| 15,4 | 910 | 14000 | 12,32 |
| 42,5 | 376 | 16000 | 34,00 |
Чугун
| 2,4 | 834 | 2000 | 1,92 |
| 3,5 | 857 | 3000 | 2,80 |
| 5,5 | 728 | 4000 | 4,40 |
| 9,9 | 505 | 5000 | 7,92 |
| 20,0 | 300 | 6000 | 16,00 |
| 42,0 | 167 | 7000 | 33,60 |
Если магнитная цепь электромагнита состоит из ряда частей, составленных из различных магнитных материалов, то правило магнитной цепи напишется в наиболее общем виде
Ф = 0,4 π NJ/ (L1/S1 μ 1 + L2/S2 μ 2 + L3/S3 μ 3 +…) (2.14)
где L1, L2, L3… – длины пути магнитного потока в этих частях;
S1, S2, S3… – сечения этих путей;
μ 1, μ 2, μ 3… – проницаемости данных материалов при данных индукциях B1 = Ф/S1, B2 = Ф/S2, B3 = Ф/S3… в них.
Полное число ампер-оборотов, необходимое для получения потока Ф, получится как сумма, необходимых для путей L1, L2, L3… при индукциях B1, B2, B3….
Если магнитная цепь разветвляется, как это часто имеет место в электромагнитах динамо-машин, то расчет ведется аналогично расчетам разветвлений электрического тока, так как, в виду полной аналогии между правилом магнитной цепи и законом Ома, все следствия из закона Ома (с надлежащими в каждом частном случае ограничениями) могут быть применяемы и к магнитной цепи.

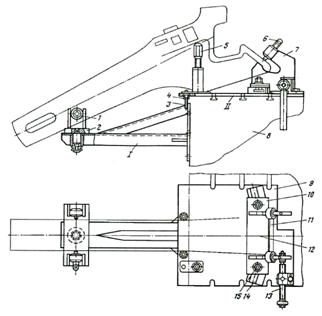
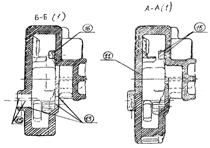
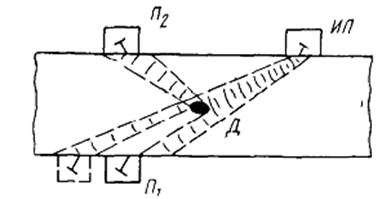
Рисунок 2.10 – Электромагнит Дю-Буа
Катушки N и M создают поток, который замыкается через железные бока и основание рамы ОКО'; поле создается в пространстве с. Сердечники N и M просверлены и снабжены по концам никелевыми призмами а и b для наблюдений над магнитным вращением плоскости поляризации в веществах, помещенных в поле. H – коммутатор, посредством которого можно менять направление тока в обмотке электромагните и тем самым изменять направление потока и поля в пространстве с.
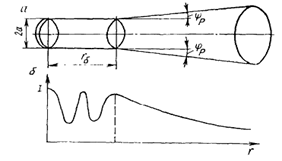
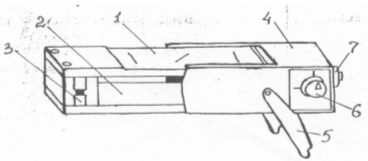
Электромагнит Румкорфа не отличается рациональностью конструкции, так как длинные и относительно тонкие железные части боков и основания его представляют сравнительно большое магнитное сопротивление. Значительно более совершенен электромагнит, сконструированный в недавнее время Дю-Буа в соответствии с рисунком 2.10; MM NN представляет обмотку; поле получается в а, между конически отточенными полюсными наконечниками; в СС сердечники просверлены для магнито-оптических наблюдений.
Изображенный электромагнит несет около 2500 оборотов проволоки и при 20 амперах дает поле в 35000 линий сил на кв. см на протяжении воздушного слоя в 1 мм длиной и около 30 кв. мм сечением. Посредством подобного электромагнита Дю-Буа достигал силы поля выше 40000 линий на кв. см. К этой же группе могут быть отнесены электромагниты, применяемые в электромагнитных тормозах, основанных на индукции токов в металлических массах, движущихся в магнитном поле.
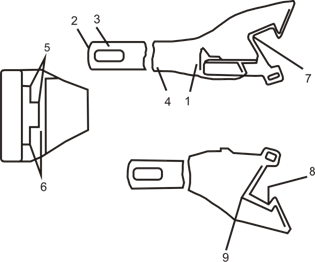
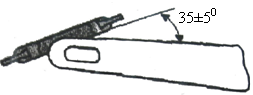
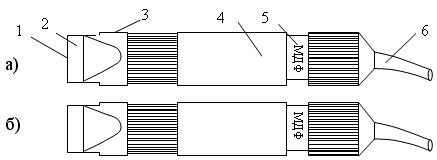
Электромагниты для приставания, назначением которых является удерживать якорь, оттягиваемый грузом или пружиной в соприкосновении с полюсами до тех пор, пока по обмотке электромагнита проходит ток, и отпускать его, когда ток прекратится. Сюда относятся электромагниты, применяемые во многих электрических кранах и лебедках, электромагниты, применяемые для сцепления отдельных частей механизмов в желаемый момент (тормоза, механизмы для сцепления валов), а также электромагниты, применяемые во многих хронографах. Все эти электромагниты, представляя почти замкнутую магнитную цепь, легко поддаются расчету; для того, чтобы удерживательная их сила, рассчитанная по формуле (2.12), была возможно большой, необходимо по возможности уменьшать их магнитное сопротивление, конструируя их из толстых коротких железных частей в соответствии с рисунком 2.11.
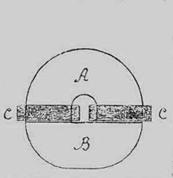
Рисунок 2.11 – Конструкция электромагнитов, применяемых в кранах и лебедках
A – сердечник;
В-якорь;
СС – обмотка.
Опыт показал, что даже в лучшем железе практически трудно достичь индукции выше 14–16000 линий на кв. см; отсюда следует на основании формулы (2.12), что наибольший груз, который может держать 1 кв. см полюсной поверхности электромагнита, будет равняться в лучших условиях от 8 до 10 кГ.
Электромагниты для притяжения якоря на расстоянии находят наибольшее применением (телеграфы, звонки, прерыватели, электрические часы, реле, хронографы, телефоны и т.д.).
В виду большого сопротивления, представляемого воздушными слоями между полюсными наконечниками и якорем, величина магнитного сопротивления железной части цепи играет меньшую роль, и поэтому сердечники могут быть в случае надобности более тонкими и длинными. В виду большого общего магнитного сопротивления цепи индукция даже при значительном числе ампер-оборотов не может быть большой, и притягательная сила электромагнита на якорь всегда сравнительно незначительна.
Интересное видоизменение этого типа представляют поляризованные электромагниты (предложены Юзом в 1855 г.), в которых сердечники поддерживаются все время сильно намагниченными при помощи сильных стальных магнитов.
Такие электромагниты представляют две особенности:
а) Сила, с которой они притягивают якорь, зависит от направления тока в обмотке электромагнита; действительно, если магниты сердечника всегда обладают определенной индукцией B, то пропускание тока по обмотке в том направлении, которое усиливает эту индукцию, увеличит силу притяжения якоря; обратное направление тока ослабит притяжение. На этом свойстве поляризованных электромагнитов основано применение их в тех электромагнитных приборах, в которых направление движения якоря должно меняться с изменением направления тока, проходящего по обмотке электромагнита (электрические звонки для переменного тока).
б) Незначительная сила тока в обмотке электромагнита вызывает большее изменение притягательной силы, чем в обыкновенном электромагните Действительно, предположим, что сила тока в обмотке такова, что она может возбудить поле, H = 2,3; тогда в обыкновенном электромагните с сердечником из литой стали возникнет индукция 4000 и пропорциональная квадрату её или 16 сила притяжения. Если же сердечник был уже предварительно намагничен до В = 6000, то усиление его намагничевания при помощи поля H = 2,3 вызовет приблизительно индукцию около 10000; при пропускании тока сила притяжения, следовательно, увеличится от 6 2 = 36 до 10 2 = 100, т.е. на 100–36 = 64, что в 4 раза больше, чем в неполяризованном электромагните. В виду этого свойства поляризованные электромагниты применяются во всех тех случаях, когда ничтожный по силе ток должен вызвать заметное изменение в силе притяжения якоря (реле, телефоны).
Магниты для отделения сильно магнитных материалов от немагнитных веществ, к которым первые примешаны. Электромагниты этого рода находят теперь большое применение в обогащении железных руд; измельченная железная руда бежит струёй мимо электромагнита, который втягивает в свое поле все сильно магнитные части руды, содержащие железо, и пропускает мимо несодержащие железо минеральные составные части руды. Сюда же можно отнести электромагниты, применяемые в медицине для извлечения из различных частей тела (в особенности, глаз) врезавшихся в них железных частичек.
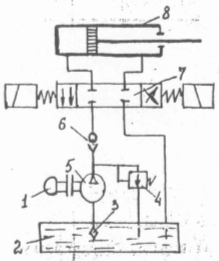
Электромагниты с подвижным сердечником, в которых при пропускании тока через обмотку соленоида подвижной железный сердечник втягивается в соленоид. Подобные электромагниты применяются во многих измерительных и регулирующих инструментах и в регуляторах дуговых ламп.
Придавая сердечнику соответственную форму, стараются достичь того, чтобы сила втяжения сердечника на значительном протяжении его пути была по возможности одинакова.
Похожие работы
... участка. Принимаем процент узлов и деталей, поступающих в ремонт на условиях кооперации из эксплуатационного депо для тележечного участка =30% Принимаем программу для тележечного участка 1000 ед. 2. Совершенствование технологии контроля автосцепочного устройства 2.1 Виды и порядок осмотра автосцепочного устройства Автосцепное устройство подвижного состава должно постоянно находиться ...
... шт. 12. Футляр укладочный 3. Капиллярный метод Различают три основных метода капиллярной дефектоскопии: люминесцентный, цветной и люминесцентно-цветной. Капиллярный метод неразрушающсго контроля качества сварных соединений основан на капиллярном проникновении дефектоскопических материалов в дефекты и их контрастном изображении в оптическом излучении. На сварной шов наносят специальную ...
... износы при перемещении вагонов, исключить возможность саморасцепов и увеличить межремонтные сроки. 4. БЕЗОПАСНОСТЬ И ЭКОЛОГИЧНОСТЬ РЕШЕНИЙ ПРОЕКТА 4.1 Обеспечение безопасности работ на контрольном пункте автосцепки Ремонт пассажирских вагонов производят в вагонном депо, специализирующимся на ремонте цельнометаллических вагонов, в соответствии с руководством и инструкциями по деповскому ...
... профессии Разряд работ Количество работников 1. Мастер 10 1 2. Бригадир (освобожденный) 7 2 3. Машинист моечной установки 3 2 4. Слесарь по ремонту подвижного состава 5 2 5. Слесарь по ремонту подвижного состава 4 1 6. Слесарь по ремонту подвижного состава 3 7 7. Уборщик производственных и служебных помещений 2 3 8. Электросварщик ручной сварки. 5 4 ...

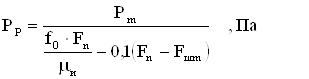
0 комментариев