Навигация
О «мягких» и «твердых» пузырьках в жидкости
33556
знаков
0
таблиц
4
изображения
3. О «мягких» и «твердых» пузырьках в жидкости
«Мягкие» — значит легко деформируемые внешней силой, «твердые» — значит не поддающиеся ее воздействию. Будем придерживаться этих, не очень строгих определений и попытаемся применить их к газовым пузырям в жидкости.
Решим вначале задачу о связи между числом атомов газа, заключенных в пузыре, и его радиусом R, полагая при этом, что жидкость, в объеме которой расположен пузырь» находится под постоянным давлением р0. В поисках интересующей нас связи мы будем считать, что пузырь «равновесный», или лучше сказать «уравновешенный», а это означает, что его стенка не перемещается ни от центра пузыря, ни к его центру. В этом случае давление заключенного в нем газа, 
, стремящегося раздуть пузырь, компенсируется давлением, приложенным к жидкости извне, Р0, и лапласовским давлением, которое обусловлено искривленностью поверхности пузыря 
. Эти два давления вместе стремятся сжать пузырь.
Давление газа 
, заключенного в пузыре, можно определить из закона Менделеева — Клайперона, известного из школьного курса физики
,
где 
— число молекул газа в пузыре. Так как 
, то
.
Равенство растягивающего и сжимающего давлений, осуществляющееся в условиях равновесия, запишем следующей главной формулой:
, или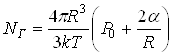 
.
Записанная формула и выражает интересующую нас связь между NT и R.
Та внешняя сила, которой можно «щупать» пузырь для того, чтобы выяснить «мягкий» он или «твердый», определяется давлением Р0. Его можем изменять по собственному желанию. Если 
, то, изменяя 
(разумеется, не нарушая неравенства), мы никак не повлияем на размер пузыря, который сильно сжат собственным, лапласовским давлением, значительно большим, чем внешнее. То есть, если радиус пузыря настолько мал, что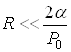
— внешнее давление пренебрежимо мало по сравнению с лапласовским и поэтому до тех пор пока это неравенство сохраняется, пузырь сохранит свой радиус. А это и значит, что он твердый! А вот в случае, когда 
, лапласовское давление значительно меньше внешнего и поэтому любое давление будет приводить к изменению радиуса пузыря. Больше давление — меньше радиус, меньше давление — больше радиус. Это — «мягкий» пузырь, он чувствует внешнее давление. Увеличивая внешнее давление, его можно сжать.
Для того чтобы наши рассуждения обрели количественную меру, оценим радиус пузыря 
, который сжимается лапласовским давлением, равным внешнему . Такой пузырь является как бы пограничным между «мягкими» и «твердыми» пузырями. Если внешнее давление равно атмосферному, то
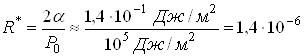м.
Итак, «твердые» пузыри в воде — это те, радиус которых значительно меньше микрометра, а «мягкие» — это те, радиус которых значительно больше микрометра.
«Мягкие» и «твердые» пузыри отличаются не только размерами. Оказывается, что во многих реальных ситуациях они обнаруживают различные свойства и различное поведение.
Для «мягкого» пузырька, когда лапласовским давлением можно пренебречь, из главной формулы следует 
. Это означает, что при объединении двух «мягких» пузырей будут суммироваться их объемы, так как суммируется число газовых молекул. Из этого обстоятельства проистекают два важных следствия.
Во-первых, оно означает, что объем образовавшегося пузыря равен сумме объемов объединившихся.
Во-вторых, оказывается, что два объединившихся пузыря имеют поверхность меньшую, чем та, которую они имели до объединения. Действительно, условие суммирования объемов двух пузырей, радиусы которых 
и 
, означает, что
.
Это равенство можно переписать в иной форме:
.
Так как 
, то
.
Именно в этом неравенстве и содержится энергетическое оправдание объединения «мягких» пузырей: энергия заключенного в них газа не меняется, а связанная с ними поверхностная энергия уменьшается. Так что в процессе слияния общая энергия уменьшается — слияние «мягких» пузырей энергетически выгодно.
Теперь о слиянии «твердых» пузырей. Для них из главной формулы следует 
. Это значит, что при слиянии таких пузырей суммируются не их объемы, а поверхности:
.
При этом объем суммарного пузыря должен превосходить сумму объемов слившихся пузырей:
.
Вывод: при слиянии «твердых» пузырей поверхность, а значит, и энергия поверхности, остаются неизменными. Казалось бы, и объединяться им нечего. Есть, однако, оправдание процесса слияния твердых пузырей. Оно заключается в том, что слиянию пузырей сопутствует расширение газа.
Похожие работы
... мочевого пузыря, особенно осложненных шоком, малоинформативная, так как концентрация контрастного вещества недостаточна для выявления затеков мочи. Диагностическое значение цистоскании при травмах мочевого пузыря невелико. Оно ограничено сложностью укладки больного в уролоческое кресло (шок, переломы костей таза), невозможностью заполнения мочевого пузыря при наличии разрыва, интенсивной ...
... опасно, т.к. быстрая гибель микроорганизмов в таком случае приведет к массивному выбросу эндотоксинов и эндотоксическому шоку. Операция на поврежденных органах Характер оперативного вмешательства при абдоминальной травме зависит от ее вида и поврежденного органа. Печень. При небольших линейных ранах для выполнения гемостаза применяют П-образные швы, которые следует накладывать в поперечном ...
... вскипающей жидкости от давления на входе при стационарном истечении. Сравнение расчетных данных с экспериментальными. Предполагается, что предлагаемый подход к моделированию стационарного и нестационарного истечения вскипающих жидкостей позволит получить полезную информацию и детализировать сопутствующие тепломассообменные и гидродинамические процессы. Обозначения d -диаметр канала; L - ...
... микоплазм представляют собой группу повышенного риска по развитию у них неопластического процесса, однако эти вопросы требуют дальнейшего изучения. Хламидийная инфекция в акушерстве и гинекологии В. Н. Прилепская, И. Ю. Абуд Инфекции, вызываемые микроорганизмом Chlamydia Trachomatis (СТ), в настоящее время признаны одними из наиболее распространенных заболеваний, передаваемых половым путем ...
0 комментариев