Тема 1
Задача 1
Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
| 2 | 4 | 4 | 7 | 6 | 5 | 2 | 2 | 3 | 4 |
| 4 | 3 | 6 | 5 | 4 | 7 | 6 | 6 | 5 | 3 |
| 2 | 4 | 2 | 3 | 5 | 7 | 4 | 3 | 3 | 2 |
| 4 | 5 | 6 | 6 | 10 | 4 | 3 | 3 | 2 | 3 |
Построить вариационный, ранжированный, дискретный ряд распределения, обозначив элементы ряда.
Решение:
Ранжированный вариационный ряд:
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
| 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 10 |
Дискретный вариационный ряд:
|
| 2 | 3 | 4 | 5 | 6 | 7 | 10 |
|
| 7 | 9 | 9 | 5 | 6 | 3 | 1 |
|
| 7/40 | 9/40 | 9/40 | 5/40 | 6/40 | 3/40 | 1/40 |
![]() – варианты,
– варианты, ![]() – частоты,
– частоты, ![]() =
=![]() /(7+9+9+5+6+3+1)=
/(7+9+9+5+6+3+1)=![]() /40
/40
Тема 2
Задача 1
В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.
| Марка автомобиля | Число проданных автомобилей |
| Skoda | 245 |
| Hyundai | 100 |
| Daewoo | 125 |
| Nissan | 274 |
| Renault | 231 |
| Kia | 170 |
| Итого | 1145 |
Решение:
Показатель структуры (ОПС):
ОПС = Число проданных автомобилей / 1145
Skoda 245/1145=0.214
Hyundai 100/1145=0.087
Daewoo 125/1145=0.109
Nissan 274/1145=0.239
Renault 231/1145=0.203
Kia 170/1145=0.148
| Марка автомобиля | Число проданных автомобилей | Доля в продажах (%) |
| Skoda | 245 | 21.4 |
| Hyundai | 100 | 8.7 |
| Daewoo | 125 | 10.9 |
| Nissan | 274 | 23.9 |
| Renault | 231 | 20.3 |
| Kia | 170 | 14.8 |
| Итого | 1145 | 100 |
Тема 3
Задача 1
Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
| ВУЗы города | Общее число студентов (тыс. чел.) | Из них удельный вес (%), обучающихся на коммерческой основе. |
| УГТУ—УПИ | 15 | 15 |
| УрГЭУ | 3 | 10 |
| УрГЮА | 7 | 20 |
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Решение:
1) Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе (%): (15+10+20)/3=15 %
Число студентов, обучающихся в этих трёх ВУЗах на коммерческой основе в сумме: 15*0.15+3*0.1+7*0.2=2.25+0.3+1.4=3.95 тыс. чел.
2) Число студентов ВУЗов, обучающихся на коммерческой основе в среднем: 3.95/3=1.317 тыс. чел.
Тема 4
Задача 1
При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
| Размер месячного вклада, рубли | Число вкладчиков | |
| Банк с рекламой | Банк без рекламы | |
| До 500 | 3 | |
| 500-520 | 4 | |
| 520-540 | 17 | |
| 540-560 | 11 | 15 |
| 560-580 | 13 | 6 |
| 580-600 | 18 | 5 |
| 600-620 | 6 | |
| 620-640 | 2 | |
| Итого | 50 | 50 |
Определить:
1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада;
2) средний размер вклада за месяц для двух банков вместе.
3) Дисперсию вклада для 2-х банков, зависящую от рекламы;
4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы;
5) Общую дисперсию используя правило сложения;
6) Коэффициент детерминации;
7) Корреляционное отношение.
Решение:
(0+500)/2=250, (500+520)/2=510, (520+540)/2=530, (540+560)/2=550,
(560+580)/2=570, (580+600)/2=590, (600+620)/2=610, (620+640)/2=630.
| Размер месячного вклада, рубли | Средний размер месячного вклада, рубли | Число вкладчиков | |
| Банк с рекламой | Банк без рекламы | ||
| До 500 | 250 | 3 | |
| 500-520 | 510 | 4 | |
| 520-540 | 530 | 17 | |
| 540-560 | 550 | 11 | 15 |
| 560-580 | 570 | 13 | 6 |
| 580-600 | 590 | 18 | 5 |
| 600-620 | 610 | 6 | |
| 620-640 | 630 | 2 | |
| Итого | 50 | 50 | |
1) Для банка с рекламой средний размер вклада за месяц составил:
(550*11+570*13+590*18+610*6+630*2)/50=580 руб.
Для банка без рекламы средний размер вклада за месяц составил:
(250*3+510*4+530*17+550*15+570*6+590*5)/50=528,4 руб.
Для банка с рекламой дисперсия вклада будет:
![]() =((550-580)²*11+(570-580)²*13+(590-580)²*18+(610-580)²*6+
=((550-580)²*11+(570-580)²*13+(590-580)²*18+(610-580)²*6+
+(630-580)²*2)/50=(900*11+100*13+100*18+900*6+2500*2)/50=23400
/50=468
Для банка без рекламы дисперсия вклада будет:
![]() =((250-528,4)²*3+(510-528,4)²*4+(530-528,4)²*17+(550-528,4)²*15+
=((250-528,4)²*3+(510-528,4)²*4+(530-528,4)²*17+(550-528,4)²*15+
+(570-528,4)²*6+(590-528,4)²*5)/50=
= (232519,68+1354,24+43,52+6998,4+10383,36+18972,8)/50=
= 270272/50=5405,44
2) Средний размер вклада за месяц для двух банков вместе:
(250*3+510*4+530*17+550*(11+15)+570*(13+6)+590*(18+5)+610*6+63
0*2)/(50+50)=(750+2040+9010+14300+10830+13570+3660+1260)/100=55
4,2 руб. (или (580+528,4)/2=554,2 руб.)
3) Дисперсия вклада для 2-х банков, зависящая от рекламы:
![]() =((550-554,2)²*11+(570-554,2)²*13+(590-554,2)²*18+
=((550-554,2)²*11+(570-554,2)²*13+(590-554,2)²*18+
+(610-554,2)²*6+(630-554,2)²*2)/50=
=(17,64*11+249,64*13+1281,64*18+3113,64*6+5745,64*2)/50=
=56682/50=1133,64
4) Дисперсия вклада для 2-х банков, зависящая от всех факторов, кроме рекламы:
![]() =((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-554,2)²*15+
=((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-554,2)²*15+
+(570-554,2)²*6+(590-554,2)²*5)/50=
=(92537,64*3+1953,64*4+585,64*17+17,64*15+249,64*6+1281,64*5)/50
=303554/50=6071,08
5) Определить общую дисперсию используя правило сложения:
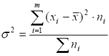
![]() =((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-
=((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-
554,2)²*(11+15)+
+(570-554,2)²*(13+6)+(590-554,2)²*(18+5)+(610-554,2)²*6+(630-
554,2)²*2)/
/100=(277612,92+7814,56+9955,88+458,64+4743,16+29477,72+18681,84+
+11491,28)/100=360236/100=3602,36
Тема 5
Задача 1
Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
| Группы предприятий по объему продукции, тыс. руб. | Число предприятий (f) |
| До 100 100-200 200-300 300-400 400-500 500 и > | 28 52 164 108 36 12 |
| итого | 400 |
Определить:
1) по предприятиям, включенным в выборку:
а) средний размер произведенной продукции на одно предприятие;
б) дисперсию объема производства;
в) долю предприятий с объемом производства продукции более 400 тыс. руб.;
2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
а) средний объем производства продукции на одно предприятие;
б) долю предприятий с объемом производства продукции более 400 тыс. руб.;
3) общий объем выпуска продукции по области.
Решение:
| Группы предприятий по объему продукции, тыс. руб. | Средний объём продукции на группу, тыс. руб. | Число предприятий (f) |
| До 100 100-200 200-300 300-400 400-500 500 и > | 50 150 250 350 450 550 | 28 52 164 108 36 12 |
| итого | 400 |
1) Средний размер произведенной продукции на одно предприятие:
(50*28+150*52+250*164+350*108+450*36+550*12)/400=110800/400=
=277 тыс. руб.
Дисперсия объема производства:
![]() =((50-277)²*28+(150-277)²*52+(250-277)²*164+(350-277)²*108+
=((50-277)²*28+(150-277)²*52+(250-277)²*164+(350-277)²*108+
+(450-277)²*36+(550-277)²*12)/400=4948400/400=12371
Доля предприятий с объемом производства продукции более 400 тыс. руб.:
(36+12)/400= 0,12 или 12%
2) Определить в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
а) средний объем производства продукции на одно предприятие:
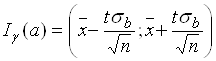
![]() 111,225
111,225
Величина t определяется по таблице значений функции Лапласа из равенства
![]() .
.
Следовательно, в нашем случае последнее равенство принимает вид
Ф(t)=0,954/2=0,477.
Из этого равенства по таблице значений интегральной функции Лапласа ![]() находим значение t=2,00.
находим значение t=2,00.
√n=√400=20
Найдём нижний предел:
![]()
277-2*111,225/20=265,8775 тыс. руб.
Найдём верхний предел:
![]()
277+2*111,225/20=288,1225 тыс. руб.
Iγ(a)=( 265,8775 ; 288,1225)
б) долю предприятий с объемом производства продукции более 400 тыс. руб.:
Средняя: (450+550)/2=500 тыс. руб.
Найдём нижний предел:
![]()
500-2*111,225/20= 488,8775 тыс. руб.
Найдём верхний предел:
![]()
500+2*111,225/20= 511,1225 тыс. руб.
Iγ(a)=( 488,8775 ; 511,1225)
3) Общий объем выпуска продукции по области:
50*28+150*52+250*164+350*108+450*36+550*12=110800 тыс. руб.
Тема 6
Задача 1
Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
| периоды площадь под картофелем | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| До изменения границ района | 110 | 115 | 112 | ||||
| После изменения границ района | 208 | 221 | 229 | 234 | 230 |
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.
Решение:
208/112=1,857 – коэффициент
110*1,857=204.27
115*1,857=213.55
115/112*100=102,68%
110/112*100=98,21%
221/208*100=106,25%
229/208*100=110,096%
234/208*100=112,5%
230/208*100=110,58%
| периоды площадь под картофелем | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| До изменения границ района | 110 | 115 | 112 | ----- | ----- | ----- | ----- |
| После изменения границ района | ----- | ----- | 208 | 221 | 229 | 234 | 230 |
| Сомкнутый ряд | 204.27 | 213.55 | 208 | 221 | 229 | 234 | 230 |
| Сомкнутый ряд относительных величин в % к 3 периоду | 98,21 | 102,68 | 100,0 | 106,25 | 110,096 | 112,5 | 110,58 |
Тема 7
Задача 1По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели
| Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
| II квартал | III квартал | IV квартал | |
| Цена | ? | +10 | -2 |
| Натуральный объем продаж | Без изменения | ? | +5 |
| Товарооборот в денежном выражении | +8 | +5 | ? |
Решение:
Найдём в III квартале ip – так как 110-100=10% (+10) в этой ячейке, то значение индекса запишем 110/100=1,1 По аналогии заполним все ячейки.
| Индексы | Значения индексов | ||
| II квартал | III квартал | IV квартал | |
| ip | x | 1,1 | 0,98 |
| iq | 1,0 | y | 1,05 |
| Ipq | 1,08 | 1,05 | z |
Теперь найдём x,y,z:
Ipq= ip* iq
x= Ipq / iq=1,08/1=1,08 (+8)
y=1,05/1,1=0,95 (-5)
z=0,98*1,05=1,03 (+3)
Таблица примет вид:
| Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
| II квартал | III квартал | IV квартал | |
| Цена | +8 | +10 | -2 |
| Натуральный объем продаж | 0 | -5 | +5 |
| Товарооборот в денежном выражении | +8 | +5 | +3 |
Тема 8
Задача 1
По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.
| Табельный номер рабочего | Разряд (y) | Выработка продукции за смену, шт. (x) |
| 1 2 3 4 5 | 6 2 3 5 4 | 130 60 70 110 90 |
Решение:
Линейное уравнение связи:
y=a+bx
6=a+130*b, a=6-130*b
5=a+110*b, a=5-110*b
6-130*b=5-110*b; 6-5=130*b-110*b; 1=20*b; b=1/20=0,05
6=a+0,05*130; a=6-0,05*130; a=-0,5
Линейное уравнение примет вид:
y=-0,5+0,05x
Проверка:
4=-0,5+0,05*90, 4=4; 3=-0,5+70/20, 3=3; 2=-0,5+60/20, 2=2,5 –
работник 2-го разряда перевыполняет норму и не вписывается в общую зависимость.
Коэффициент корреляции:
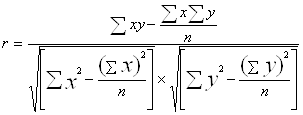
Найдём числитель (n=5):
(2*60+3*70+4*90+5*110+6*130)-(2+3+4+5+6)*
*(60+70+90+110+130)/5=2020-20*460/5=180
Σx²-(Σx)²/n=(60²+70²+90²+110²+130²)-(60+70+90+110+130)²/5=
=45600-211600/5=45600-42320=3280
Σy²-(Σy)²/n=(2²+3²+4²+5²+6²)-(2+3+4+5+6)²/5=90-400/5=90-80=10
r=180/√3280*√10=180/181,1077=0,99388
По шкале Чеддока связь классифицируется как функциональная. Поскольку (0,99388>0,99100), модель надёжна, связь статистически значима.
Тема 9
Задача 1
Имеются следующие данные за 2006 год:
· Численность населения, тыс. чел.: на 1 января - 430,0; на 1 апреля - 430,2; на 1 июля 430,3; на 1 октября - 430,7; на 1 января 2007 г. 430,8
· Число умерших, чел. - 8 170
· Число выбывших на постоянное жительство в другие населенные пункты, чел. - 570
· Коэффициент жизненности - 1,075
· Доля женщин в общей численности населения, % - 58
· Доля женщин в возрасте 15-49 лет в общей численности женщин, % -39
Определите: коэффициенты рождаемости, смертности, естественного, механического и общего прироста населения; число родившихся; число прибывших на постоянное жительство из других населенных пунктов; специальный коэффициент рождаемости.
Решение:
Коэффициент рождаемости
![]() :
:
N – кол-во родившихся, S – численность населения.
Средняя численность населения:
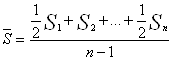 =
=
=(430/2+430,2+430,3+430,7+430,8/2)/(5-1)=
=1721,6/4=430,4
N=430,8-430,0=0,8 тыс. чел. (800 чел.) – За весь 2006 г.
n=1000*0,8/430,4=1,859 (чел./тыс. чел.)
Коэффициент смертности
![]() :
:
M – кол-во умерших.
m=1000*8,17/430,4=18,982 (чел./тыс. чел.) – за 2006 г.
Коэффициент естественного прироста населения
![]() :
:
Kn-m=1,859-18,982=-17,123 (чел./тыс. чел.)
Коэффициент механического прироста населения
![]() :
:
Коэффициент выбытия населения:
![]() =1000*0,57/430,4=1,324 (чел./тыс. чел.)
=1000*0,57/430,4=1,324 (чел./тыс. чел.)
Коэффициент прибытия населения:
![]() =0
=0
(В условиях задачи не указано сколько прибыло населения или чему равен Kпр, решение с двумя неизвестными невозможно. Будем считать его равным 0)
![]() =0-1,324=-1,324 (чел./тыс. чел.)
=0-1,324=-1,324 (чел./тыс. чел.)
Коэффициент общего прироста населения:
![]() =-17,123+(-1,324)=-18,447
=-17,123+(-1,324)=-18,447
Специальный коэффициент рождаемости:
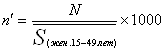 =1000*0,8/(430,4*0,39)= 4,766
=1000*0,8/(430,4*0,39)= 4,766
Тема 10
Задача 1
Имеются данные на конец года по РФ, млн. чел.:
- численность населения – 146,7
- экономически активное население – 66,7
- безработных, всего - 8,9, в том числе
зарегистрированных в службе занятости – 1,93.
Определить: 1) уровень экономически активного населения; 2) уровень занятости; 3) уровень безработицы; 4) уровень зарегистрированных безработных; 5) коэффициент нагрузки на 1 занятого в экономике.
Решение:
Коэффициент экономически активного населения:
![]() =66,7/146,7=0,45467=45,467%
=66,7/146,7=0,45467=45,467%
Коэффициент занятости
![]() :
:
занятые = экономически активные - безработные =66,7-8,9=57,8 млн. чел.
![]() =57,8/66,7=0,8666=86,66%
=57,8/66,7=0,8666=86,66%
Коэффициент безработицы:
![]() =8,9/66,7=0,1334=13,34%
=8,9/66,7=0,1334=13,34%
Уровень зарегистрированных безработных:
зарегистрированные в службе занятости / экономически активные=1,93/66,7 = 0,0289=2,89%
Коэффициент нагрузки на одного занятого в экономике – это число незанятых в экономике, приходящееся на одного занятого:
S - численность населения.
![]() = (146,7-57,8)/57,8=1,538
= (146,7-57,8)/57,8=1,538
Похожие работы
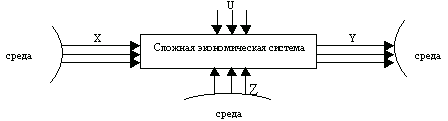
... системы. При этом очень важно учесть все, что имеет значение для той практической задачи, в которой возникла потребность в кибернетическом моделировании, и вместе с тем не переусложнить систему. Следующим этапом является составление математических моделей эффективного функционирования объекта и его системной модели. Затем производится программирование описания и моделей его функционирования. ...
... ai- расход сырья на единицу продукции; B - общий запас сырья; W - область допустимых ограничений; Тема 2. Метод математического моделирования в экономике. 2.1. Понятие “модель” и “моделирование”. С понятием “моделирование экономических систем” (а также математических и др.) связаны два класса задач: 1) задачи анализа, когда система подвергается глубокому изучению ее ...
... а это предполагает, что содержание наиболее предпочтительно критерия оптимальности ориентировано на максимизацию прибыли. 1.3 Методики моделирования программы развития сельскохозяйственного предприятия в работах ученых экономистов В экономических исследованиях издавна применялись простейшие математические методы. В хозяйственной жизни широко используются геометрические формулы. Так, площадь ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...

0 комментариев